1. 개요
투 포인터 알고리즘은 리스트에 순차적으로 접근해야 할 때, 2개의 점의 위치를 기록하면서 처리하는 알고리즘이다.
예를 들어 한 반에 학생이 40명이 있을 때, 모든 학생을 번호 순서대로 일렬로 세운 뒤에 학생들을 순차적으로 지목한다고 하자
2,3,4,5,6,7번 학생을 지목해야할 때, 우리는 번호로 한명씩 부르기보다는, "2번부터 7번까지의 학생"이라고 부를 수도 있다.
이처럼 리스트에 담긴 데이터에 순차적으로 접근해야 할 때는, '시작점'과 '끝점' 2개의 점으로 접근할 데이터의 범위를 표현할 수 있다.
2. 예시 - 특정한 합을 가지는 부분 연속 수열 찾기 문제
양의 정수로만 구성된 리스트가 주어질때, 그 부분 연속 수열중에서 특정한 합을 갖는 수열의 개수를 출력하는 문제를 생각해보자.
예를 들어 1,2,3,2,5를 차례대로 원소로 갖는 리스트가 주어져 있다면
합이 5인 부분 연속 수열은 몇개나 존재할까?
2,3
3,2
5
위와 같이 3개만 존재한다.
3. 알고리즘
투 포인터 알고리즘의 특징은 2개의 변수를 이용해 리스트 상의 위치를 기록한다는 점이다.
"특정한 합을 가지는 부분 연속 수열 찾기" 문제에서는 부분 연속 수열의 시작점(start)과 끝점(end)의 위치를 기록한다.
특정한 부분합을 M이라고 하자.
1) 시작점과 끝점이 첫번째 원소의 인덱스인 0을 가리키도록 한다.
2) 현재 부분합이 M과 같다면 카운트 한다.
3) 현재 부분합이 M보다 작으면 end를 1 증가시킨다.
4) 현재 부분합이 M보다 크거나 같으면 start를 1 증가시킨다.
5) 모든 경우를 확인할 때까지 2)~4)를 반복한다.
4. 예시를 통해 이해하는 투포인터 알고리즘
수열 1,2,3,2,5에서 합이 5인 부분 연속 수열은 몇개나 있는지 찾아보자.

초기 단계에서는 시작점과 끝점이 첫번째 원소의 인덱스를 가리키도록 한다
이 때 s~e의 부분합은 1이므로 카운트하지 않는다.

부분합이 1로 원하는 5보다 작기때문에, 이러한 부분수열에 양의 정수를 하나 더 포함시켜야 부분합이 1에서 5에 가까워질 것이다.
그러므로 end를 1 증가시켜서 수열을 하나 더 포함시킨다

그래도 부분합이 3으로 5보다 작으므로, 다시 end를 1증가시켜서 하나의 수를 더 포함시킨다

이런 경우, 부분합은 6으로 이제는 원하는 5보다 커졌다. 그래서 수열에 포함된 양의 정수 하나를 제거해줘서,
부분합을 작게 만들어줘야한다. start를 1 증가시키면, 부분 수열에서 수 하나가 빠져나간다

이 경우 2,3은 부분합이 5이므로 원하는 5와 같으니 카운트를 한다.
그리고 부분합이 원하는 값보다 크거나 같으면 start를 1 증가시킨다.
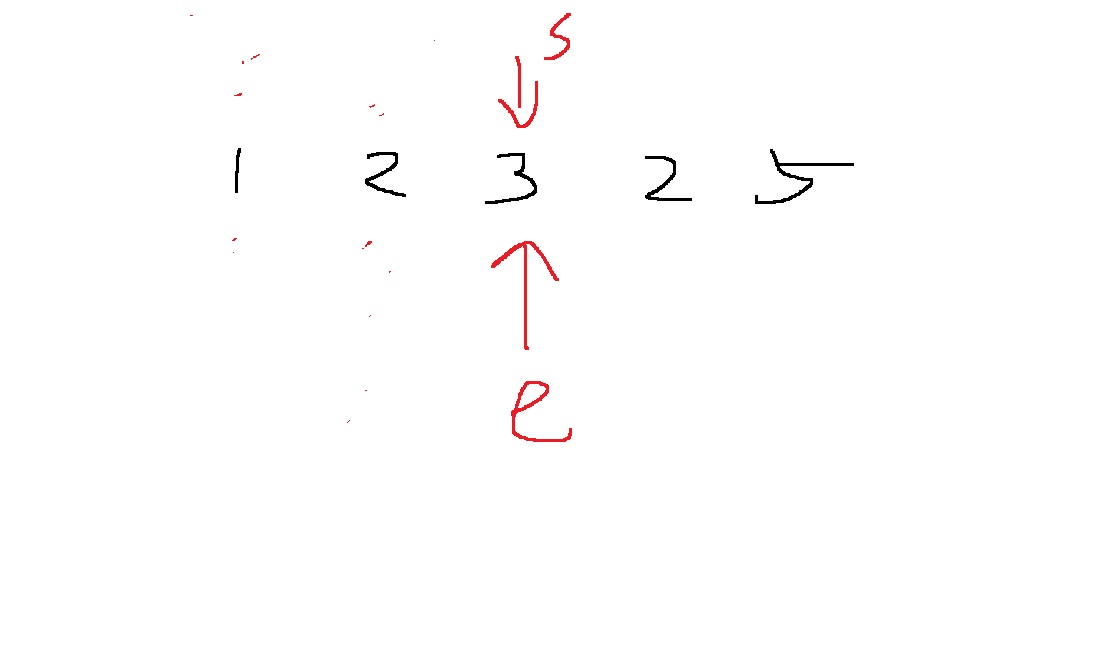
이 경우, 부분합은 3이므로 end를 1 증가시켜서 수 하나를 더 포함시키자
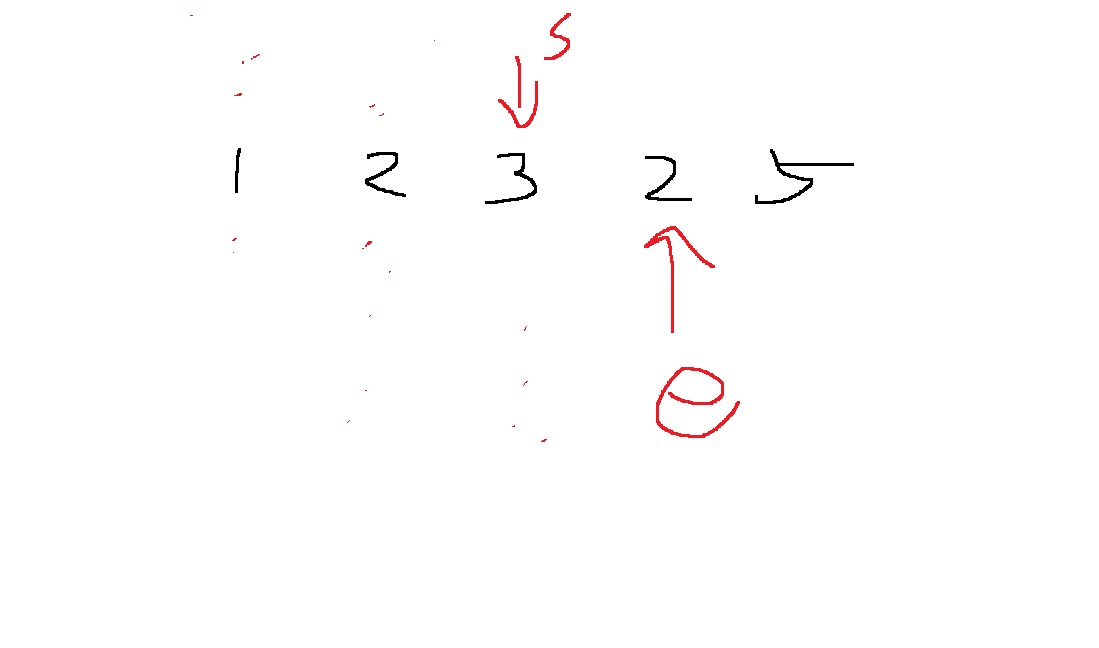
이 경우 부분합은 5이므로 원하는 합과 같으니 카운트 한다.
부분합과 원하는 합이 같으면 start를 1 증가시킨다
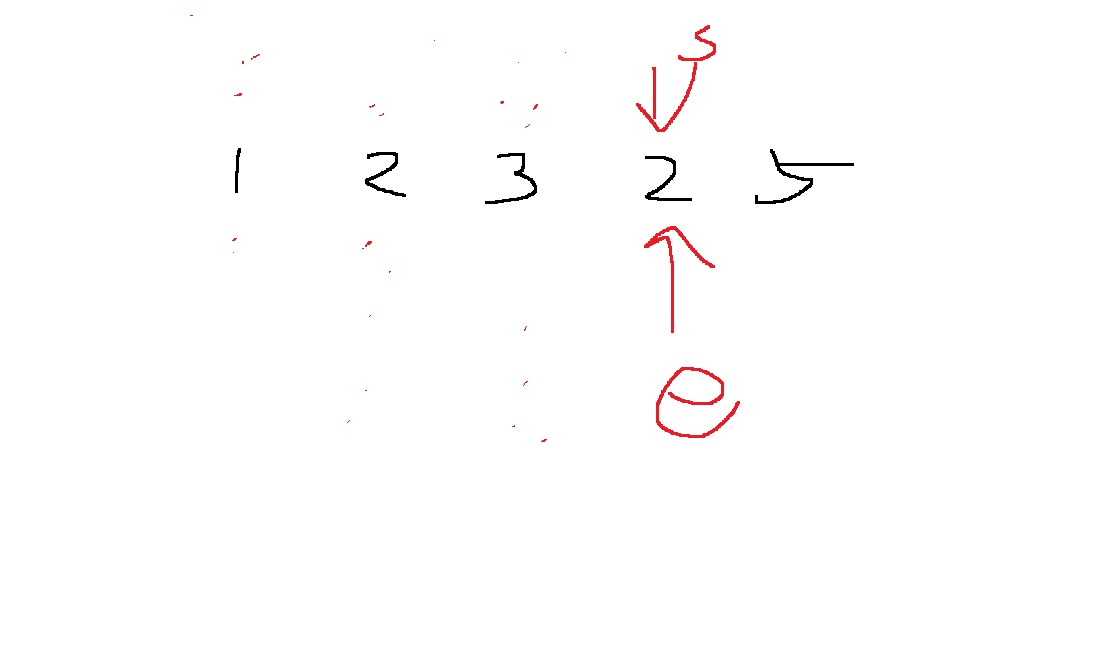
이 경우 부분합은 2로 원하는 합보다 작으니 end를 1 증가시킨다.
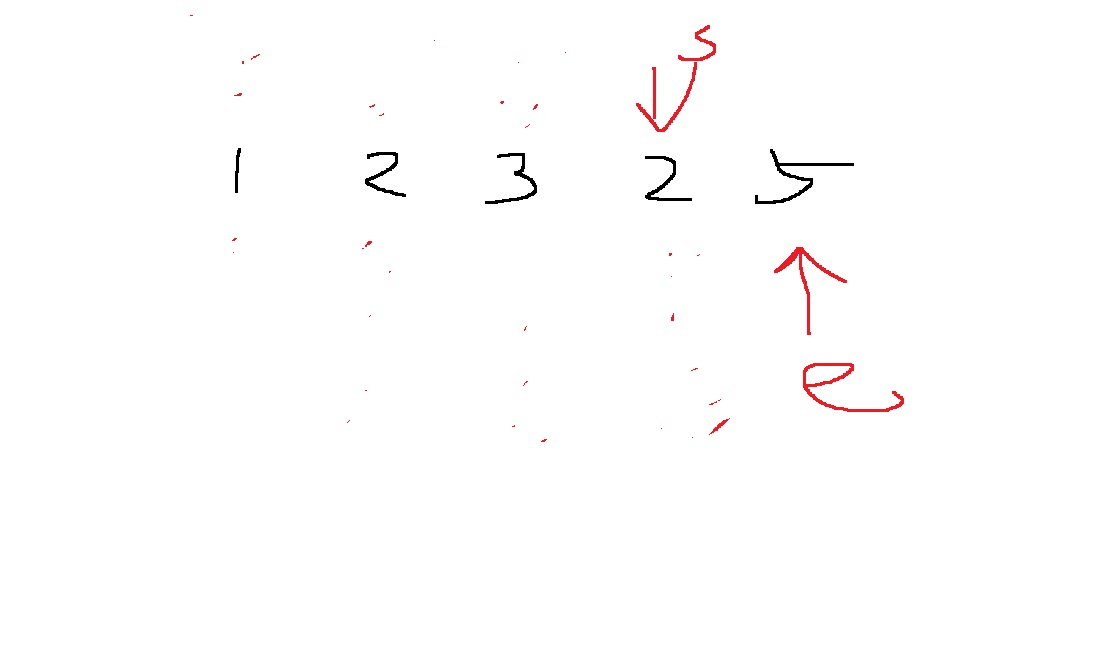
이러면 부분합은 7로 원하는 합보다 커졌으니 start를 1 증가시킨다

이 경우, 부분합은 5이니 카운트 한다. 더 이상 이동할 수 없으니 종료한다.
이렇게 풀이가 가능한 이유는, 모든 정수가 양의 정수이기 때문에, 시작점을 오른쪽으로 이동시키면 항상 합이 감소하고
끝점을 오른쪽으로 이동시키면 항상 합이 증가하기 때문이다.
그래서 리스트의 원소가 하나라도 음수가 있다면 적용시킬 수 없다.
5. 연습문제
2003번: 수들의 합 2
첫째 줄에 N(1 ≤ N ≤ 10,000), M(1 ≤ M ≤ 300,000,000)이 주어진다. 다음 줄에는 A[1], A[2], …, A[N]이 공백으로 분리되어 주어진다. 각각의 A[x]는 30,000을 넘지 않는 자연수이다.
www.acmicpc.net
위에서 설명하는 특정한 합을 가지는 연속 부분 수열의 개수를 구하는 문제
6. 풀이
위 알고리즘 그대로 구현해봤다
당연히 인덱싱은 사용하지 않는다
사용한다면 아무 의미가 없거든
시작점과 끝점을 명시하고, 누적합 변수 sum_value를 변화시킨다
end를 1 증가시킨다는 것은, 1 증가 후에 증가된 곳의 원소를 더해준다는 뜻
start를 1 증가시킨다는 것은, 증가 이전에 원소를 빼주고, start를 1 증가시킨다는 뜻
start가 배열의 범위를 벗어나기 이전에, end가 배열의 범위를 벗어난다면 모든 경우를 다 조사한 것이다
start가 배열의 범위를 벗어나서 n이 될 수는 있는데, 인덱싱 에러는 일어나지 않는다
하지만 start가 n이 된다면... end는 n-1이고 합이 0이라 end를 1 증가시켜 n이 될거임
그러면 end는 인덱싱 에러 가능성이 있어서.. end가 n이상이면 반복문을 탈출하고 종료한다
from sys import stdin
n,m = map(int,stdin.readline().split())
num_list = list(map(int,stdin.readline().split()))
#시작점과 끝점 포인터
s = 0
e = 0
#최초 부분수열의 합
sum_value = num_list[0]
cnt = 0
while 1:
#만약 누적합이 m과 같다면...
if sum_value == m:
#카운팅을 하고
cnt += 1
#s를 1 증가시킨다
#1 증가시킨다는 것은 증가 이전에 원소를 누적합에서 빼준다는 뜻
sum_value -= num_list[s]
s += 1
#만약 누적합이 m보다 크다면...
elif sum_value > m:
#s를 1 증가시킨다
#1 증가시킨다는 것은 증가 이전에 원소를 누적합에서 빼준다
sum_value -= num_list[s]
s += 1
#만약 누적합이 m보다 작다면...
else:
#end를 1 증가시킨다.
e += 1
#만약 end가 n 이상으로 배열 범위를 벗어난다면
#더 이상 조사할 수열이 없다는 뜻이다.
if e >= n:
break #반복문을 탈출
#범위를 벗어난 것이 아니라면, end의 원소를 누적합해준다.
sum_value += num_list[e]
#반복문을 탈출하면 수열 개수를 출력
print(cnt)
7. 다른 풀이
공부하는 책에서 제시하는 모범 답안을 보자
시작점을 반복문을 이용해서 증가시키고, 증가할때마다 끝점을 그에 맞게 증가시키는 방식
from sys import stdin
#데이터의 개수 n, 원하는 합 m
n,m = map(int,stdin.readline().split())
#수열
num_list = list(map(int,stdin.readline().split()))
#필요한 변수
count = 0 #수열의 개수
interval_sum = 0 #누적 부분합
end = 0 #끝점 포인터
#시작점은 반복문을 돌면서 0~n-1로 증가시킨다
for start in range(n):
#end는 부분수열 합이 m보다 작으면 1 증가한다
#이때, end는 인덱스 최댓값인 n-1을 넘어가면 안된다
while interval_sum < m and end < n:
interval_sum += num_list[end]
end += 1
#반복문을 탈출했다면, end를 1 증가시킬 수 없음
#반복문을 탈출했다면, 부분합 interval_sum은 m이상임
#반복문을 탈출했다면, start를 1 증가시킬 차례임
#부분합이 m과 같다면 카운팅 1 증가
if interval_sum == m:
count += 1
#start를 1 증가시키기 이전에, 현재 start 원소를 빼주고 1을 증가
interval_sum -= num_list[start]
print(count)'알고리즘 > 투 포인터 알고리즘' 카테고리의 다른 글
| 겹치는 직선 구간쌍의 개수 빠르게 세기 (0) | 2024.08.02 |
|---|---|
| 투 포인터로 원소를 삭제하면서 가장 긴 수열을 찾을 수 있을까? (0) | 2023.06.08 |
| 투 포인터 올바르게 생각하기 기본문제로 연습2 (0) | 2023.04.12 |
| 투 포인터 기억해야할 점 - 끝 포인터를 처음으로 옮기지 않기 (0) | 2023.04.11 |
| 투 포인터 알고리즘 응용문제 배우기2 -정렬된 두 리스트의 합집합- (0) | 2022.10.30 |

