1. idea
I study math라는 입력문장을 unique한 단어들의 vocabulary로 변환하면 {‘I’, ‘study’,’math’}
사전의 각 단어는 vocab size만큼 차원을 갖는 one hot vector이다.
‘I’는 [1,0,0] ‘study’는 [0,1,0] ‘math’는 [0,0,1]
sliding window라는 기법은 한 단어를 중심으로 앞 뒤로 나타난 단어들과 (중심단어,주변단어) 입출력쌍을 구성하는 기법이다.

이 단어 쌍에서 중심단어를 input으로 두고 주변단어를 output으로 두는
예측 task를 수행하는 2-layer neural network를 구성한다.
one hot vector의 차원이 3차원이니 input과 output layer의 차원은 3차원
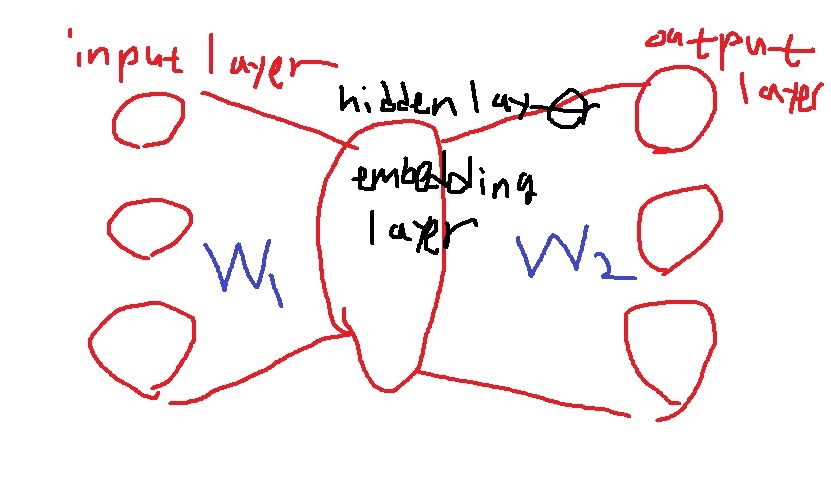
hidden layer의 차원 수는 사용자가 정하는 hyperparameter이다.
이 차원 수가 바로 word embedding vector의 차원수가 되는데 그래서 embedding layer라고도 부른다.
왜 embedding vector의 차원수가 되느냐?? 천천히 생각해보자.
이 네트워크의 학습과정을 알아보면 (study, math)에 대해서 예로 들어 생각해보자.
input으로 들어가는 study의 one hot vector인 [0,1,0]=X이고 output으로 나오는 math의 one hot vector는 [0,0,1]=Y이다.
W1이라는 linear transformation weight에 의해 X는 H=W1X가 되고
H에 대한 W2라는 linear transformation weight에 의해 W2H가 나온다.
이제 확률값으로 만들어주기 위해 softmax를 취하여
최종적으로 softmax(W2H)가 되는데 이로부터 가장 확률이 높은 차원에 1을 부여하고 나머지는 0으로 부여한다
우리는 이미 정답을 알고 있다. output이 Y=[0,0,1]이 되기를 원하므로 3번째 차원의 확률이 가장 높기를 원한다.
당연하지만 weight는 처음에는 적절하게 초기화시킨 값이므로 [0,0,1]로 안나올 수 있다.
그래서 예측한 softmax(W2H)와 실제 값 [0,0,1]의 차이로부터 loss function을 계산하고
이 값이 최소화가 되도록 W1,W2를 학습하는 것이다.
그럼 도대체 word의 embedding vector는 뭔데??? 최종적으로 학습한 결과로 얻은 W1과 W2의 열벡터가 바로 word의 embedding vector가 된다.
이런 이유에서 hidden layer의 차원수가 결국 embedding vector의 차원수가 된다고 말했다.
왜 embedding vector인지 연산의 특이점을 서술하면서 천천히 생각해보자.
2. Word2Vec 연산의 특징
먼저 첫번째 layer에서는 one hot vector는 0과 1로 구성되어있다는 특성상 1을 제외한 나머지는 모두 없애버리는 특징을 가지고 있다.

W1X의 결과는 W1의 2번째 열벡터를 가지고 온다.
이런 의미에서 W1,W2의 열벡터가 word의 embedding vector라는 것이다.
실제로 W1의 두번째 열을 가지고 오고 있는데 두번째 단어는 study이고 이것이 X라고 했고 one hot vector는 [0,1,0]이다.
위와 같은 연산의 특이한 점 때문에 실제로 구현할 때는 W1X의 행렬곱을 계산하지 않고
X의 1이 있는 index에 대응하는 W1의 열을 그대로 가져오는 연산으로 구현한다. 이게 더 효율적이니까
생각해보면 알겠지만 X가 vocab size만큼 차원을 가지므로 W1은 embedding layer의 크기 * vocab size의 크기 의 차원을 가진다.
W2는 vocab size의 크기 * embedding layer의 size의 차원을 가진다.
이런 의미에서도 W1,W2의 열이 vocab의 각 단어의 embedding vector가 될 수 있다는 것이다.
-----------------------------------------------------------------------------------------------------------------------------
2번째 연산을 자세히 살펴보도록 하자.

W2의 각 행과 W1X의 내적으로 W2H의 각 성분이 만들어진다.
W2H의 softmax를 취하면 확률값들이 나온다. 이것을 score vector라고 부른다.
당연하지만 W2H의 각 성분의 값이 클 수록 softmax(W2H)의 확률값도 커진다.
우리의 목표는 3번째 성분의 확률값이 가장 크게 만들어졌으면 하는 것이다. 그렇게 되도록 W1과 W2를 학습한다.
어떻게 하면 될까? 3번째 행과의 내적을 최대화시키며 나머지 행과의 내적은 최소화시키는 softmax loss를 이용하면 된다.
가장 이상적인 상황은 W2H의 3번째 성분은 무한대가 되고 나머지 두 성분은 음의 무한대가 되는 것.
그러면 softmax를 취하면 정확히 one hot vector가 나온다.
그래서 이 두 벡터의 차이를 나타낸 잘 알지만 log cross entropy를 주로 사용한다.
로그를 사용하는 이유는 보통 컴퓨터 계산을 위해 곱연산을 합연산으로 바꾸고 싶어서 그렇다.

이러한 cross entropy의 약점으로 y가 one hot vector라는 점에서 식이 간소화되는데
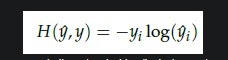
정답벡터만 고려하면 된다는 점임..
그러니까 W2의 3번째 성분과 W1X의 내적이 가장 크게, 나머지 두 성분과 W1X의 내적이 가장 작게 만들면 된다.
내적이 무엇이었을까? 벡터간 유사도를 측정한다.
이런 의미에서 W1, W2의 열이 embedding vector가 될수 있다는 것이다.
정답인 W2의 3번째 성분 embedding vector와의 내적 유사도를 가장 크게하고
나머지 오답인 1,2번째 성분 embedding vector와의 내적 유사도를 가장 작게한다는 것이다.
이렇게 각 vector간 유사도를 고려해서 학습하는 것이 Word2Vec의 핵심원리이다.
'딥러닝 > NLP' 카테고리의 다른 글
| Word2Vec의 2가지 형태 - CBOW와 skip-gram 모델 (0) | 2022.02.15 |
|---|---|
| text를 embedding시키는 Word2Vec의 성질 이해하기 (0) | 2022.02.11 |
| Word2Vec의 핵심 아이디어 (0) | 2022.02.05 |
| naive bayes classifier의 문제점을 보완하는 Laplace smoothing (0) | 2022.02.04 |
| Naive bayes classifier의 개념과 핵심 아이디어 (0) | 2022.01.30 |

