더블링(doubling, binary lifting, 희소배열,sparse table)에 대해 배우기

https://deepdata.tistory.com/972

희소 배열(sparse table) 자료 구조 배우기

 

희소 배열(sparse table)로도 알려진 더블링(doubling) 기법은 어떤 횟수 K를 2의 거듭제곱의 합으로 나눠서 생각하는 방법

 

모든 자연수는 2의 거듭제곱의 합으로 나타낼 수 있다.

 

7 = 4 + 2 + 1

 

10 = 8 + 2

 

25 = 16 + 8 + 1

 

즉 가장 가까운 2의 거듭제곱부터 빼면 감소하는 2의 거듭제곱의 수열의 합으로 나타낼 수 있다.

 

만약 횟수 K가 매우 크다면, 즉 $10^{9}$ 이상으로 O(K)에 불가능할 정도로 크다면, 더블링 기법을 반드시 생각해야한다.

 

반복 횟수 T를 이진수로 나타내서, 각 비트 K = 0,1,2,..logT에 대하여 비트마다 체크해서 비트 단위로 이동하면 된다는거

 

그러면 O(logT)에 해결할 수 있기 때문

 

https://atcoder.jp/contests/abc438/tasks/abc438_e

E - Heavy Buckets

 

 

N명의 사람과 N개의 양동이가 있다. 사람과 양동이 모두 1,2,,...,N번 번호가 매겨져 있다.

 

처음에 사람 i는 i번 양동이 하나만을 가지고 있고 모두 비어있다.

 

이제 다음 조작을 $10^{9}$번 반복한다.

 

i = 1,2,..,N에 대하여 모든 사람 i가 동시에 자신이 현재 가지고 있는 모든 양동이에 각각 i만큼 물을 추가하고,

 

그 양동이를 사람 A[i]번에게 건내준다

 

양동이에 담을 수 있는 물의 양은 무한하다고 가정한다.

 

i = 1,2,..,Q에 대하여 T[i]번째 조작이 끝나고 B[i]번 양동이에 들어있는 물의 양을 구하여라.

 

--------------------------------------------------------------------------------------------------------------------------

 

조작해야하는 횟수 K = 10^9로 매우 크기때문에, K번 모두 반복해보기에는 시간이 부족하다.

 

그래서 더블링 기법을 꼭 생각해야한다.

 

1) 사람 i에게 있던 양동이가 2^k초 후에 어떤 사람에게 있는지 dp1[k][i]

 

2) 사람 i에게 있던 양동이가 2^k초 후에 물이 얼마나 추가되어있는지 dp2[k][i]

 

먼저 초기화

 

1초 후에 사람 i는 A[i]에게 양동이를 넘겨주므로 dp1[0][i] = A[i]

 

1초 후에 사람 i는 양동이에 i만큼 물을 넣으므로 dp2[0][i] = i

 

이 초기값을 바탕으로 k = 1,2,3...을 채워넣는다.

 

$T = 10^{9}$이기 때문에 K = 0,1,2...,29까지 하면 충분하다. $2^{29} < 10^{9}$이기 때문에

 

$2^{k}$번 이동했다는 것은? $2^{k-1}$번 이동하고, 다시 $2^{k-1}$번 이동한 것과 같다.

 

예를 들어 k = 3인 경우 $2^{3} = 8$초 이동한 것은 $2^{2} = 4$초 이동하고, $2^{2} = 4$초 이동하는 것

 

그러면 dp1[k][i]는 어떻게 구할까?

 

i번 사람의 양동이가 $2^{k}$초 지나면 어디로 이동할까?

 

i번에서 $2^{k-1}$초 이동하고 dp1[k-1][i]번으로 보내고,

 

다시 여기서 $2^{k-1}$초 이동하여야하므로 dp1[k-1][dp1[k-1][i]]번으로 이동

 

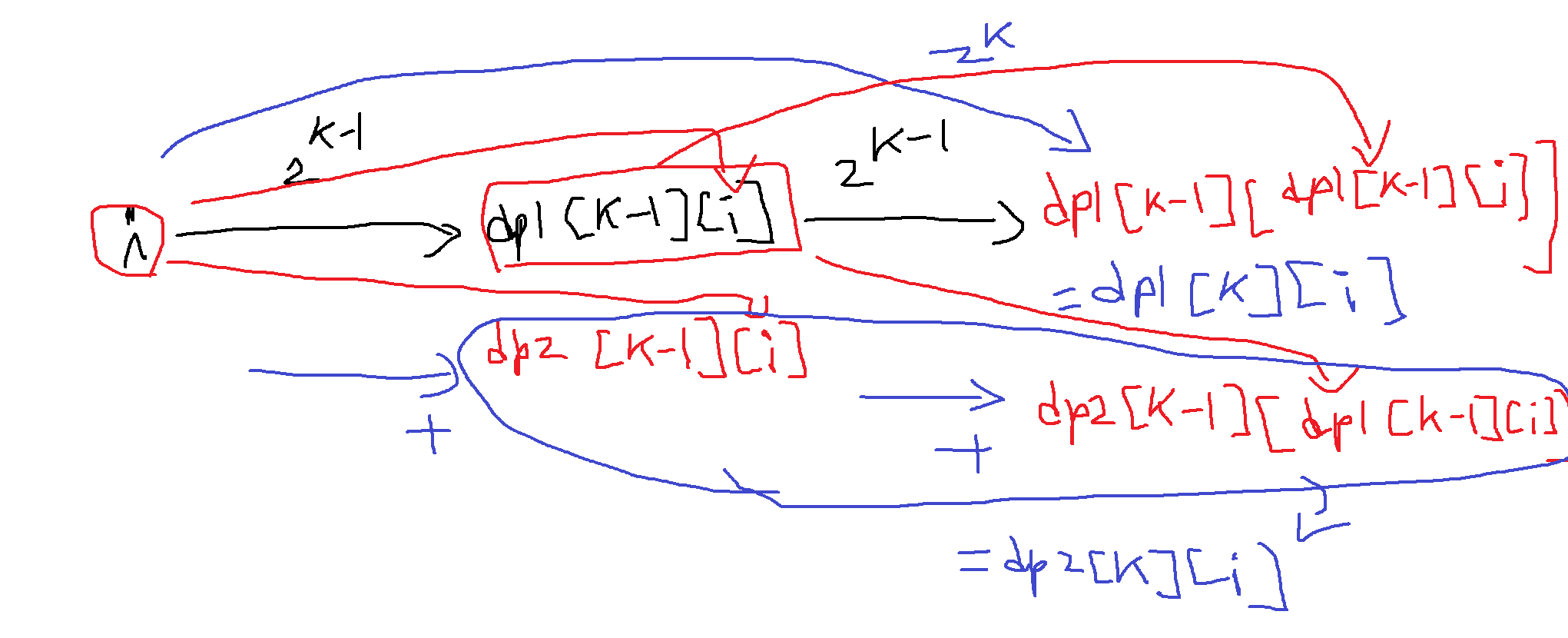
즉, dp1[k][i] = dp1[k-1][dp1[k-1][i]]

 

그러면 i번에서 $2^{k}$초 지난 후 양동이에 추가된 물 dp2[k][i]는 어떻게 구할까?

 

먼저 i번에서 $2^{k-1}$초 지나고 채워진 물 dp2[k-1][i]

 

이때 양동이는 dp1[k-1][i]에 있고, 여기서 $2^{k-1}$초 지나면 되므로

 

dp2[k-1][dp1[k-1][i]]

 

즉, dp2[k][i] = dp2[k-1][i] + dp2[k-1][dp1[k-1][i]]

 

 

 

 

 

 

그러면 문제는 T초 후에 양동이 B에 들어있는 물의 양을 구해야한다.

 

0초에 사람 B가 양동이 B를 가지고 있다.

 

T를 이진수의 합으로 나타내서 비트 단위로 점프를 함

 

구체적으로 T = 13이라면 13 = 1101(2)이다.

 

k = 0,1,2,3에 대하여 k번째 비트가 1인지 0인지 체크하고 1이라면 그것만큼 이동하면 된다.

 

k번째 비트에 대하여, $2^{k}$번 이동 한다면 현재 위치 curr에서 $2^{k}$초 이동 후 추가된 물의 양 dp2[k][curr]을 더해주고

 

curr에서 $2^{k}$초 이동 후 위치 curr = dp1[k][curr]로 이동 위치 갱신

 

n,q = map(int,input().split())

A = list(map(int,input().split()))

dp1 = [[0]*(n+1) for _ in range(30)]
dp2 = [[0]*(n+1) for _ in range(30)]

for i in range(n):
    
    dp1[0][i+1] = A[i]
    dp2[0][i+1] = i+1

for k in range(1,30):
    
    for i in range(1,n+1):
        
        dp1[k][i] = dp1[k-1][dp1[k-1][i]]
        dp2[k][i] = dp2[k-1][i] + dp2[k-1][dp1[k-1][i]]

for _ in range(q):
    
    t,b = map(int,input().split())

    m = t.bit_length()

    curr = b

    answer = 0

    for k in range(m):
        
        if t & (1 << k):
            
            answer += dp2[k][curr]
            curr = dp1[k][curr]
    
    print(answer)