https://atcoder.jp/contests/abc409/tasks/abc409_c
C - Equilateral Triangle
AtCoder is a programming contest site for anyone from beginners to experts. We hold weekly programming contests online.
atcoder.jp
원주의 길이가 L이고 점 1,2,3,..,N이 원 위에 찍혀있다.
i+1번째 점은 i번째 점에서 시계방향으로 di만큼 떨어져있다.
서로 다른 세 점 (a,b,c)를 고를때 이들이 정삼각형을 이루게 되는 그러한 (a,b,c)의 개수를 구한다.
-------------------------------------------------------------------------------------------------------------------------------------------
먼저 1번 점의 좌표를 0이라고 하자.
2번 점은 1번 점에서 d1만큼
3번 점은 2번 점에서 d2만큼 떨어져있으므로, 1번 점에서 d1+d2만큼
4번 점은 3번 점에서 d3만큼 떨어져있으므로, 2번 점에서 d2+d3만큼, 1번 점에서 d1+d2+d3만큼...
그러면 n번 점은 1번 점에서 d1+d2+...+dn-1만큼 떨어져있다.
따라서, di 배열의 prefix sum을 구해놓는다면 1,2,3,..,n번 점의 좌표를 O(N)에 구할 수 있다.
당연하지만 원주의 길이가 L이고 1번 점의 좌표를 0이라고 했으므로, i번 점의 좌표는 (d1+d2+...+di)를 L로 나눈 나머지를 구해야한다.
이제 각 점의 좌표를 모두 구했다면 정삼각형을 이루게 하는 세 점은 어떻게 찾을 수 있을까?
어떤 호 AB에 대하여 APB를 원주각이라고 부른다.
원의 중점 O에 대하여 호 AB와 연결된 AOB는 중심각이다.
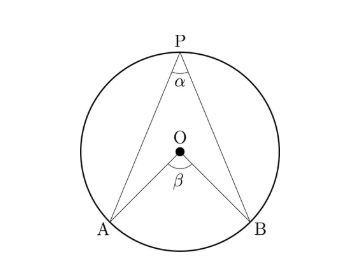
이때, 중심각은 원주각의 2배이다.
즉, 각 AOB = 각 APB * 2
호의 길이 $l = r * \theta$이므로, 호의 길이는 중심각에 비례한다.
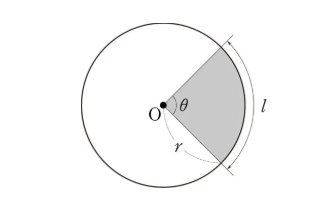
원에 내접하는 정삼각형은 원주각이 60'이고 중심각이 120'이다.
따라서, 세 점 ABC에 대하여 각 점이 서로 L//3씩 떨어져있다.
구체적으로 A의 좌표가 k라고 한다면 {A,B,C} = {k, k+L//3, k+2L//3}을 만족하는 k가 존재하면 된다.

그러므로 L이 3으로 나누어 떨어지지 않으면 애초에 정삼각형을 만들 수 없다.
L이 3으로 나누어 떨어진다면, 먼저 각 점 0,1,2,..,L에 대해 개수를 모두 구해놓고
k = 0,1,2,...,L//3-1에 대하여 k인 것의 개수 count[k]중 하나를 고르고
k+l//3인 것의 개수 count[k+l//3]중 하나를 고르고 k+2l//3인 것의 개수 count[k+2*l//3]중 하나를 고르면 정삼각형을 만드므로
count[k] * count[k+l//3] * count[k+2l//3]을 더해주면 된다.
n,l = map(int,input().split())
A = list(map(int,input().split()))
X = [0]
for i in range(1,len(A)):
A[i] += A[i-1]
for i in range(len(A)):
X.append(A[i] % l)
if l % 3 != 0:
print(0)
else:
count = [0]*(l+1)
for i in range(len(X)):
count[X[i]] += 1
x = l//3
answer = 0
for k in range(l//3):
answer += count[k] * count[k+l//3] * count[k+2*l//3]
print(answer)
'알고리즘 > 애드 혹 알고리즘' 카테고리의 다른 글
| 0이나 1을 뒤집어서 1이 연속인 구간이 최대 1개로 만들기 (0) | 2025.06.05 |
|---|---|
| 지뢰찾기 게임에서 지뢰의 최대 개수를 찾는 알고리즘 (0) | 2025.04.16 |
| 인접한 두 수를 분해하여 적절하게 바꿔서 정렬하는 방법 (0) | 2025.04.10 |
| 구간 내 가장 큰 해밍거리를 가지는 두 정수를 구하는 방법 (0) | 2025.04.08 |
| 야바위에서 바로 왼쪽이나 오른쪽으로 한번만 이동시킬 수 있을때 가능한 위치 구하기 (0) | 2025.03.26 |

