https://swexpertacademy.com/main/code/problem/problemDetail.do?contestProbId=AXTC3GH6D-EDFASe
SW Expert Academy
SW 프로그래밍 역량 강화에 도움이 되는 다양한 학습 컨텐츠를 확인하세요!
swexpertacademy.com
n개의 컵이 일렬로 늘어서있는데, 처음에 1번 컵에 공이 들어있다.
이 때 i번째 시행에서 ai번 컵과 bi번 컵을 서로 바꾼다.
임의의 시점에 정확히 한번, i번에 있는 공을 i-1번 컵이나 i+1번 컵으로 옮긴다.
전부 섞고 나서, 공이 있을 수 있는 모든 위치의 개수는?
----------------------------------------------------------------------------------------------------------------------------------------
컵에 1,2,3,...,n번 라벨을 붙인다고 생각해보자
6개의 컵이 있고 각 컵에 1,2,3,..,6번 라벨을 붙인다.

여기서 핵심은 a번 컵과 b번 컵을 바꿀때, 그 컵에 붙어있는 라벨은 바뀌지 않는다는 점이다.
3번 컵과 5번 컵을 자리를 바꾸면
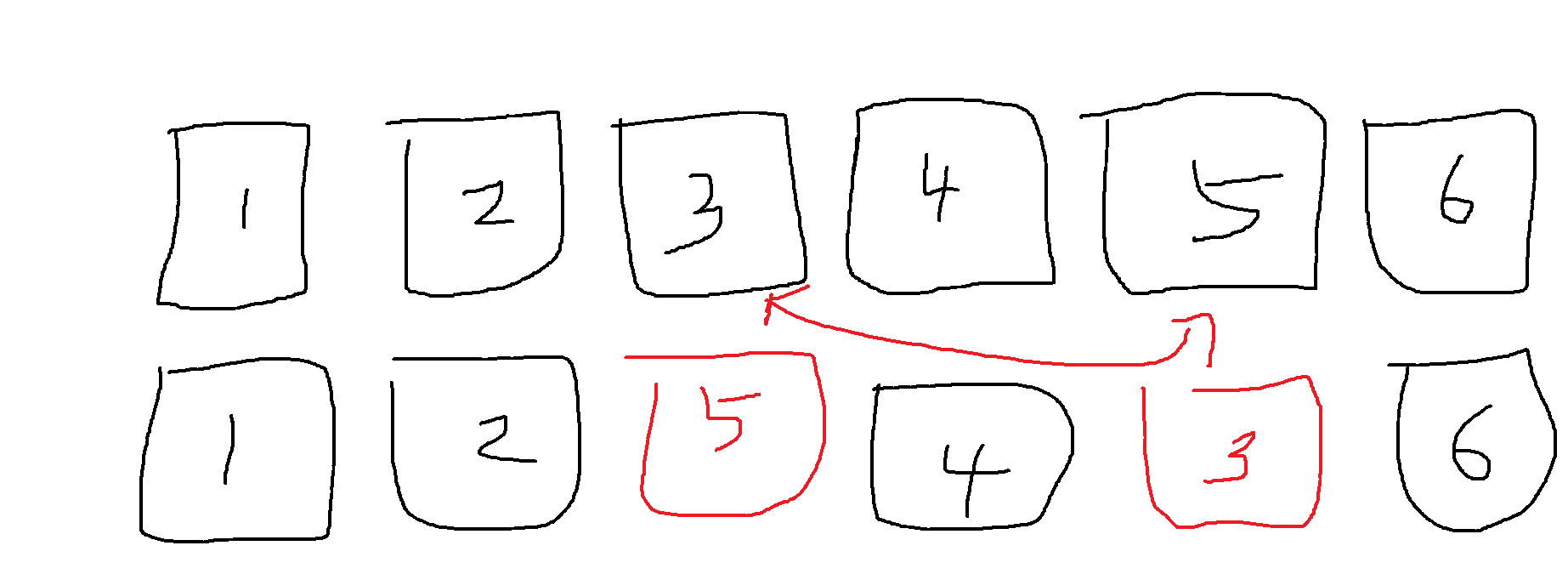
만약에 3번 컵에 공이 있었다고 가정하자.
3번 컵과 5번 컵을 바꾸고 나서 속임수를 쓴다면, 공이 있을 수 있는 위치는?
4번 컵과 6번 컵에 있을 수 있다.
이후에는 아무리 위치를 바꾸더라도, 공은 4번 컵 or 6번 컵 둘 중 하나에 있다는 것이 중요하다.
여기서 핵심은 컵에 붙은 라벨은 바뀌지 않는다는 것
컵의 위치를 바꾸면 각 라벨이 붙은 컵의 위치들이 바뀌겠지만, 이미 속임수를 썼기 때문에
이후에는 공은 어쨌든 4번이라고 라벨이 붙은 컵이나 6번이라고 라벨이 붙은 컵 둘 중 하나에 있을 수 밖에 없다.
원하는 정답은 "공이 있을 수 있는 컵의 위치를 정확히 찾는게 아니라 개수이기 때문"
그러므로 야바위를 하면서 a번 컵과 b번 컵을 서로 바꿀때마다, 공이 있는 위치를 알고 있다면
공이 있는 위치 바로 왼쪽, 바로 오른쪽을 기록해두면 그것들의 라벨 개수가 정답이 된다.
처음에 A = [1,2,3,..,N]이라고 하자.
여기서 1,2,3,..,N은 인덱스가 아니라, 컵에 붙은 라벨을 뜻한다고 생각하는 것이 중요하다.
now = 1로 하고, now - 1, now + 1 = 2을 정답 set에 넣어둔다
여기서 now값은 공이 있는 라벨을 말하는게 아니고 공이 있는 컵의 인덱스를 말하고 있다.
당연히 1~n번중 하나이므로 now-1 = 0은 안된다.
이후 a번 위치와 b번 위치를 바꾼다고 하자.
그러면 a번 위치의 라벨과 b번 위치의 라벨이 뒤바뀐다. A[a], A[b] = A[b], A[a]
공이 now = a번 위치에 있었다고 한다면, a번과 b번을 바꾸면 now = b번 위치에 있어야하고,
now = b번 위치에 있었다면, now = a번 위치로 바꿔줘야한다.
그러면 A[now]는 여전히 공이 있는 컵의 라벨을 말하고 있다.
여기서 속임수를 쓰면 공은 now-1번이나 now+1번으로 옮길 수 있고,
이후에는 공은 반드시 A[now-1]번 라벨 혹은 A[now+1]번 라벨에만 존재할 수 있으므로 이들을 정답 set에 넣어주면 된다.
T = int(input())
for t in range(1,T+1):
n,q = map(int,input().split())
A = list(range(n+1)) #일렬로 나열한 컵의 라벨 [0,1,2,3,..,n]
now = 1 #현재 공의 위치 1번
answer = set()
#0번 컵은 존재하지 않는다
if now-1 >= 1:
answer.add(A[now-1])
if now+1 <= n:
answer.add(A[now+1])
for _ in range(q):
a,b = map(int,input().split()) #a번과 b번을 바꾸는데
#원래 공이 a번에 있으면 b번으로 이동하고
if now == a:
now = b
#b번에 있으면 a번으로 이동하고
elif now == b:
now = a
#서로 바꿨으니 라벨도 바뀌어야함
A[a],A[b] = A[b],A[a]
#여기서 속임수를 쓰면
#공은 이후에는 A[now-1]번 라벨 혹은 A[now+1]번 라벨에만 존재할 수 있다
if now - 1 >= 1:
answer.add(A[now-1])
if now + 1 <= n:
answer.add(A[now+1])
print(f'#{t} {len(answer)}')
'알고리즘 > 애드 혹 알고리즘' 카테고리의 다른 글
| 인접한 두 수를 분해하여 적절하게 바꿔서 정렬하는 방법 (0) | 2025.04.10 |
|---|---|
| 구간 내 가장 큰 해밍거리를 가지는 두 정수를 구하는 방법 (0) | 2025.04.08 |
| 서로 순열이 되는 경우를 찾는 트릭(정렬해서 비교하기) (0) | 2025.03.05 |
| m개의 원소를 조건에 맞게 n개의 원소에 배치하는 방법 (0) | 2024.12.02 |
| 주어진 점들 중 최대 맨해튼 거리(Manhattan Distance)를 빠르게 찾는 방법 (0) | 2024.10.23 |

