총 n마리의 암소와 황소를 한줄로 세울때, 두 마리의 황소 사이에 최소 k마리의 암소가 있도록 줄을 세운다고 할 때,
그러한 방법의 수를 5000011로 나눈 나머지를 구한다.
이때 각 소는 구분할 수 없어서 서로 다르게 세워진 경우만 다른 경우의 수로 센다
n <= 10만이라 2차원 dp로 하기에는 메모리 초과가 날 가능성이 높고
2마리 황소 사이에 k마리 암소 세우고.. 어떻게 순열 돌리고 흠...
dp[i][j]를 i마리 소 세우는데 마지막에 황소가 오는 경우가 j = 0, 아닌 경우가 j = 1인데
마지막에 황소가 온다고 하더라도 그 전 정보를 알수가 없으니 이건 흠...
---------------------------------------------------------------------------------------------------------------------------------------------
dp[n] = n마리의 소를 세웠을 때 구하고자 하는 경우의 수
1) 처음에 세워진 소가 암소인 경우...
나머지 n-1마리로 조건에 맞게 세우기만 하면 되므로 dp[n-1]

2) 처음에 세워진 소가 황소인 경우
황소 옆에 k마리는 반드시 암소를 세워야하고, 그 뒤로 n-k-1마리는 조건에 맞게 세우기만 하면 되므로 dp[n-k-1]
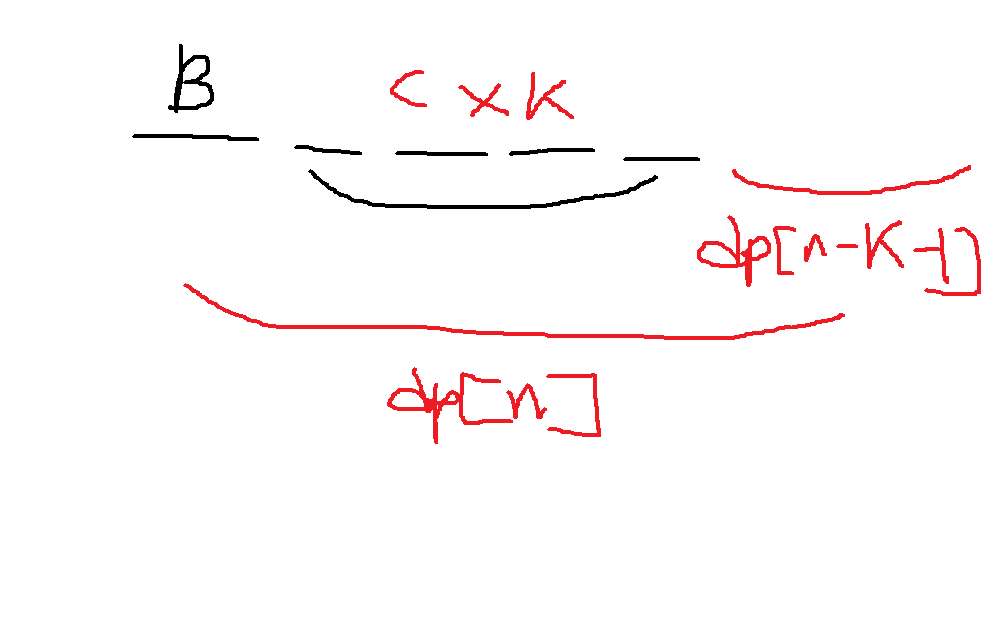
2가지 경우를 합한 dp[n] = dp[n-1] + dp[n-k-1]이다.
근데 n-k-1 < 0인 경우가 있을 수 있는데 무엇을 의미할까?
첫번째로 황소를 배치하는 경우, k마리 암소가 필요한데, 존재하는 소보다 k가 커서 불가능한 경우인데
예를 들어 n = 4이고 k = 10인 경우
세울 수 있는 방법은 BCCC으로 1가지가 가능하다는 말
그래서 n-k-1 < 0이면 dp[n-k-1] = 1
n = 0이면 아무것도 안하는 방법 dp[0] = 1로 1가지 있으므로...
dp[n] = dp[n-1] + dp[n-k-1], n-k-1 < 0이면, dp[n] = dp[n-1] + 1
n,k = map(int,input().split())
mod = 5000011
dp = [0]*(n+1)
dp[0] = 1
for i in range(1,n+1):
if i-k-1 < 0:
dp[i] = dp[i-1] + 1
else:
dp[i] = dp[i-1] + dp[i-k-1]
dp[i] %= mod
print(dp[n])
'알고리즘 > 다이나믹 프로그래밍' 카테고리의 다른 글
| 원형 배열에서의 다이나믹 프로그래밍 기본 (0) | 2024.12.24 |
|---|---|
| 최소 편집 거리(edit distance)를 구하는 알고리즘 (0) | 2024.12.11 |
| 정확히 배낭의 크기만큼 담아야하는 독특한 배낭 문제 (0) | 2024.10.01 |
| 선택한 원소의 인접한 원소는 선택할 수 없을 때 원소 합을 최대로 선택하는 방법 (0) | 2024.08.10 |
| 홀수 길이의 연속 부분 배열의 합 중 가장 큰 값을 구하는 방법 (0) | 2024.08.05 |

