neural network에서의 low rank approximation은 무엇이 있는가

1. filter decomposition

 

network의 filter를 decomposition하여 계산량을 줄이면서 decomposition하기 전의 결과에 approximation시키는 방법

 

depthwise separable convolution은 depthwise convolution을 수행하고 pointwise convolution을 수행하여

 

일반적인 convolution보다 계산량을 줄이고 원래 일반적인 convolution의 결과에 거의 approximation할 수 있다.. (같지 않나 아닌감)

 

일반적인 convolution과 depthwise separable convolution 계산량 비교

 

 

2. low rank tensor approximation

 

이미 학습된 network의 filter가 차원이 너무 높아 계산비용이 너무 많이 드는 경우

 

하지만 input을 받아 output을 내는 결과는 decomposition하기 전과 최대한 비슷하게 approximation

 

low rank tensor approximation을 활용하여 network decomposition 설명 그림

 

 

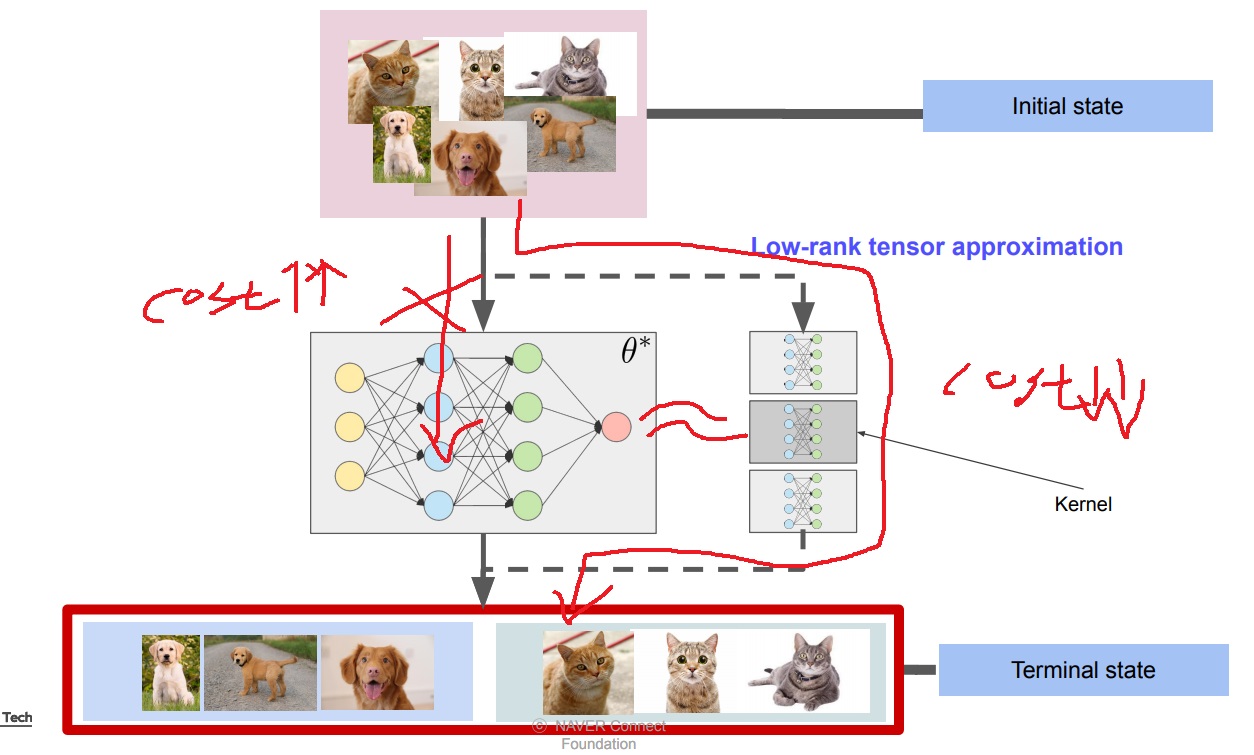
high rank의 network weight tensor를 low rank tensor의 곱이나 합으로 분해하여

 

그 중에 필요없는 tensor는 버리기도 하여 진짜 필요한 부분만 가지고 와서(truncated SVD같은 경우 0인 부분은 버려서 approximation시켰죠? 기억남?)

 

계산비용은 최대한 줄이면서 원래 결과와 최대한 비슷하게 approximation하는 방법

 

linear algebra의 tensor decomposition을 활용하여 학습된 filter tensor만 가지고 decomposition하여

 

모델을 경량화시키는 대표적인 data-free 방법이기도 함 (분해한 모델의 성능을 볼때는 데이터가 필요하지만)

 

 

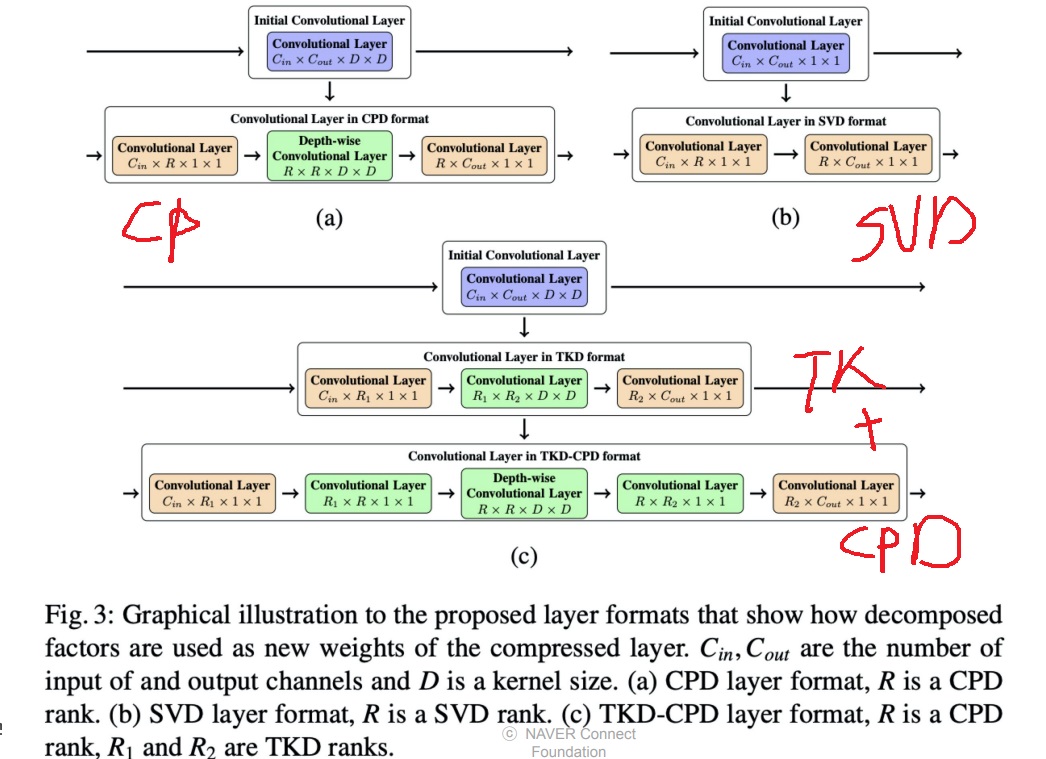
3. 구체적인 방법 예시 그림

 

network를 CP decomposition을 이용하여 layer의 weight를 분해할 수 있고

 

SVD를 활용하여 분해할 수 있고

 

Tucker decomposition을 수행한 다음에 CP decomposition을 수행할 수 있고

 

여러가지 low rank approximation 예시 그림