그래프에서 각 노드의 사이클까지 거리를 빠르게 구하는 놀라운 방법

1. 문제

 

정확히 하나의 사이클을 포함하는 무방향 연결 그래프(connected undirected graph)가 주어진다.

 

각 노드 번호가 0부터 n-1까지 n개의 노드를 가진다.

 

노드 a와 b 사이 거리가 a에서 b로 가기 위해 필요한 최소 간선의 수

 

노드 i = 0,1,2,..,n-1에서 이 그래프에 존재하는 사이클에 있는 임의의 노드까지의 최소 거리를 구한다면?

 

당연히 사이클에 포함된 노드는 사이클 까지의 거리가 0이다.

 

 

 

위 그래프는 1,2,3,4가 사이클을 이룬다.

 

1,2,3,4는 각각 사이클까지 거리가 0이고, 0번 노드는 사이클 까지 거리가 1

 

5번 노드는 사이클 까지 거리가 1, 6번 노드는 사이클 까지 거리가 2이다.

 

 

2. 풀이

 

사이클에 포함된 노드는  위상정렬에 포함되지 않는다는 점을 이용한다

 

 

 

무향그래프니까 진입차수(indegree)가 1인 노드를 먼저 큐에 모두 담는다.

 

위 그래프에서 0번 노드 6번 노드가 진입차수가 1이다.

 

q = [0,6]

 

이 노드를 제거하면서 다시 그래프에서 차수가 1인 노드를 큐에 담는다.

 

노드를 제거하는 과정에서 제거된 노드를 순서대로 다른 배열 seq에 담는다.

 

0번을 제거하면 seq = [0]이고 1번 노드의 진입차수가 원래 3인데 2로 줄었지만 1이 아니므로 큐에 담지 않는다.

 

여기서 핵심은 노드를 제거할때마다 인접 노드를 기록해둔다.

 

0번 노드를 제거하면서 인접 노드가 1번이므로 adj[0] = 1로 기록해둔다.

 

q = [6]

 

 

 

다시 6번 노드를 제거하면 이제 6번 노드가 진입차수가 1이되고 seq = [0,6], q = [5]

 

그리고 6번노드에 인접한 노드 5번을 기록해둔다 adj[6] = 5

 

 

 

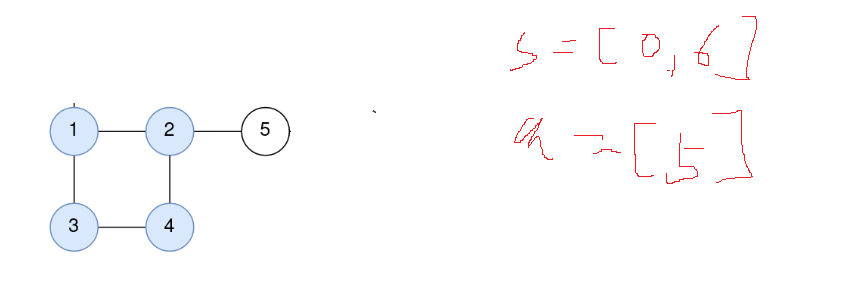
다시 5번 노드를 제거하면 s = [0,6,5]인데 2번 노드가 진입차수가 3인데 2로 줄었지만 1이 아니므로 큐에 담지 않는다.

 

이때 5번 노드에 인접한 노드 2번을 기록해둔다. adj[5] = 2

 

큐가 비면 위 과정을 종료한다.

 

이제 거리를 담은 배열 answer[i]는 노드 i에서 사이클까지 최소 거리를 나타낸다.

 

모두 0으로 초기화하고, s = [0,6,5]를 역방향으로 순회하여 각 노드 i번에 대해 인접한 노드 adj[j]를 이용하면...

 

각 노드 i번은 인접한 노드 adj[i]와의 거리가 1이므로

 

answer[i] = answer[adj[i]] + 1

 

s에는 사이클에 포함된 노드가 들어가있지 않으므로, 그러한 노드들은 answer값이 0이다.

 

따라서 s를 역방향으로 순회하면 사이클에서 가까운 노드부터 거리가 1씩 증가하게 된다.

 

이렇게 하면 시간복잡도 O(N)에 가능

 

from collections import deque

n = int(input())

graph = [set() for _ in range(n)]

for _ in range(n):
    
    a,b = map(int,input().split())
    graph[a].add(b)
    graph[b].add(a)
    
queue = deque([])

for i in range(n):
    
    if len(graph[i]) == 1:
        
        queue.append(i)
        
adj = [0]*n
s = []

while queue:
    
    i = queue.popleft()
    s.append(i)
    
    for j in graph[i]:
        
        adj[i] = j
        
        graph[j].remove(i)
        
        if len(graph[j]) == 1:
            
            queue.append(j)
        
    graph[i].pop()

answer = [0]*n

for i in s[::-1]:
    
    answer[i] = answer[adj[i]] + 1

print(*answer)

7
1 2
2 4
4 3
3 1
0 1
5 2
6 5
1 0 0 0 0 1 2

9
0 1
1 2
0 2
2 6
6 7
6 8
0 3
3 4
3 5
0 0 0 1 2 2 1 2 2

 

 

 

여기서 디테일은 graph = [set() for _ in range(n)]

 

set()으로 담아두면 위상정렬할 때

 

j번에 연결된 노드 i를 제거하고 싶을 때 graph[j].remove(i) 으로 O(1)에 제거가능