1. bit와 byte
1bit는 2가지 경우를 표현하는 정보의 단위로 0 아니면 1을 표현한다
1byte는 8bit와 같으며 몇가지를 표현할 수 있을까?
1bit가 2가지를 표현하므로 $2^{8}$가지를 표현할 수 있다
보통 자주 언급되는 bit가 정수를 어디까지 표현할 수 있을까??
1bit가 0 아니면 1을 표현하므로 0부터 $2^{1} - 1$까지 표현한다고 말한다
2bit는 $2^{2}$가지를 표현하므로 0,1,2,3의 4가지를 생각하여 0부터 $2^{2} - 1$까지 표현한다고 말한다
비슷하게 1byte=8bit는 0부터 $2^{8} - 1$까지 음이 아닌 정수를 표현할 수 있다
음수를 포함하겠다면? 0부터 255까지 256가지를 절반으로 나눠서 128가지씩 나눠가져서
–128부터 127까지 표현 (n bit인 경우 $-2^{n-1}, 2^{n-1}-1$까지 표현)할 수 있을 것이다
2. single precision
floating point를 32bit로 표현하면 single precision이라 말하고 64bit로 표현하면 double precision이라 말한다.
물론 그 이상도 있다(128bit,....)
floating point를 표현하는 방법은 여러 가지가 있지만 대부분 IEEE754 방법을 사용한다
아이디어는 $-3.14 = -1 * 0.314 * 10^{2}$으로 나타낼 수 있다는 것에 기초하여
모든 실수를 부호(sign), 가수(fraction), 지수(exponent)만 있으면 표현할 수 있다는 것이다.
floating point를 32bit로 표현하기 위해서는 1bit는 sign(부호) 8bit는 exponent, 23bit는 mantissa(fraction)를 사용한다.
10진법, 2진법 다 생각할 수 있는데 컴퓨터는 2진법을 사용하니 보통 2진법으로 정의함

여기서 $b_{i} = 0 또는 1, i = 0,1,2,..,31$
참고로 64bit는 1bit는 sign, 11bit는 exponent, 52bit는 fraction으로 저장
3. 2진수 소수점은 어떻게 옮길까??
예를 들어 10진법 수인 21.8125를 생각해보자.
21과 0.8125의 합으로 생각할 수 있다.
21을 2진법으로 표현하면... 21을 2로 계속 나눠가면서 나머지를 구한 뒤 아래서부터 위로 올라오면서 나머지만 가져오면 나타낼 수 있다.
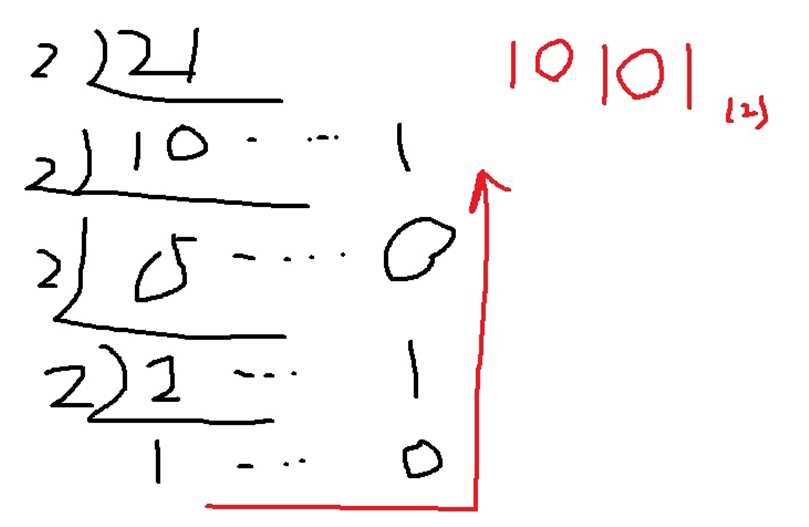
소수인 0.8125는 2진법으로 어떻게 나타낼까?
소수에 2를 곱하면서 1을 넘어가면 그 1을 가져오고 그렇지 않으면 0을 가져와 최종적으로 1이 될 때까지 진행하여 위에서부터 가져옴

그래서 21.8125는 $10101_{2}$와 $0.1101_{2}$의 합인 $10101.1101_{2}$로 나타낼 수 있다.
소수점을 옮기는 것에 대해 생각해보자.
10진법의 소수인 0.8125는 10을 곱하면 8.125이고 또 10을 곱하면 81.25이고 또 10을 곱하면 812.5로 10을 곱하면서 소수점을 옮길 수 있다.
이것이 왜 가능하냐면 $0.8125 = \frac{8}{10} + \frac{1}{10^{2}} + \frac{2}{10^{3}} + \frac{5}{10^{4}}$ 로 나타낼 수 있는데 10을 양변에 곱하면
$8.125 = 8 + \frac{1}{10^{1}} + \frac{2}{10^{2}} + \frac{5}{10^{3}}$
비슷하게 10을 또 양변에 곱하면 $81.25 = 80 + 1 + \frac{2}{10^{1}} + \frac{5}{10^{2}}$
비슷하게 $0.1101_{2} = \frac{1}{2} + \frac{1}{2^{2}} + \frac{0}{2^{3}} + \frac{1}{2^{4}}$에서 2를 곱하면
$0.1101_{2} * 2 = 1 + \frac{1}{2^{1}} + \frac{0}{2^{2}} + \frac{1}{2^{3}}$
우변이 나타내는 수치는 $1.101_{2}$라는 것을 쉽게 생각할 수 있다.
그러므로 $0.1101_{2} * 2 = 1.101_{2}$
그러니까 2의 거듭제곱으로 2진수 소수점을 옮길 수 있다는 뜻이다.
4. 예시로 이해하는 single precision 표현법
위에서 설명한 소수점을 옮기는 방법을 생각하면
10진수 실수인 21.8125는 $10101.1101_{2} = 2^{5} * 0.101011101_{2}$
위에서 정의한 IEEE754 표현법을 이용하여 조금 더 멋있게 표현해보자면
$21.8125 = (-1)^{0} * 2^{5} * 0.101011101_{2}$
그런데 컴퓨터는 5를 5라고 저장하지는 않는다...
그리고 특수한 이유(뒤에서 설명)로 127을 더해서 이 5는 132를 2진수로 나타내면 $10000100_{2}$이므로
최종적으로 sign부분을 $0_{2}$, 지수 부분을 $10000100_{2}$ 가수 부분을 $0.101011101_{2}$으로 저장
실제로 이것을 32bit로 표현하면 $0_{2}10000100_{2}10101110100000...._{2}$으로 표현한다고 함 ( (2)는 그냥 구분하기 위해 사용함)
(지수부분은 앞에 비어있는 곳을 0으로 채우고 가수부분은 뒤에 비어있는 곳을 0으로 채우는 듯?)
추가적으로 가수부의 최상위 비트는 1로 만드는 normalize하는 경우가 보통이라고 함
$21.8125 = (-1)^{0} * 2^{5} * 0.101011101_{2}$ 이렇게 나타냈지만
보통은 $21.8125 = (-1)^{0} * 2^{4} * 1.01011101_{2}$ 이렇게
참고로 지수부는 127을 더한 뒤에 저장하는 이유 중 하나는 음수의 경우 음수 부호를 비트로 저장하지 않기 위해서 127을 더해 양수로 바꿔 저장하는 것
5. bias exponent
그런데 위에서 표현식 $(-1)^{sign} * 2^{exponent - 127} * (1.b_{22}b_{21}...b_{0})$라고 나타나있다
지수부분에 왜 127을 뺐는지 궁금할 수 있는데 ‘biased form’이라고 부른다
Biasing is done because exponents have to be signed values in order to be able to represent both tiny and huge values, but two's complement, the usual representation for signed values, would make comparison harder.
exponent가 큰 수와 작은 수를 표현하기 위해 signed value를 가질 수 있다고 하는데
8bit 정수 표현은 –127~128까지 가능하다는 것을 표현하는 것 같다
그런데 2의 거듭제곱을 이렇게 표현하면 큰 수와 작은 수에 대한 비교가 어렵다는 설명
To solve this problem the exponent is stored as an unsigned value which is suitable for comparison, and when being interpreted it is converted into an exponent within a signed range by subtracting the bias.
그래서 exponent를 0~255까지 저장하게 만들고 여기에 bias 항인 127을 빼면
exponent가 126이하이면 2의 거듭제곱 부호가 음수여서 소수점이 앞으로 옮겨지면서 작은 수를 표현하고 < 111.110111001에 2^-2를 곱하면? >>>>> 1.11110111001 >
exponent가 128이상이면 2의 거듭제곱 부호가 양수여서 소수점이 뒤로 옮겨지면서 큰 수를 표현할 수 있다는 설명 < 111.110111001에 2^2를 곱하면? >>> 11111.0111001 >
6. special case
만약 exponent가 0이라면 어떨까?
$(-1)^{sign} * 2^{-127} * (1.b_{22}b_{21}...b_{0})$ 혹은 가수부의 1을 2로 표현하면
$(-1)^{sign} * 2^{-126} * (0.b_{22}b_{21}...b_{0})$
중요한 것은 $2^{-126}$이 곱해지면서 전체 수가 0에 매우 가까워진다는 뜻이다.
실제로 0이 아니더라도 많은 경우 performance issue를 일으키므로(denormal number) 그냥 0으로 처리하도록 약속을 한다. (보통 underflow라고 부름)
반대로 exponent가 255라면?
$(-1)^{sign} * 2^{129} * (0.b_{22}b_{21}...b_{0})$인데 가수부의 $(0.b_{22}b_{21}...b_{0})$이 0에 가깝더라도
$(-1)^{sign} * 2^{129}$가 너무 커서 $\infty$나 -$\infty$에 가까워진다. (overflow라고 보통 부름)
당연히 가수부가 0에 가깝지 않으면 $\infty$나 -$\infty$에 가까워지는 것
(특별히 이 경우는 무한대보다는 Not a number, NaN이라고 함, 혹은 불가능한 연산인 0으로 나누는 연산의 경우)은 두말할 필요도 없다
그래서 exponent가 255인 경우는 $\infty$나 -$\infty$으로 예약되어있다.
최종적으로 평범한? 수는 exponent에는 1부터 254까지 사용하고 0인 경우는 0으로 처리하고 255인 경우는 sign에 따라
$\infty$나 -$\infty$ 혹은 NaN으로 처리
7. 정확도 문제
floating point 표현은 저장하는 bit수의 한계로 인해 원하는 실수를 사실 정확히 표현하지는 못한다
0.1이라는 간단한 실수만 해도 (조금만 생각해보면) 2진수로 나타내면 무한소수로 나타난다
그래서 대부분의 경우 실제 실수값과 컴퓨팅 연산은 어느정도 오차가 생김
예를 들어 24비트 단정밀도 표현에서, 십진수 0.1은 지수 = -4; 가수 = 110011001100110011001101 이고 그 값은 정확히 0.1000000014901161193847656256이다.
그로 인해 기본적인 연산법칙인 결합법칙, 분배법칙이 항상 성립하지는 않으며
수학적으로 계산 결과가 같아야하는데 약간 차이가 생기는 여러 가지 문제점들이 발생하기도 한다
8. low precision training은 왜 등장했는가
32bit single precision의 경우 실수 하나만 저장하는데도 메모리에 32bit나 필요하다.
거의 대부분 하드웨어가 이런 연산이 가능하나 항상 가능한 것은 아님
machine learning training은 실제 세상에서 데이터를 모을 때 생기는 imprecision과 SGD같은 알고리즘에 의한 random sampling으로 인해 이미 noisy하다고 표현한다
bit수를 줄이면 당연히 실수 표현의 정확도는 떨어지겠지만 이 정도 영향력이
“”“실제 세상에서 데이터를 모을 때 생기는 imprecision과 SGD같은 알고리즘에 의한 random sampling”“”에 의한 영향력에
비해 너무나도 작기 때문에 성능에 큰 영향을 미치지 않는다는 것이다.
수치에 bit수를 줄여서 저장하고 표현함으로써 메모리를 어느정도 아끼고 속도를 조금 얻으며
성능은 그렇게 손해보지 않는(당연히 어느정도 손해는 보겠지만) 방식이 low precision training이다.
9. half precision
machine learning에서 트렌드를 주도하는? 표현 방식은 16bit half precision 표현법이다.

어떤 특징을 가지는가? 당연히 single precision에 비해 실수에 대한 오차는 더 클 것이고
overflow의 한계치는 더 작을 것이고(overflow가 빈번하게 일어남)
underflow의 한계치는 더 클 것이다(underflow가 빈번하게 일어남)

만약 machine learning training 중 half precision의 overflow와 underflow의 한계치 내에서 수치를 다룬다면 half precision을 사용하는 것이 분명 이점을 가진다.
그 외에 생각해볼 수 있는 이점은 너무나도 명확하다.
메모리에 수치를 더 많이 저장할 수 있고 시간당 전송되는 수치도 더 많고 에너지 소비량도 적고 병렬처리도 빠름
반대로 안좋은 점은
위에서 설명한대로 overflow와 underflow 한계치가 더 좁다는 것,
single precision number를 half precision으로 나타낼 때 quantization error로 더 큰 error가 발생함
그리고 16bit 연산을 지원하는 hardware가 있어야함
10. 단점을 극복하기 위한 시도들
1) 한계치가 더 좁다는 단점을 극복하기 위해 지수부의 bit수를 늘리거나

2) 16bit 연산을 지원하는 hardware가 있어야한다는 단점을 극복하기 위해 fixed-point arithmetic을 사용하기도 한다고함

정수로 근사시켜서 모든 걸 표현하나봄??
정수로 계산하는 것은 계산비용이 훨씬 덜 들고 이미 많은 경우 machine learning에서 8bit fixed point number를 사용한다고 함
3) quantization error가 발생할 수 있다는 단점을 극복하기 위해 stochastic rounding을 사용한다고 함
일반적으로 floating point 연산에서 근사치를 구할 때 표현하는 수에 최대한 가까운 수로 반올림? 버림? 올림? <rounding>을 함
그런데 machine learning의 많은 경우 이러한 접근이 좋은 접근은 아니다.
특히나 평균을 구할 때 rounding을 하고나서 평균을 구하는 것과 rounding을 하기 전에 평균을 구하는 것은 분명한 차이가 있음
무슨 말이냐면 통계적으로도 rounding을 하고 나서는 사실 rounding을 하기 전과는 완전히 다른 수라고 생각할 수 있으므로
rounding을 하고 난 평균을 rounding 하기 전 평균에 대신해서 사용하는 것이 타당하느냐 이거다.
그래서 stochastic rounding이라고 randomized rounding을 사용하는데 rounding하고 나서 기댓값이 하기 전 기댓값과
동일하도록 random하게 구성 요소 수치들을 올리거나 버리는 rounding을 한다고함.. 방법은 여러 가지가 있는 듯?
11. 또 다른 문제점?
머신러닝 모델은 점점 더 커지고 계산량이 복잡해지면서 32bit로 수치를 표현하여 사용하기에는 점점 한계가 다가오는 시대가 오고 있다.
그래서 low precision을 사용하여 machine learning을 시도하고 있는데 low precision은 32bit single precision에 비해 표현하는 수치는 적어지더라도 계산량이나 메모리 저장에서 적어도 절반은 줄어들 것이다.
그런데 32bit floating point를 16bit floating point로 바꿔서 training을 해보니 training loss가 떨어지다가 어느순간 커지는 현상이 발생했다고 한다.
왜 그런지 쉽게 생각하면 표현하는 수의 범위가 좁은 16bit로 바꾸면서 생기는 error에 의해 back propagation 과정에서 그 error가 누적되면서 loss가 떨어지지 않는다는 것이다.

12. mixed precision training
이 문제를 해결하기 위해 ‘mixed precision training, ICLR 2018’에서 새로운 training 방법을 제안했다.
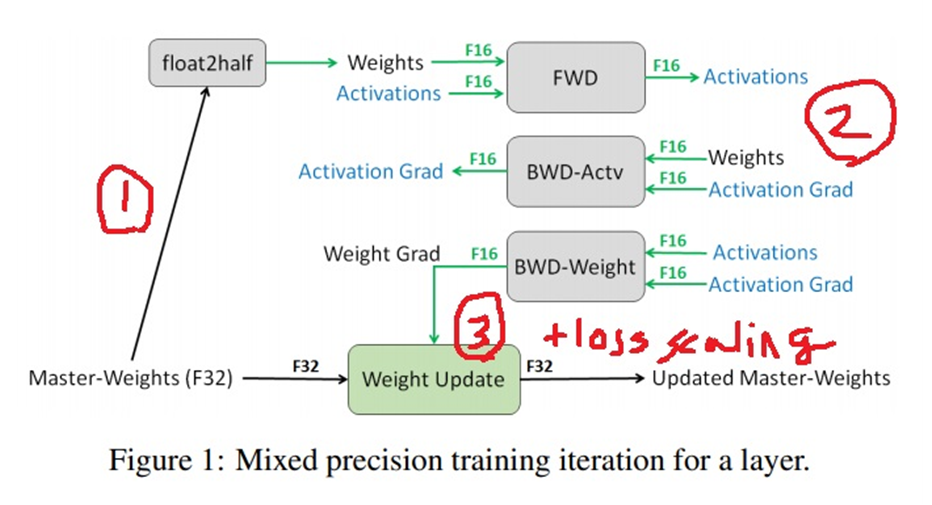
model의 weight(master weight라고 칭하나봄)를 16bit로 바꾼 뒤에 forward propagation과 backward propagation을 수행함
그리고 weight를 최종적으로 업데이트할때는 32bit로 변환하여 업데이트를 하는데 loss scaling이라는 기법을 사용함
잠깐 loss scaling이 무슨 말인데?
학습의 경우 weight, weight gradient, activation, activation gradient들이 거의 관여한다고 볼 수 있는데
논문의 저자들이 학습 과정을 관찰했을 때 대부분 weight, weight gradient는 16bit가 표현하는 수의 범위에 들어오는데
일부의 activation gradient가 16bit 범위를 넘어선다고 한다
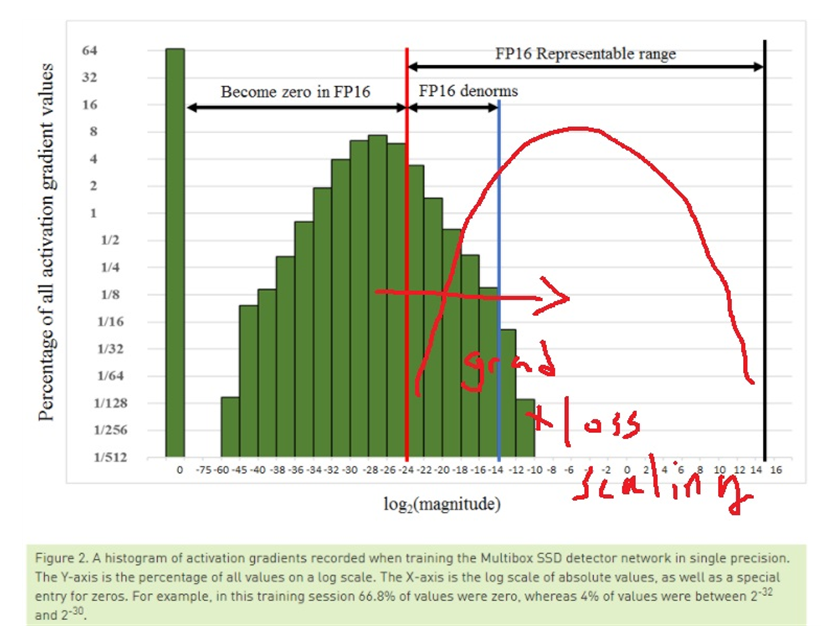
ssd object detector를 학습시킬 때 activation gradient가 초록색 히스토그램으로 나타나는데
히스토그램을 fp16 representable range로 옮기면 된다는 생각으로 gradient에 loss scaling factor를 곱하면 된다고 언급했다. (이 경우 8을 곱했다고 함)
추가적으로 논문을 더 읽어보면
weight 분포를 shift 하는 효과적인 방법중 하나로 One efficient way to shift the gradient values into FP16-representable range is to scale the loss valuecomputed in the forward pass, prior to starting back-propagation. 라고 언급하고 있다.
backward propagation을 하기 전에 forward pass에서 미리 옮기라고? 언급하고 있음
그래야 backward propagation이 간단해지고... gradient vanishing을 방지한다는 등 여러 가지 이유를 언급함
scaling factor를 선택하는 방법은 여러 가지가 있을 수 있지만 가장 단순한 방법으로 상수 scaling factor를 선택하라고 언급하고 있음
There are several options to choose the loss scaling factor. The simplest one is to pick a constant scaling factor. We trained a variety of networks with scaling factors ranging from 8 to 32K(many networks did not require a scaling factor).
8에서 32000?까지 실험해봤다고 했고 의외로 많은 경우는 심지어 scaling factor가 필요없다고도 말함

실험 결과로 성능이 조금 올랐다고 말함.. 속도라든지(당연히 속도는 빨라졌을 듯?) 그 외에 특별한 언급은 없음
13. mixed precision training 사용방법?
이론만 알아서는 필요가 없다고 느끼고 있다. 실제 어떻게 사용하는지 찾아봤는데
pytorch는 쉽게 사용하라고 이미 구현이 되어 있는 것 같음
굳이 하나하나 다 설명하는 것은 무리고 필요할 때 튜토리얼을 참고하여 사용
https://pytorch.org/docs/stable/notes/amp_examples.html
Automatic Mixed Precision examples — PyTorch 2.4 documentation
Shortcuts
pytorch.org
Introducing native PyTorch automatic mixed precision for faster training on NVIDIA GPUs
Most deep learning frameworks, including PyTorch, train with 32-bit floating point (FP32) arithmetic by default. However this is not essential to achieve full accuracy for many deep learning models. In 2017, NVIDIA researchers developed a methodology for m
pytorch.org
'딥러닝 > light weight modeling' 카테고리의 다른 글
| knowledge distillation 자세하게 (0) | 2024.09.24 |
|---|---|
| activation function quantization에 대하여 (0) | 2024.09.05 |
| Deep learning compiler란 무엇인가 (0) | 2024.08.29 |
| hardware-software codesign 개념 (0) | 2024.08.27 |
| AutoML의 개념 알아보기 (0) | 2024.08.23 |

