10진수를 다른 진법으로 바꾸는 방법

1. 1보다 큰 10진수를 다른 진수로 변환하는 방법

 

주어진 수를 변환하고자하는 진수의 base로 계속 나누고 나머지를 써둔다

 

마지막에 저장해둔 나머지 뒤에서부터 가지고옴

 

예를 들어 133은 3진법으로 변환하면 $11221_{(3)}$이다.

 

133을 3진법으로 변환하는 방법

 

 

2. 10진수 소수를 진수 바꾸는 방법

 

반면 소수는 방법이 조금 다른데 base를 계속 곱해나간 뒤 소수점을 넘은 정수는 옆에 따로 저장해두고

 

정수를 뺀 나머지를 다음 단계로 보낸 뒤 base를 계속 곱해

 

다음 단계로 보낸 나머지 부분이 0이 될때까지 반복함

 

정수 변환은 맨 뒤에서부터 앞으로 가지고 왔지만 맨 처음부터 따로 저장한 수를 맨 뒤까지 가지고 오면 끝

 

예를 들어 0.375는 8진수로 변환하면 $0.3_{(8)}$이고 0.1을 2진수로 변환하면 $0.00011....._{(3)}$으로 무한소수가 된다.

 

0.1을 2진수 변환하는 예시, 0.375를 8진수 변환하는 예시

 

 

0.1을 32bit floating point로 변환하여 저장한 예시

 

 

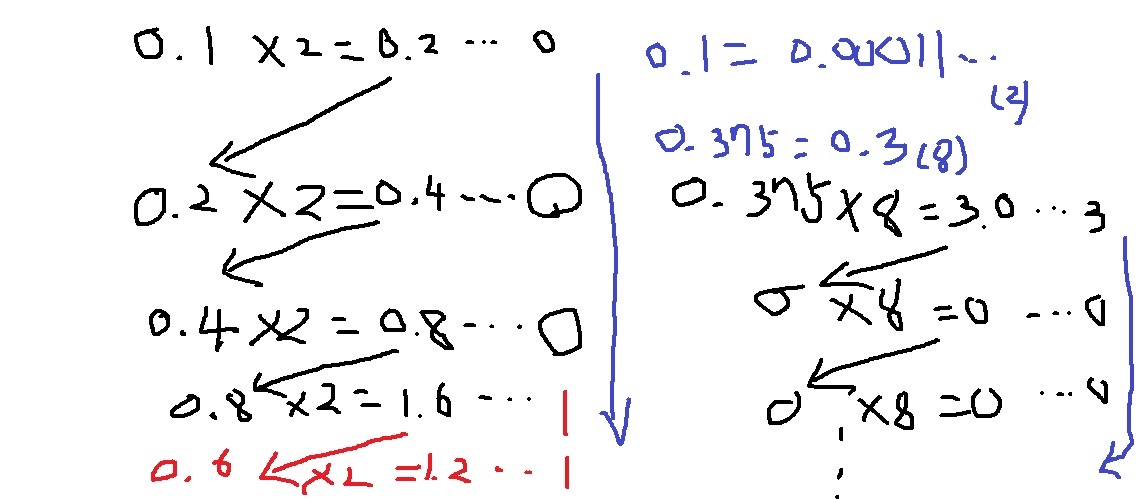
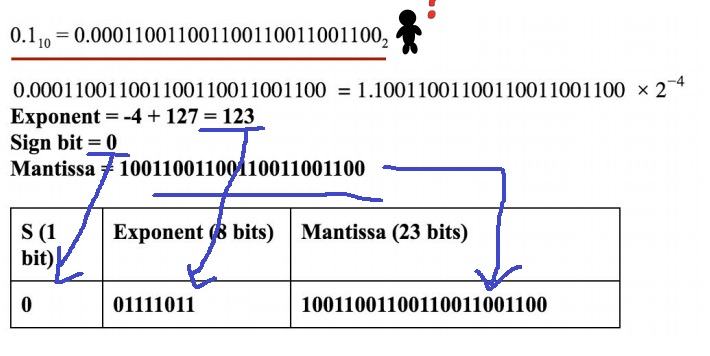
bias 변환한다는건 알았는데 그래도 -4를 바꿔서 저장하는줄 알았더니 -4+127=123을 바꿔서 저장하나봐

 

음수면 -를 비트로 또 저장해야하는데 그것을 방지하기위해 양수로 바꾸는 것