https://atcoder.jp/contests/abc349/tasks/abc349_d
D - Divide Interval
AtCoder is a programming contest site for anyone from beginners to experts. We hold weekly programming contests online.
atcoder.jp
L부터 R-1까지 연속된 정수 수열이 주어질때, 이 수열을 최소 개수의 구간으로 나눌려고 한다
L <= l1 < r1 = l2 < r2 = l3 < r3 ... < rm = R을 만족하는 (l1,r1), (l2,r2), ... , (lm,rm)에 대하여
$li = 2^{k}(j), ri = 2^{k}(j+1)$을 만족해야한다.
접근은 상당히 잘 했다
현재 시점 L을 기준으로 $L = 2^{k}j$를 만족하는 모든 k를 먼저 찾는다.
이거는 L이 2로 나누어 떨어지면, 2로 계속 나눠보면서 찾을 수 있는데 L의 최대는 $2^{60}$이니 충분하다.
그러면 각각의 k = k0, k1, k2, ...에 대하여..
$L = 2^{ki}ji$를 만족하는 ji를 찾을 수 있다.
그러면 다음 구간은 무조건 $X = 2^{ki}(ji+1)$이어야 한다.
최소 개수의 구간으로 분할해야하므로, X가 가장 큰 값을 그리디하게 잡아가면 된다.
당연히 [L,R]에서 분할해야하니 X는 R이하에서 잡아야한다.
import math
L,R = map(int,input().split())
s = L
division = []
while 1:
i = 0
p = s #현재 기준점 p에 대하여...
#p가 2로 나누어 떨어진다면...
#계속 나누면서 가장 큰 2의 지수를 구한다
while p % 2 == 0:
p //= 2
i += 1
p = s
max_j = 0
#다음 구간은 j = p//(2**k)이면 (j+1)(2**k)
#다음 구간의 시작점이 R이하여야한다.
#조건만 만족하면 그 값이 제일 큰 값이니 바로 break
for k in range(i,-1,-1):
j = p // (2**k)
if R >= (j+1)*(2**k):
max_j = j
break
if max_j != 0:
v = (max_j+1)*(2**k)
division.append((s,v))
s = v
else:
break
print(len(division))
for a,b in division:
print(a,b)
처음에 뭐 이런 느낌으로 코딩했는데
첫 시작점이 0인 경우 그러니까 [0,1024]에 대해서는 무한 반복되더라고
p = 0이면 0은 2로 나누어 떨어지는데 나눠도 0이니까 계속 나누어 떨어지거든
p = 0인 경우는 $0 = 2^{k}*0$이므로 k를 어떻게 잡더라도 $2^{k} = 2^{k}1$과 인접하게 된다.
따라서 R 이내에서 가장 큰 k를 찾으면 되는데 그거는 math.log2(R)이다.
R = 1024이면 math.log2(R) = 10이고 k = 10으로 하면 [0,1024]를 [0,1024]로 분할하면 된다
R = 1025라면 math.log2(1025) = 10.xxxx겠지.. 그래서 int(math.log2(1025)) = 10일 것이고..
[0,1024], [1024,1025] 2개의 구간으로 분할하면 된다
import math
L,R = map(int,input().split())
s = L
t = R
count = 0
division = []
while 1:
i = 0
p = s
if p == 0:
i = int(math.log2(R))
v = 2**i
division.append((s,v))
s = v
else:
while p % 2 == 0:
p //= 2
i += 1
p = s
max_j = 0
for k in range(i,-1,-1):
j = p // (2**k)
if R >= (j+1)*(2**k):
max_j = j
break
if max_j != 0:
v = (max_j+1)*(2**k)
division.append((s,v))
s = v
else:
break
print(len(division))
for a,b in division:
print(a,b)
그래서 이렇게 추가했는데 테스트 케이스 하나를 통과 못하더라?
원인을 계속 찾다보니....
math.log2()가 문제일까 생각했다
결과가 float니까 매우 큰 수에 대한 math.log2()는 오차가 있는게 아닐까 했는데 아니나 다를까 그게 맞다
2**60 = 1152921504606846976인데 이것보다 1 작은 값이나 1976작은 값이나 모두 60.0으로 내놓더라고
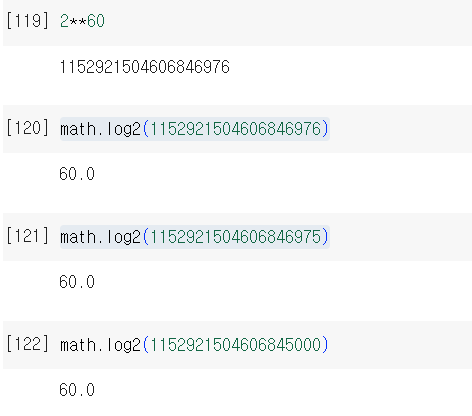
이런 테스트케이스에 걸려서 에러난듯
그래서 math.log2()를 쓰지 말고 단순히 정수 연산으로 p = 0인 경우 R이내의 가장 큰 2의 거듭제곱을 찾는다
value = 1
i = 0
while value*2 <= R:
i += 1
value *= 2
초기값 value = 1로 두고, 지수 i = 0으로 둔 다음...
value *2 <= R이면 value에 2를 곱해주고 지수 i 에 1을 증가시킨다..
어느 순간 value에 2를 곱했더니 R보다 커지면, 현재 i가 R 이내에서 가장 큰 2의 거듭제곱값이다.
그러니까 오차없이 정확한 int(math.log2(R))이 된다.
import math
L,R = map(int,input().split())
s = L
division = []
while s < R:
i = 0
p = s
if p == 0:
value = 1
while value*2 <= R:
i += 1
value *= 2
else:
while p % 2 == 0:
p //= 2
i += 1
p = s
max_j = -1
for k in range(i,-1,-1):
j = p // (2**k)
if R >= (j+1)*(2**k):
max_j = j
break
if max_j != -1:
v = (max_j+1)*(2**k)
division.append((s,v))
s = v
else:
break
print(len(division))
for a,b in division:
print(a,b)
조금 더 깔끔하게 짤려면
L,R = map(int,input().split())
division = []
while L < R:
i = 0
#i = 0부터 시작해서 L이 2^(i+1)로 나누어 떨어지면서..
#다음 점 (L//(2^(i+1)+1)*(2^(i+1))이 R 이하라면...
#i를 1 증가시킨다..
#이렇게 R 이내에서 조건을 만족하는 가장 먼 점을 찾는다
while L % (2**(i+1)) == 0 and (L//(2**(i+1))+1)*(2**(i+1)) <= R:
i += 1
#반복문이 끝나면 해당 i를 찾았고, 구간을 갱신
j = L//(2**i)
max_j = (j+1)*(2**i)
division.append((L,max_j))
L = max_j
print(len(division))
for a,b in division:
print(a,b)
근데 참 신기한게 마지막에 L = R이 반드시 된다는게 신기한것 같기도하고
'프로그래밍 > Python' 카테고리의 다른 글
| 딥러닝 중 UnidentifiedImageError: cannot identify image file 의 에러가 나올때 (0) | 2024.04.22 |
|---|---|
| colab에서 데이터를 준비하는 필수 명령어 wget, gunzip, unzip, tar xf, (0) | 2024.04.22 |
| functools.partial을 이용하여 기존 함수를 재활용한 새로운 함수 만들기 (0) | 2024.04.13 |
| 머신러닝에서 hyperparameter search를 도와주는 optuna 라이브러리 소개 (0) | 2024.04.02 |
| -1 의 50만 거듭제곱을 -1**(500000)으로 하면 안되는 이유 (0) | 2024.02.17 |

