1. 그래프와 트리
그래프(graph)란 정점들과 정점 둘을 잇는 간선들로 이루어진 집합

위는 9개의 정점(원)과 10개의 간선(실선)들로 이루어진 그래프이다.
각 원의 내부에 쓰여 있는 숫자는 편의상 정점에 매긴 번호를 의미한다.
간선(edge)은 항상 두 정점을 잇게 된다.
그래프의 간선에는 가중치가 있을 수 있다. 특별한 언급이 없다면 간선의 가중치는 1로 간주할 수 있다.
가중치가 존재한다면, 예를 들어 1-3 간선의 가중치가 3이라면 1번 정점에서 3번 정점으로 가기 위해선 길이 3인 간선을 지나야한다고 표현한다.
그래프의 간선에는 방향성이 있을 수 있다.
예를 들어 1번 정점과 3번 정점사이 놓인 1-3 간선의 경우 1 > 3 또는 3 > 1 방향성을 가지는 것이 가능하다.
방향성 간선을 갖고 있는 그래프는 유향 그래프(directed graph), 방향성이 없는 간선만으로 이루어진 그래프를 무향 그래프(undirected graph)라고 한다.
간선의 방향성은 그래프에서 탐색을 진행할 때 결과를 달리할 수 있다.
예를 들어 현재 위의 그래프에서 1번 정점에서 4번 정점까지 가면서 간선을 최소한 거치는 경로는 1 > 3 > 4로 2개의 간선을 거친다.
우리는 이것을 '1번 정점과 4번 정점의 최단 경로는 2다'라고 표현한다.
하지만 만약 3번 정점과 4번 정점 사이 간선이 4 > 3의 방향성을 가진다면.?
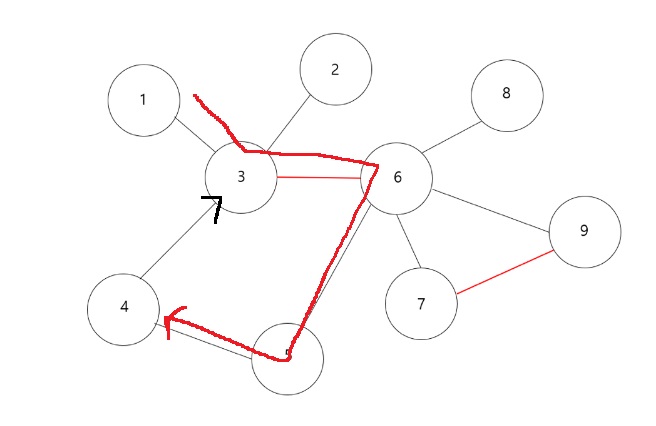
3번에서 4번으로 갈 수 없으므로 1 > 3 > 6 > 5 > 4로 돌아가야한다.
총 4개의 간선을 지나므로 최단 경로는 4가 된다.
그래프에서는 사이클을 정의할 수 있다.
무향 그래프에서 사이클이란, 어떤 정점에서 출발해 시작점을 제외한 어떤 정점도 어떤 간선도 두 번 이상 방문하지 않고 시작점으로 돌아올 수 있는 경로를 의미한다.

예를 들어 위 그래프에서는 3 - 6 - 5 - 4 - 3 사이클과 6 - 7 - 9 사이클이 존재한다.
1 - 3 - 1은 1-3 간선을 두번 지나서 사이클이 아니고, 1 - 3 - 6 - 5 - 4 - 3은 시작점 1로 돌아오지 않으므로 사이클이 아니다.
만일 그래프에서 단 하나의 사이클도 없다면 해당 그래프는 '트리(tree)'라고 부른다.
이는 그래프가 마치 하나의 정점에서 출발해 피어난 나무 모양과도 같음에 붙여진 이름으로 예를 들어 위 그림에서 빨간 간선 2개를 제거하면 트리가 된다.
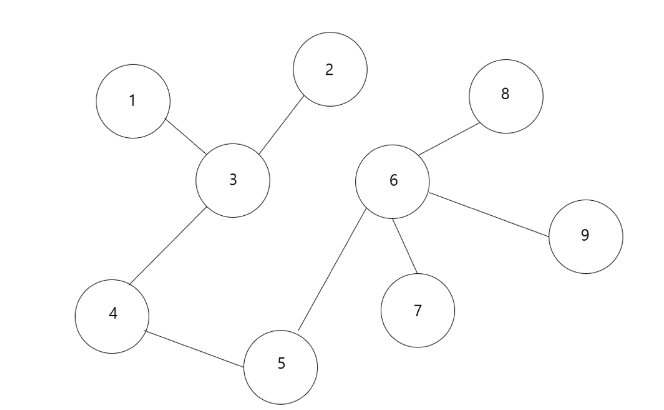
일반적으로 그래프에서는 정점의 위치나 간선의 모양 등에 대한 조건은 전혀 고려하지 않고, 오직 연결성만을 고려한다.
간선의 집합이 변하지 않는다는 가정 하에 그래프를 얼마든지 다시 그릴 수가 있다.
5번 정점을 잡고 위로 들어올린다면...
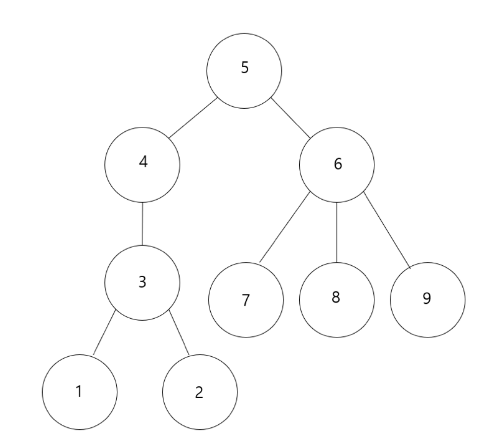
트리에는 루트(root)가 있을 수도 없을 수도 있지만, 편의를 위해서라면 아무 정점이나 루트로 선택할 수 있다.
5번 정점을 편의상 루트로 생각하고 트리를 다시 본다면...
트리는 항상 루트를 기준으로 다시 그릴 수 있기 때문에, 루트가 고정되지 않는 한 어떤 정점이 '위에' 있는지 판정할 수 없다.
하지만 루트가 고정된다면, 우리는 정점 간에 '부모'와 '자식'의 관계를 정의할 수 있다.
위 트리에서는 4번 정점의 부모는 5번 정점이고 3번 정점은 4번 정점의 자식이다.
5번 정점의 부모는 없으며 4,6번 정점을 두 자식으로 갖게 된다.
트리에는 몇가지 중요한 성질이 있는데 증명 없이 받아들이자.
1) 트리는 사이클이 없는 무향 그래프이다.
2) 루트를 제외한 모든 정점의 부모는 오직 1개이다.
3) 정점이 n개이면 간선은 n-1개 있다.
4) 임의의 두 정점 u와 v에 대하여 u에서 v로 가는 경로는 유일하다.
5) 임의의 두 정점 u,v 는 서로 도달 가능하다.
6) 아무 정점이나 잡고 부모와의 연결을 끊으면, 해당 정점과 그 정점의 모든 자식들로 이루어진 부분그래프는 트리이다.
6)으로 만들어진 부분그래프를 '서브트리'라고 부른다.
2. 트리를 만드는 방법
입력이 루트와 자식들로 이루어진다면 좋겠지만 정점의 개수와 간선의 목록만이 주어진다면 어떻게 부모 - 자식의 트리 형태로 바꿀 수 있을까?
예를 들어 위 트리가 다음과 같은 입력으로 주어진다면...
9
1 3
4 3
5 4
5 6
6 7
2 3
9 6
6 8
보통 트리라고 주어지고 정점의 개수가 n개가 주어진다면.. 간선의 개수는 말하지 않아도 n-1개이다.
물론 말해주는 경우도 많다.
위와 같은 데이터를 트리로 구성하고 싶다면 임의로 루트를 잡는게 편하다.
만약 5번을 루트라고 지정한다면...
현재 노드 current의 연결된 node를 모두 순회하여... node가 current의 부모 노드가 아니라면, 그 node는 current의 자식이다.
def make_tree(current,parent): #현재 노드, 해당 노드의 부모 노드
for node in edges[current]: #현재 노드와 연결된 노드들을 순회하여..
if node != parent: #연결된 노드가 현재 노드의 부모가 아니라면...
tree[current].append(node) #그 노드는 현재 노드의 자식 노드이다.
make_tree(node,current)
n = int(input())
tree = [[] for _ in range(n+1)]
edges = [[] for _ in range(n+1)]
for _ in range(n-1):
u,v = map(int,input().split())
edges[u].append(v)
edges[v].append(u)
make_tree(5,-1) #루트는 5번이고 루트의 부모는 없다(-1)
print(tree)
9
1 3
4 3
5 4
5 6
6 7
2 3
9 6
6 8
[[], [], [], [1, 2], [3], [4, 6], [7, 9, 8], [], [], []]
5번이 4,6을 자식으로 가지고 4번이 3을 자식으로 가지고 3번이 1,2를 자식으로 가지고 6번이 7,8,9를 자식으로 가진다.
3. 연습문제
15681번: 트리와 쿼리
트리의 정점의 수 N과 루트의 번호 R, 쿼리의 수 Q가 주어진다. (2 ≤ N ≤ 105, 1 ≤ R ≤ N, 1 ≤ Q ≤ 105) 이어 N-1줄에 걸쳐, U V의 형태로 트리에 속한 간선의 정보가 주어진다. (1 ≤ U, V ≤ N, U ≠ V)
www.acmicpc.net
이제 임의의 루트가 있는 트리가 주어지고 다음과 같은 질의가 여러개 주어진다면.. 어떻게 해결할 수 있을까?
'정점 U를 루트로 하는 서브트리가 포함하는 정점의 수는 몇개인가?'
정점 U를 루트로 하는 서브트리는 U와 부모의 연결을 끊고 U를 기준으로 모든 자식들을 포함하는 트리를 말한다.
예를 들어 다음 트리에서 6번을 루트로 하는 서브트리는 정점 4개를 가지고 있다.
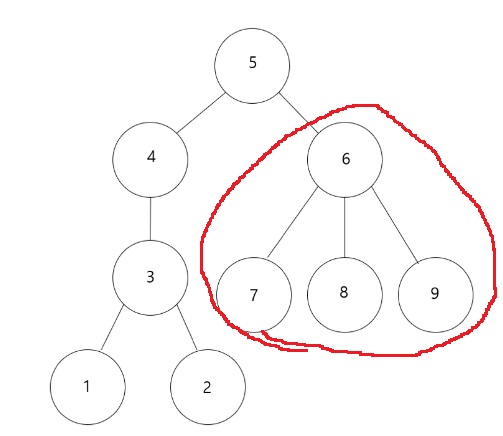
물론 리프노드인 8번 정점을 루트로 하는 서브트리의 정점의 수는 8번 정점 1개이다.
쉽게 생각할 수 있는 방법은 질의가 주어질때마다 연결을 끊어서 해당 서브트리에서 정점의 수를 세어볼 수 있겠지만,
정점의 수가 매우 많고 질의도 매우 많으면 시간내에 수행하지 못할 가능성이 높다.
따라서 미리 모든 정점에 대해 해당 정점을 루트로 하는 서브트리의 정점의 수를 구해놓는 방법이 있다면 좋을 것이다.
def treedp(current):
for child in tree[current]: #현재 정점의 자식을 순회하여,
treedp(child)
dp[current] += dp[child] #자식이 가지고 있는 정점의 수를 모두 더해준다
루트부터 시작해서, 현재 정점의 자식을 방문하여 현재 정점의 자식 정점이 가지고 있는 정점의 수를 다이나믹 프로그래밍 형태로 부모 정점에 더해주면 된다
from sys import stdin,setrecursionlimit
setrecursionlimit(10**6)
def make_tree(current,parent): #현재 노드, 해당 노드의 부모 노드
for node in edges[current]: #현재 노드와 연결된 노드들을 순회하여..
if node != parent: #연결된 노드가 현재 노드의 부모가 아니라면...
tree[current].append(node) #그 노드는 현재 노드의 자식 노드이다.
make_tree(node,current)
def treedp(current):
for child in tree[current]: #현재 정점의 자식을 순회하여,
treedp(child)
dp[current] += dp[child] #자식이 가지고 있는 정점의 수를 모두 더해준다
n,r,q = map(int,stdin.readline().split())
tree = [[] for _ in range(n+1)]
edges = [[] for _ in range(n+1)]
dp = [1]*(n+1) #모든 정점 U를 루트로 하는 서브트리는 U를 일단 1개 포함하고 있다
for _ in range(n-1):
u,v = map(int,stdin.readline().split())
edges[u].append(v)
edges[v].append(u)
make_tree(r,-1) #루트는 r번이고 루트의 부모는 없다(-1)
treedp(r)
for _ in range(q):
u = int(stdin.readline())
print(dp[u])
4. 트리를 구성하지 않고 해결하는 방법
위 코드를 보면 트리에서의 다이나믹 프로그래밍은 리프노드까지 탐색하여 올라오면서 부모 정점에 값을 더해나가는 방식이다
트리에서의 다이나믹 프로그래밍이라고 해서, 트리를 반드시 직접 구현할 필요는 없다
일반적인 재귀 DFS에서 한번 방문한 곳의 visited를 복구해주는 형태로
def dfs(u):
for v in tree[u]:
if visited[v] == 0:
visited[v] = 1
dfs(v)
visited[v] = 0
구현하는데... 일반적인 그래프에서 visited를 복구해주지 않는다면 트리를 탐색하는 것과 동일한 효과를 얻는다
def dfs(u):
for v in tree[u]:
if visited[v] == 0:
visited[v] = 1
dfs(v)
주어진 입력에서 트리를 구성하지 않고 DFS만으로 다음과 같이 해결할 수 있다
정점 u의 연결된 노드들을 탐색해나가는데, 방문하지 않았다면 방문하고...
DFS가 끝났다면 부모 정점의 정점 수 DP[u]에 현재 자식 v의 정점 수 DP[v]를 더해나간다
방문이 끝나고 나서 visited[v] = 0으로 하지 않는다
from sys import stdin,setrecursionlimit
setrecursionlimit(1000000)
def dfs(u):
for v in tree[u]:
if visited[v] == 0:
visited[v] = 1
dfs(v)
#DFS가 끝났다면 부모 정점의 정점 수 DP[u]에 현재 자식 v의 정점 수 DP[v]를 더해나간다
#방문이 끝나고 나서 visited[v] = 0으로 하지 않는다
dp[u] += dp[v]
n,r,q = map(int,stdin.readline().split())
tree = [[] for _ in range(n+1)]
#dp[u]는 u를 루트로 하는 서브트리에서 포함하는 정점의 수
#모든 서브트리는 루트 1개를 반드시 포함하니 1부터 시작
dp = [1]*(n+1)
visited = [0]*(n+1)
for _ in range(n-1):
u,v = map(int,stdin.readline().split())
tree[u].append(v)
tree[v].append(u)
visited[r] = 1 #루트부터 탐색 시작
dfs(r)
for _ in range(q):
u = int(stdin.readline())
print(dp[u])
https://chanhuiseok.github.io/posts/algo-56/
알고리즘 - 트리 DP 문제 풀기(트리에서의 Dynamic Programming)
컴퓨터/IT/알고리즘 정리 블로그
chanhuiseok.github.io
'알고리즘 > 다이나믹 프로그래밍' 카테고리의 다른 글
| job assignment problem으로 알아보는 비트마스킹을 이용한 다이나믹 프로그래밍 (0) | 2024.03.27 |
|---|---|
| 방향 비순환 그래프(DAG)위에서 다이나믹 프로그래밍 배우기 (0) | 2024.01.08 |
| 다이나믹 프로그래밍 테크닉 - 어떤 것을 선택하거나 선택하지 않아서 부분집합을 만드는 방법의 수 (0) | 2023.11.15 |
| 문자열 3개의 가장 긴 공통 부분문자열(Longest Common Subsequence)구하기 (0) | 2023.10.28 |
| LCS(Longest Common Subsequence) 문제 다이나믹 프로그래밍 기본 해법 배우기 (0) | 2023.10.28 |

