1. 문제
11660번: 구간 합 구하기 5 (acmicpc.net)
11660번: 구간 합 구하기 5
첫째 줄에 표의 크기 N과 합을 구해야 하는 횟수 M이 주어진다. (1 ≤ N ≤ 1024, 1 ≤ M ≤ 100,000) 둘째 줄부터 N개의 줄에는 표에 채워져 있는 수가 1행부터 차례대로 주어진다. 다음 M개의 줄에는 네
www.acmicpc.net
2. 풀이
좌상단이 (0,0)이고 우하단이 (x,y)인 직사각형내의 모든 원소 합을 dp[y][x]라고 정의한다.
예를 들어 다음 그림을 보면... dp[3][4]는??

dp[3][4] = 1+2+3+4+2+3+4+5+3+4+5+6을 뜻하게 된다.
어떻게 하면 이전에 구해놓은 합을 이용해서 쉽게 구할 수 있을까?
다음과 같이 x = 0 ~ n, y = 0 ~ m 차례대로 순회하면서 x = 4이고 y = 3이 될때,
이전에 x = 3, y = 3인 부분(파란색), x = 4, y = 2인 부분(초록색)이 이미 구해져있다.
초록색 부분과 파란색 부분의 합에 (4,3)의 원소인 6을 더해주면 되는데..

dp[3][4] = dp[3][3] + dp[2][4] + A[3][4]로만 한다면... 위 그림에서 볼 수 있듯이 겹치는 부분이 2번 더해진다
그래서 겹치는 부분도 빼줘야한다
일반적으로 생각해보면... (x,y)까지의 합인 dp[y][x]는...
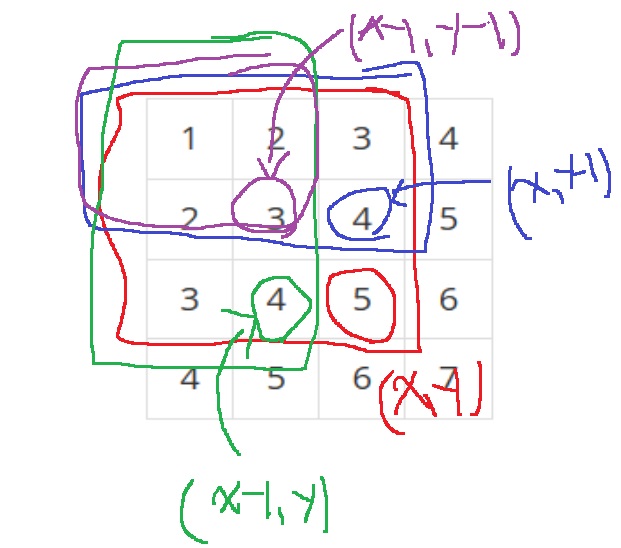
(빨간색 부분) = (파란색 부분) + (초록색 부분) + (x,y)원소 - (보라색 부분)
dp[y][x] = dp[y-1][x] + dp[y][x-1] + A[y][x] - dp[y-1][x-1]
그런데 이렇게 한다면 사실 문제가 되는 부분은 x = 0, y = 0인 부분인데
예를 들어 y = 0인 경우를 생각해보면..?
다음과 같이 초록색 부분밖에 안남아서.. dp[y][x] = dp[y][x-1] + A[y][x]

즉 인덱스가 -1이 되는 부분은 0으로 없어진다
x = 0인 경우를 생각해봐도.. 초록색 부분이 없어지고 파란색 부분만 남는다
dp[y][x] = dp[y-1][x] + A[y][x]

구현방법에 따라 다르긴 하겠지만...
기본적으로 dp[y][x] = dp[y-1][x] + dp[y][x-1] + A[y][x] - dp[y-1][x-1]로 dp배열을 채워넣고,
인덱스가 음수가 되는 부분은 0으로 처리해주고
from sys import stdin
n,m = map(int,stdin.readline().split())
matrix = [list(map(int,stdin.readline().split())) for _ in range(n)]
#dp[y][x] = 좌상단 (0,0) 우하단 (x,y)까지 사각형의 모든 원소의 합
dp = [[0]*(n+1) for _ in range(n+1)]
dp[0][0] = matrix[0][0]
for y in range(1,n):
dp[y][0] = matrix[y][0] + dp[y-1][0]
for x in range(1,n):
dp[0][x] = matrix[0][x] + dp[0][x-1]
for y in range(1,n):
for x in range(1,n):
dp[y][x] = dp[y-1][x] + dp[y][x-1] + matrix[y][x] - dp[y-1][x-1]
그렇지만 dp배열은 (0,0)에서 (x,y)까지의 합만을 알려주는데...
진짜 알고 싶은 부분은 좌상단이 (x1,y1)이고 우하단이 (x2,y2)인 직사각형 내의 모든 원소의 합을 알고 싶을 때가 있다
어떻게 알 수 있을까
(0,0)에서 (x,y)까지의 합만 알고 있다는 사실을 이용해서 위와 똑같이 생각하면 된다

파란색 부분인 (x1,y1) ~ (x2,y2)의 합은...
(0,0)~(x2,y2)까지의 합(빨간색 부분)에서 (0,0)~(x2,y1-1)까지의 합(초록색 부분)과 (0,0)~(x1-1,y2)까지의 합(보라색 부분)을 빼주고
이러면 겹치는 부분인 (0,0)~(x1-1,y1-1)까지의 합(주황색 부분)은 두번 빼지므로 더해주면 된다
(구하고자 하는 합) = dp[y2][x2] - dp[y1-1][x2] - dp[y2][x1-1] + dp[y1-1][x1-1]
인덱스가 음수가 되는 경우인 x1 = 0이나 y1 = 0인 경우, 0으로 처리해주면 될 것이다.
식을 외울 필요는 없고, 그냥 위 그림을 그려보면 바로 식을 도출할 수 있다
#2차원 배열 누적합
#유도된 식은 그림을 그려보면 바로 도출할 수 있다
from sys import stdin
n,m = map(int,stdin.readline().split())
matrix = [list(map(int,stdin.readline().split())) for _ in range(n)]
#dp[y][x] = 좌상단 (0,0) 우하단 (x,y)까지 사각형의 모든 원소의 합
dp = [[0]*(n+1) for _ in range(n+1)]
#dp[y][x] = dp[y-1][x] + dp[y][x-1] + matrix[y][x] - dp[y-1][x-1]
#x = 0이거나 y = 0인 경우 해당 dp값은 0으로 처리
dp[0][0] = matrix[0][0]
for y in range(1,n):
dp[y][0] = matrix[y][0] + dp[y-1][0]
for x in range(1,n):
dp[0][x] = matrix[0][x] + dp[0][x-1]
for y in range(1,n):
for x in range(1,n):
dp[y][x] = dp[y-1][x] + dp[y][x-1] + matrix[y][x] - dp[y-1][x-1]
#(x1,y1)~(x2,y2)까지의 합은..
#dp[y2][x2] - dp[y1-1][x2] - dp[y2][x1-1] + dp[y1-1][x1-1]
#역시 x1 = 0 이거나 y1 = 0인 경우 해당 dp는 0으로 처리
for _ in range(m):
y1,x1,y2,x2 = map(int,stdin.readline().split())
x1 -= 1
y1 -= 1
x2 -= 1
y2 -= 1
A = dp[y2][x2]
if y1 == 0:
B = 0
else:
B = dp[y1-1][x2]
if x1 == 0:
C = 0
else:
C = dp[y2][x1-1]
if x1 == 0 and y1 == 0:
D = 0
else:
D = dp[y1-1][x1-1]
print(A - B - C + D)'알고리즘 > 누적 합 알고리즘' 카테고리의 다른 글
| 누적합 응용 - prefix/suffix min/max 배열 이용한 테크닉 (0) | 2024.02.12 |
|---|---|
| 거짓말하는 사람 수 알아내는 방법(놀라운 양방향 누적합 테크닉) (0) | 2024.02.05 |
| 정수 M으로 나누어 떨어지는 부분 구간합을 선형시간에 구하는 놀라운 방법 (0) | 2023.06.06 |
| 수열의 구간 합을 빠르게 계산하는 방법1 -접두사 합(prefix sum)- (0) | 2022.10.30 |
| 이차원 배열끼리 덧셈은 어떻게 효율적으로 할 수 있을까 (0) | 2022.04.19 |

