1. z - function
길이 n인 문자열 s에 대하여 z[i]는 s의 i번째 접미사 s[i,i+1,...]과 s와의 최대 공통 접두사의 길이를 말한다
정의에 의하면 z[0]는 s와 s의 최대 공통 접두사의 길이로 s 그 자체의 길이 n이 될텐데 일반적으로 잘 정의하지 않는다.
z[0] = 0으로 정의하기도 하고 문제에 따라 필요하다면 z[0] = n으로 정의하기도 한다.
예를 들어 'abacaba'에 대하여...
z[1]은 'abacaba'와 'bacaba'의 최대 공통 접두사의 길이로... 공통 접두사가 존재하지 않으니 0
z[2]는 'abacaba'와 'acaba'의 최대 공통 접두사의 길이로 'a'가 있으니 z[2] = 1
z[3]은 'abacaba'와 'caba'의 최대 공통 접두사의 길이로 공통 접두사가 존재하지 않으니 0
z[4]는 'abacaba'와 'aba'의 최대 공통 접두사의 길이로 'aba'가 최대 공통 접두사가 되니까 3이다.
z[5]는 'abacaba'와 'ba'의 최대 공통 접두사의 길이로 공통 접두사가 존재하지 않으니 0
z[6]은 'abacaba'와 'a'의 최대 공통 접두사의 길이로 'a'가 최대 공통 접두사가 되니까 1이다.
2. $O(n^{2})$
단순하게는 $O(n^{2})$에 다음과 같이 구현 가능하다.
def z_function(s):
n = len(s)
z = [0]*(n)
for i in range(1,n):
#z[i]는 s의 시작 인덱스
#i+z[i]는 i번째 접미사 s[i,i+1,...]의 시작 인덱스
#서로 같으면 z[i]를 1 증가시켜 다음 문자를 비교
#서로 다르면 거기서 끝
while i + z[i] < n and s[z[i]] == s[i+z[i]]:
z[i] += 1
return z
print(z_function('abacaba'))
[0, 0, 1, 0, 3, 0, 1]
코드만 보면 뭔소린가 그렇긴 한디
z[i]가 0부터 시작하니 z[i]는 s의 인덱스, i+z[i]는 i번째 접미사 s[i,i+1,...]의 인덱스이고 서로 같으면 z[i]를 1 증가시켜가며 비교
예를 들어 z[2]를 구하고 싶다면 다음과 같이 s[0]과 s[2]를 비교해서

서로 같으니 z[2] += 1이 될거고, 다음 z[2] = 1인 상태에서는 서로 문자가 다르니 z[2] = 1로 끝이다.

결국 i+z[i]는 s 문자열 내에서만 움직일 수 있으니 i+z[i] < n일때만 가능하다.
3. efficient algorithm
z[i]는 최대 공통 접두사의 길이를 나타내므로 이전에 계산된 값들을 활용해서 효율적인 구현이 가능하다.
z[i]는 i에서 시작해서 i+z[i]-1로 끝나는, s의 접두사와 동일한 부분문자열의 길이와 같아야한다.

여기서 [left,right)를 현재까지 s의 접두사와 일치한 모든 부분문자열 중에서 끝점이 가장 오른쪽에 있는 부분문자열이라고 하자.

여기서 i가 right보다 크거나 같다면..?
위에서 단순하게 z[i]를 1씩 증가시키는 방법으로 새롭게 일치되는 최대 공통 접두사를 찾아야한다.
while i+z[i] < n and s[z[i]] == s[i+z[i]]:
z[i] += 1
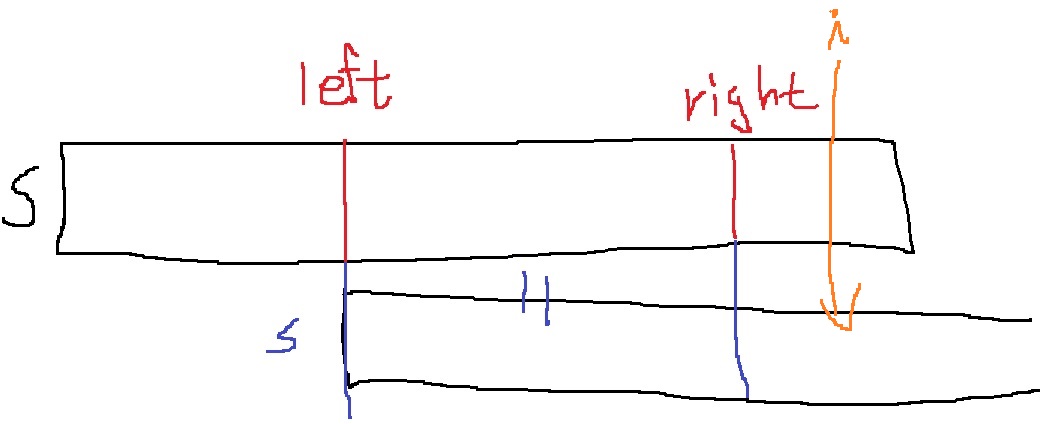
이 때 새롭게 일치되는 부분문자열을 찾을 수 있는데,
[left,right)를 가장 오른쪽에 있는 s의 접두사와 일치하는 부분문자열로 정의했으므로,
왼쪽 점은 i이고 오른쪽 점은 i + z[i]일테니까, i+z[i] 가 right보다 크다면, 새롭게 left,right를 갱신해준다
i는 안움직이고 z[i]만 1씩 증가하니까, i가 왼쪽점 i+z[i]가 오른쪽 점이다..

그런데 반대로 i < right일수 있다.
이 경우에는 z[i]값을 시작을 0으로 하지말고 이미 계산된 값을 이용해서 다른 지점에서부터 시작해볼 수 있지 않을까?

여기서 알 수 있는건, [left,right)가 s의 접두사와 일치하므로...
s의 접두사는 [left,right)를 왼쪽으로 left만큼 움직인 s[0,1,...right-left)와 일치한다는 뜻이다.

따라서 이 경우에는 z[i]는 이미 접두사가 동일하다고 확실한 z[i-left]부터 시작할 수 있다.
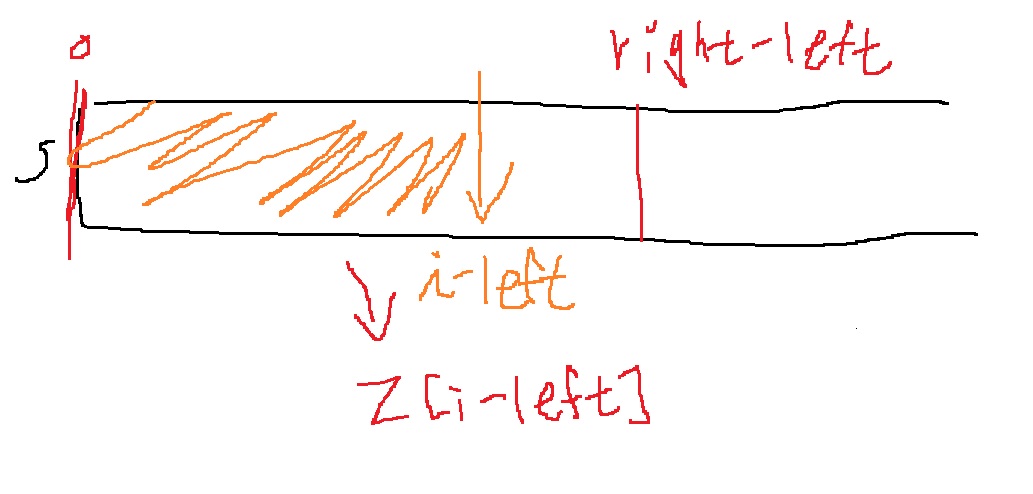
하지만 z[i-left]가 매우 클 수 있다. 위치 i에서 접미사와 s의 공통 접두사 길이를 구할건데,
i가 문자열의 마지막에 갈 수록 접미사의 길이는 짧아지는데, z[i-left]가 접미사 s[i:]보다 커진다면 문제가 된다.
예를 들어 문자열 s = aaaabaa라고 해보자.
마지막 위치인 i = 6에 도달했을때, [left,right) = [5,7) = "aa"가 된다.
이를 왼쪽으로 5만큼 옮기면 6-5 = 1이므로 z[6]을 구하기 위해 z[1]부터 시작할 수 있는데, z[1] = 3이다.(aaa가 최대 공통 접두사)
하지만 i = 6부터는.. 접미사의 최대 길이가 1이므로 최대 공통 접두사 길이가 3일 수 없다.
즉, i < right인 경우에 z[i]의 초기값은 z[i-left]와 right-i중 작은 값이 된다.
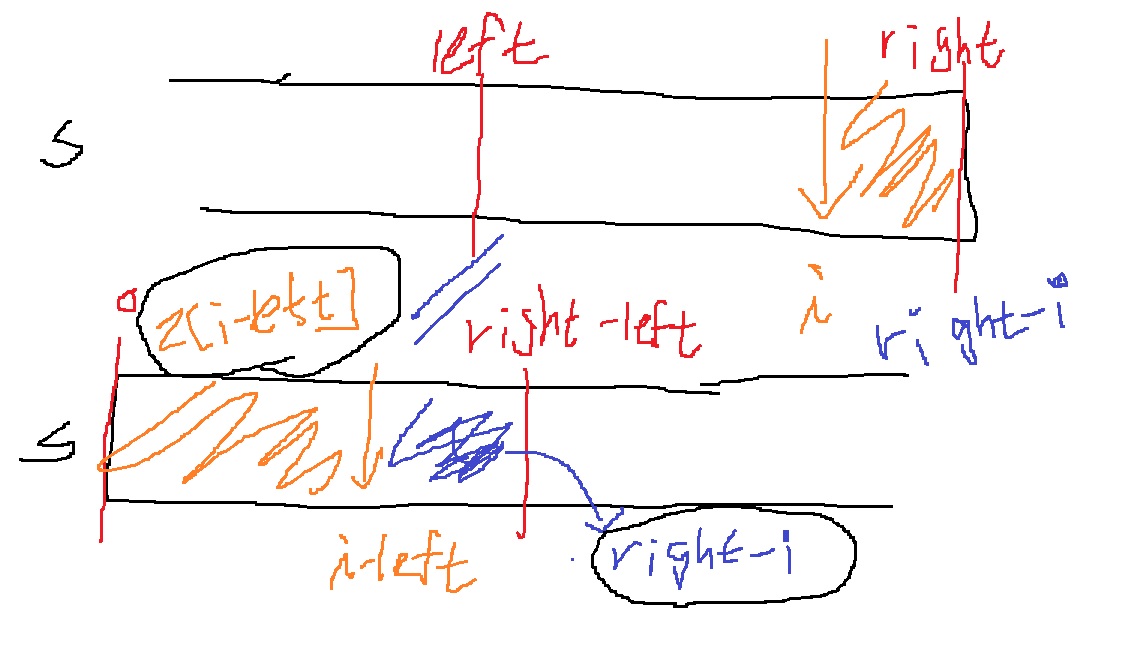
그러므로 정리하자면 다음과 같다.
1) left,right = 0, z = [0]*n으로 초기화
2) i = 1부터 n-1까지 순회하여...
2-1) i < right이면 z[i] = min(right - i, z[i-left])이다.
2-2) i >= right이면 z[i] = 0이다.
3) s[z[i]] == s[i+z[i]]이면 z[i]를 1 증가, i+z[i]가 문자열의 최대 인덱스 n-1을 넘지 않도록
4) 3)이 끝나면 left,right를 갱신한다.
새롭게 찾은 부분문자열은 왼쪽이 i이고 오른쪽이 i+z[i]이므로, i+z[i] > right이면,
left = i, right = i+z[i]로 갱신
#z algorithm
#문자열 s와 s의 i번째 접미사 s[i,i+1,...]의 가장 긴 공통 접두사의 길이 z[i]
def z_function(s):
n = len(s)
z = [0]*n
#z[0] = n #문제에 따라 필요하다면 정의
#지금까지 접두사와 일치한 구간 중 오른쪽 끝점이 가장 오른쪽에 있는 구간 [left,right]
left = 0
right = 0
for i in range(1,n):
if i < right: #현재 인덱스 i가 [left,right]안에 있다면....
#z[i]의 시작점은 0이 아니라 right-i, z[i-left]중 작은 것에서 시작할 수 있다.
z[i] = min(right - i, z[i - left])
#현재 인덱스 i가 [left,right]밖에 있다면 z[i]는 0에서 시작한다.
#z[i]부터 시작해서 s[z[i]]와 s[i+z[i]]가 같으면 z[i]를 1씩 증가
while i + z[i] < n and s[z[i]] == s[i+z[i]]:
z[i] += 1
#새로 일치하는 구간을 구했는데, 오른쪽 점 i+z[i]가 기존 right보다 크다면 새로 갱신
if i+z[i] > right:
left = i
right = i + z[i]
return z
print(z_function('abacaba'))
[0, 0, 1, 0, 3, 0, 1]
4. 연습문제
13713번: 문자열과 쿼리
첫째 줄에 문자열 S가 주어진다. (1 ≤ N ≤ 1,000,000) 둘째 줄에 쿼리의 개수 M이 주어진다. (1 ≤ M ≤ 100,000) 셋째 줄부터 M개의 줄에 각각의 쿼리 i가 주어진다. (1 ≤ i ≤ n)
www.acmicpc.net
5. 풀이
문자열 s와 s의 접두사 s[1,2,3,...,i]와의 가장 긴 공통 접미사의 길이를 구하는 문제
위의 z-function 구하는 과정을 반대로 생각하면서 구하면 답이 나오긴 한다
접미사의 길이를 구해야하므로, 인덱스 i는 n-1부터 0까지 움직인다.
하지만 i = n-1인 경우에는 s와 s의 가장 긴 공통 접미사의 길이를 구하므로, 그 자체가 된다.
즉 z[n-1] = n
그래서 i = n-2부터 0까지 움직여서.. 가장 긴 공통 접미사의 길이를 구한다.
s의 마지막 시작점은 인덱스로 -1인데 z 배열을 0으로 초기화한다면.. s[z[i]]는 의미 없게 된다.
-1부터 시작해서 -2,-3,-4,..로 움직여야하고 z[i]는 1씩 증가시킬 것이므로 s[-z[i]-1]과 s[i-z[i]]를 비교하면 된다.
또한 i - z[i]는 0까지 움직일 수 있다.
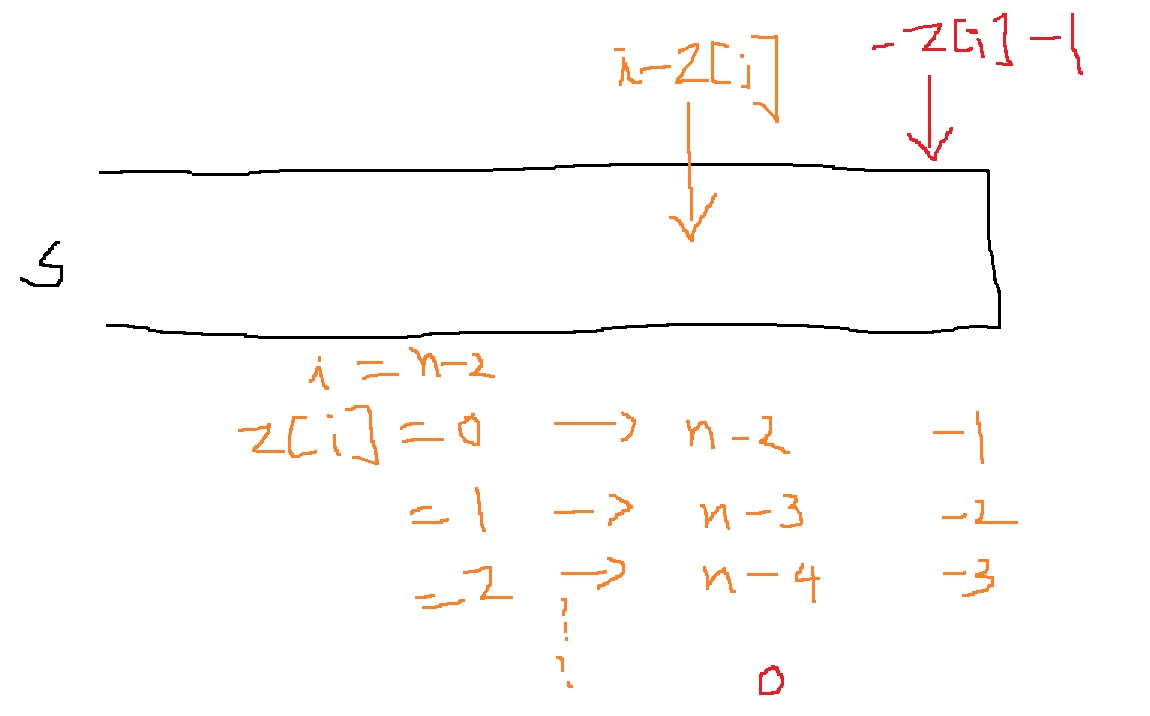
def z_function(s):
n = len(s)
z = [0]*n
z[n-1] = n
for i in range(n-2,-1,-1):
while i-z[i] >= 0 and s[-z[i]-1] == s[i-z[i]]:
z[i] += 1
근데 길이가 100만이나 될 수 있으니 이렇게 구하면 당연히 시간 초과일거고... 위에서 배운 테크닉을 역으로 적용해보면
지금까지 구한 접미사가 일치하는 부분 문자열중 왼쪽 점이 가장 왼쪽에 있는 구간을 [left,right]라고 해서..
현재 인덱스 i가 이 구간 밖에 있는가? 즉 i < left인가?
이 구간 안에 있는가? i > left인가?

i < left이면 일치하는 부분이 없으니 기존 방법대로 z[i]는 0부터 시작하도록 하고
i > left이면 일치하는 부분을 찾기 위해 right를 n-1로 옮겨서..
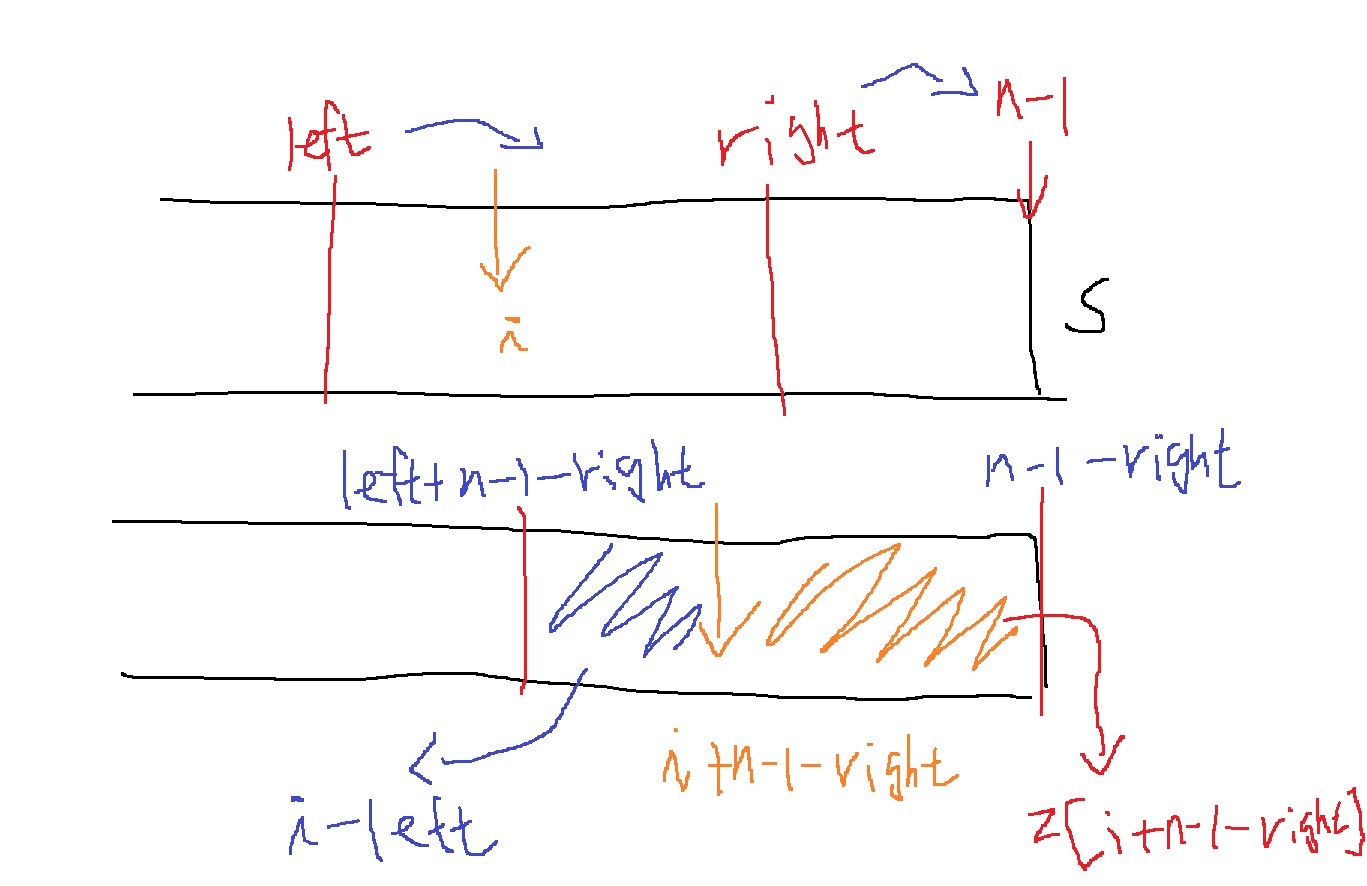
이제 i > left인 경우에는 z[i+n-1-right]가 확실하게 일치하므로 이를 z[i]의 시작점으로 삼을 수 있다.
하지만 위에서 본 것처럼 이 또한 i = 0에 가까울수록 접두사 s[1,2,..,i]는 짧아지나,
z[i+n-1-right]가 이보다 길어질 수 있으므로... i-left를 대안으로 삼아야한다.
따라서 i > left인 경우에는 z[i]는 z[i+n-1-right]와 i-left중 작은 값으로 시작한다.
그리고 항상 왼쪽 끝점이 최대한 왼쪽으로 가도록 갱신시켜줘야하므로, z[i]가 1씩 증가하면서
왼쪽 점은 i-z[i]이고 오른쪽 점은 i이니까... 새로 구한 구간이 i-z[i] < left로 왼쪽으로 멀어진다면 left,right를 갱신해준다.
당연하지만 n-1부터 시작하니 left,right의 초기값은 n-1이다.
#z_function을 구하는 방법을 이용한
#s와 접두사 s[1,2,..,i]의 가장 긴 공통 접미사의 길이 z[i]를 구하는 함수
#기존 z_function 구하는 과정을 반대로 생각
def z_function(s):
n = len(s)
z = [0]*n
#z[n-1] = n #문제에 따라 필요하다면 정의
#접미사가 일치하는 구간 중 왼쪽 끝점이 가장 왼쪽에 있는 구간 [left,right]
left = n-1
right = n-1
#n-2부터 0으로 역방향으로 순회
for i in range(n-2,-1,-1):
if i > left: #현재 인덱스 i가 [left,right]안에 있는 경우...
#z[i]를 z[i+n-1-right]와 i-left중 작은 값으로 시작할 수 있다.
z[i] = min(z[i+n-1-right], i-left)
#마지막 인덱스는 -1이므로, s[-z[i]-1]과 s[i-z[i]]가 일치하면 z[i]를 1씩 증가하는 방식으로
#가장 긴 접미사의 길이를 찾는다.
while i-z[i] >= 0 and s[-z[i]-1] == s[i-z[i]]:
z[i] += 1
#왼쪽 점은 i-z[i]이고 오른쪽 점은 i이므로, i-z[i]가 기존 left보다 작다면, 왼쪽으로 더 갔으므로 갱신
if i-z[i] < left:
left = i-z[i]
right = i
return z
이렇게 구한 z배열로 쿼리에 답하면 정답.. 쿼리는 1-based index니까 쿼리 i를 받을 때 z[i-1]에 접근해야한다는점 주의
6. 다른 풀이
문자열 s를 역으로 배열해서 가장 긴 공통 접두사의 길이가 원래 문자열 s의 가장 긴 공통 접미사의 길이가 될 것이다.
따라서 s를 역으로 배열하고 원래 구현한 z-function을 그대로 이용할 수 있다.
그리고 쿼리에는 반대로 답하면 될 것이다.
기존에는 z[i-1]을 출력했지만 역으로 배열한 이 경우에는 i = 1이라면 z[-1]을 출력해야할 것이고..
i = 2라면 z[-2]를 출력해야할 것이고... 즉 z[-i]를 출력해야한다.
from sys import stdin
def z_function(s):
n = len(s)
z = [0]*n
z[0] = n
left = 0
right = 0
for i in range(1,n):
if i < right:
z[i] = min(right - i, z[i-left])
while i + z[i] < n and s[z[i]] == s[i+z[i]]:
z[i] += 1
if i+z[i] > right:
left = i
right = i+z[i]
return z
s = stdin.readline().rstrip()[::-1]
z = z_function(s)
m = int(stdin.readline())
for _ in range(m):
i = int(stdin.readline())
print(z[-i])
참고
https://cp-algorithms.com/string/z-function.html#efficient-algorithm-to-compute-the-z-function
Z-function - Algorithms for Competitive Programming
Z-function and its calculation Suppose we are given a string $s$ of length $n$. The Z-function for this string is an array of length $n$ where the $i$-th element is equal to the greatest number of characters starting from the position $i$ that coincide wit
cp-algorithms.com
Z-function
길이가 $n$인 문자열 $s$가 있다. $1 \leq i \lt n$인 $i$에 대해 $z[i]$를 $i$에서 시작하는 suffix와 $s$의 가장 긴 common prefix의 길이라고 정의하자. 편의상 $z[0] = 0$이다. 이러한 $z$ 배열을 문자열 $s$의 Z-func
blog.myungwoo.kr
https://www.youtube.com/watch?v=wQwJhzR_4QU&t=472s
'알고리즘 > 문자열 알고리즘' 카테고리의 다른 글
| z function 활용법 2 - prefix이면서 suffix인 문자열을 찾는 방법- (0) | 2023.09.28 |
|---|---|
| z - function 활용법1 -패턴이 문자열에서 몇번이나 나왔는가? 찾는법- (0) | 2023.09.18 |
| suffix array 깊이 이해하기 2 -부분 문자열의 개수를 세는 방법- (0) | 2023.09.09 |
| suffix array 깊이 이해하기 1 -반복되는 부분 문자열 찾기- (0) | 2023.08.25 |
| 문자열 핵심 자료구조 suffix array O(NlogN) 최적화 배우기 (0) | 2023.08.17 |

