알고리즘 문제 해결(PS)을 위한 게임이론 기초지식 - 님 게임(Nim game) 배우기

1. 님 게임(Nim game)

 

게임이론에서 가장 중요한 게임 형태중 한가지라고 할 수 있다.

 

""수학적 전략 게임으로, 여러 개의 돌 무더기가 있다고 가정하자.

 

두 사람이 서로 차례를 번갈아가며 게임을 한다.

 

자신의 차례에 하나의 돌 무더기를 선택하고, 1개이상의 원하는 만큼의 돌을 제거한다.

 

마지막 남은 돌을 제거하는 사람이 게임에서 승리한다.""

 

 

2. 게임의 수학적 기술

 

현재 시점에 n개의 돌 무더기에 있는 돌의 개수가 $x_{1}, x_{2}, ... , x_{n}$이라고 하자.

 

내가 어떤 돌 무더기를 하나를 선택하여 돌을 가져가고 나서 변화된 돌의 개수는 $y_{1}, y_{2}, ... , y_{n}$이라고 하자.

 

만약 k번째의 돌 무더기를 선택하고 돌을 가져갔다면.. 돌의 개수는 줄어드니까 $i = k$에서 $x_{i} > y_{i}$이고,

 

가져가지 않은 돌 무더기라면, $i \neq k$이면, $x_{i} = y_{i}$이다.

 

다음, s는 현재 돌무더기의 돌의 개수를 모두 xor한 값 $s = x_{1} \oplus x_{2} \oplus ... \oplus x_{n}$이고,

 

t는 k번째 돌 무더기에서 돌을 가져가고 나서 변화된 돌의 개수를 모두 xor한 값 $t = y_{1} \oplus y_{2} \oplus ... \oplus y_{n}$이다.

 

---------------------------------------------------------------------------------------------------------------

 

**xor연산 성질

 

1) xor의 항등원은 0이다.

 

그러니까 0과 x를 xor연산하면 x이다.

 

2) xor연산은 교환법칙이 성립하고, 결합법칙이 성립한다.

 

즉 $a \oplus b = b \oplus a$이고 $a \oplus (b \oplus c) = (a \oplus b) \oplus c)$

 

3) XOR의 역원은 XOR이다. 

 

즉, 자기자신끼리 xor연산하면 0이다. $x \oplus x = 0$이다.

 

---------------------------------------------------------------------------------------------------------------------------------------------------

 

그러면 이제.. $t = 0 \oplus t$이다. 왜냐하면 0과 자기자신 t를 xor연산하면 자기자신이기 때문이다.

 

그리고 $0 = s \oplus s$이다. 자기자신끼리 xor연산하면 0이기 때문이다.

 

그러므로, $t = s \oplus s \oplus t$이다.

 

여기서 $s = x_{1} \oplus x_{2} \oplus ... \oplus x_{n}$이고, $t = y_{1} \oplus y_{2} \oplus ... \oplus y_{n}$이다.

 

그러므로, $$t = s \oplus (x_{1} \oplus x_{2} \oplus ... \oplus x_{n}) \oplus (y_{1} \oplus y_{2} \oplus ... \oplus y_{n})$$

 

--------------------------------------------------------------------------------------------------------------------------------

 

4) $(a \oplus b) \oplus (c \oplus d) = ((a \oplus b) \oplus c) \oplus d =  a \oplus (b \oplus c) \oplus d = a \oplus (c \oplus b) \oplus d = (a \oplus c) \oplus (b \oplus d)$

 

교환법칙과 결합법칙을 이용해 위 식을 증명할 수 있다. 

 

---------------------------------------------------------------------------------------------------------------------------------

 

4)를 이용하면, t는 다음과 같이 쓸 수 있을 것이다.

 

$$t = s \oplus (x_{1} \oplus y_{1}) \oplus (x_{2} \oplus y_{2}) ... \oplus (x_{k} \oplus y_{k}) \oplus ... (x_{n} \oplus y_{n})$$

 

여기서 k는 내가 선택한 돌무더기의 번호이다.

 

그러므로 $x_{k} > y_{k}$이고, $i \neq k$인 모든 i에 대하여 $x_{i} = y_{i}$이다.

 

자기자신끼리 xor연산은 0이고 0과 xor 연산하면 자기자신이 나오므로... 

 

$$t = s \oplus 0 \oplus 0 \oplus ... (x_{k} \oplus y_{k}) ... \oplus 0 = s \oplus x_{k} \oplus y_{k}$$

 

3. 필승전략

 

두 사람이 모두 최선의 방법으로 게임할때, 반드시 이기는 방법이 존재한다

 

"각 돌무더기에 있는 돌의 개수를 xor 연산하여, 값을 0으로 만들 수 있도록 돌을 적절하게 가져간다면 게임을 반드시 이긴다"

 

돌을 적절히 가져가서, 항상 돌 무더기의 돌의 개수를 모두 xor 연산한 값이 0이 되도록 다음 차례로 넘겨준다면, 게임을 반드시 이길 수 있다.

 

 

4. 증명

 

1) 현재 자기 차례에 돌 무더기의 돌의 개수를 xor한 값 s = 0이라고 한다면,

 

내가 돌을 어떻게 가져가더라도, 돌을 가져가고 나서 남은 돌 무더기의 돌의 개수를 xor한 값 t는 0이 아니다.

 

먼저 돌이 아예 없다면.. 즉 모든 i에 대해 $x_{i} = 0$이라면.. 이미 게임의 승패가 결정되었으니 의미 없다. 

 

내가 돌을 가져갈 수 있는 상태에서, s = 0이라고 하자. 

 

그리고 k번째 돌무더기를 선택하여 돌을 가져갔다고 한다면..

 

$$t = s \oplus x_{k} \oplus y_{k} = 0 \oplus x_{k} \oplus y_{k} = x_{k} \oplus y_{k}$$

 

여기서 $x_{k} > y_{k}$이므로, t는 0이 아니다.

 

 

2) 이번엔 s가 0이 아니라고 하자.

 

그러면 다음 차례에 돌무더기의 돌의 개수를 모두 xor한 값 t를 0으로 만들 수 있도록 가져가는 방법의 수가 반드시 존재한다.

 

 

s를 2진법으로 나타내서 제일 왼쪽에 존재하는 1의 자리를 d라고 하자. 

 

예를 들어 $s = 00101101_{2}$이면 d = 6이다.

 

s가 0이 아니기 때문에 d가 반드시 존재한다. 

 

이제 $x_{1}, x_{2}, ... , x_{n}$에 대하여 이들을 2진수로 모두 바꿀때, d번째 자리의 수가 1인 $x_{k}$를 고르자.

 

이러한 $x_{k}$는 반드시 존재하는데, 존재하지 않는다고 가정한다면,

 

모든 $x_{i}$의 d번째 자리가 0인데.. 모든 $x_{i}$를 xor한 값 s의 d번째 자리가 1이므로 모순이다. 

 

왜냐하면 모든 0을 xor하면 0이어야하는데 d가 1이니까 모순

 

이제 $y_{k} = s \oplus x_{k}$라고 가정하자.

 

그러니까 $x_{k}$에서 어떤 수만큼 돌을 가져가서 $y_{k}$로 만드는데,

 

그러한 $y_{k} = s \oplus x_{k}$으로 만드는 방법이 반드시 존재한다는 것을 보인다.

 

s의 제일 왼쪽에 존재하는 1의 자리가 d이고, $x_{k}$도 마찬가지이므로, d번째 이전의 자리는 모두 0이다.

 

따라서 둘을 xor한 결과 $y_{k}$도 마찬가지로 d자리 왼쪽은 0으로 전부 똑같다.

 

그리고, s의 d번째 자리가 1이고 $x_{k}$도 d번째 자리가 1이라고 가정했으므로, 동일한 1을 xor한 결과인 $y_{k}$의 d번째 자리는 0이다.

 

즉, $x_{k}$와 $y_{k}$의 차이는 많아야 $2^{d}$이다.

 

그리고 d번째 자리 오른쪽으로는 아무리 차이나봐야 $2^{d-1} + 2^{d-2} + ... + 2^{0}$이다. 

 

이는 공비가 2이고 초항이 1이며 항 수가 d개인 등비수열의 합 $2^{d} - 1$과 같다.

 

 

 

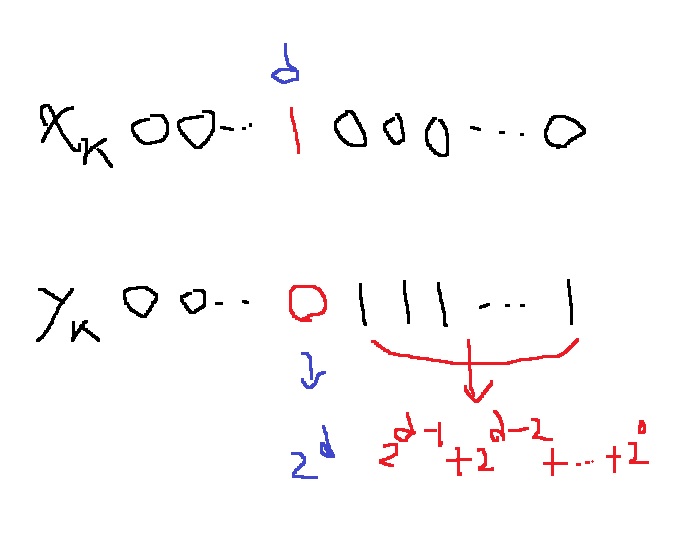
따라서 $x_{k}$와 $y_{k}$는 차이가 최소한 1이상이다.

 

그러므로 $x_{k}$개가 존재하는 k번째 돌 더미에서 반드시 $y_{k} = s \oplus x_{k}$가 되도록 가져가는 돌의 개수가 존재한다.

 

또한 그렇게 돌을 가져간다면...

 

$$t = s \oplus x_{k} \oplus y_{k} = s \oplus x_{k} \oplus (s \oplus x_{k}) = 0$$ 으로 만들 수 있다.

 

즉, 다음 차례에 돌 무더기의 돌의 개수를 xor한 값 t = 0으로 반드시 만들 수 있다.

 

 

3) 게임의 필승 전략은 돌을 적절히 가져가서 돌무더기 돌의 개수를 xor한 값이 0이 되도록 다음 차례로 넘겨준다면, 게임을 반드시 이긴다.

 

위에서 증명한 두가지 사실을 이용한다면..

 

자기 차례에 현재 존재하는 돌무더기의 돌의 개수를 xor한 값 x = 0이라면, 어떻게 하더라도, 다음 차례에 x가 0이 아니므로 게임을 이길 수 없다. 

 

반대로 x가 0이 아니라면, 다음 차례에 반드시 x는 0으로 만들 수 있고, 그러므로 최선의 방법으로 플레이할때, 반드시 게임을 이길 수 있다.

 

 

5. 연습문제

 

11868번: 님 게임 2 (acmicpc.net)

11868번: 님 게임 2

 

6. 풀이

 

제시하는 게임은 정확히 님 게임의 원본이고..

 

님 게임의 필승전략을 안다면, 아주 쉽게 풀 수 있다.

 

현재 존재하는 돌무더기의 돌의 개수를 xor해서 0이라면 첫 시작인 사람이 게임을 지고,

 

0이 아니라면 첫 시작인 사람이 게임을 이긴다.

 

from sys import stdin

n = int(stdin.readline())

A = list(map(int,stdin.readline().split()))

z = A[0]

for i in range(1,n):
    
    z ^= A[i]

if z == 0:
    
    print('cubelover')

else:
    
    print('koosaga')

 

참고

 

 

https://m.blog.naver.com/PostView.naver?isHttpsRedirect=true&blogId=oidoman&logNo=221145674383

XOR의 마법

 

https://accu.org/journals/overload/20/109/lewin_1915/

All About XOR

 

https://stackoverflow.com/questions/14279866/what-is-inverse-function-to-xor

What is inverse function to XOR?

 

https://math.stackexchange.com/questions/2972675/inverse-operation-of-xor

Inverse operation of xor

 

https://librewiki.net/wiki/%ED%95%84%EC%8A%B9_%EC%A0%84%EB%9E%B5_%EA%B2%8C%EC%9E%84

필승 전략 게임

 

https://blog.myungwoo.kr/27

Nim game