1. 이분 탐색(binary search)
False 구간, True 구간 2개의 partition으로 분할된 구간에서, 분할 경계의 위치를 O(logN)에 찾는 알고리즘이다.
STL로 구현된 lower_bound와 upper_bound는 가장 유명한 이분 탐색 함수중 하나이다.
정렬된 배열에서 x의 lower bound는 정렬 상태를 유지한 채 x를 삽입할 수 있는 첫번째 위치이고 upper_bound는 마지막 위치이다.

위 그림에서 lower_bound(20)은 20을 넣을 수 있는 첫번째 위치로, 1번에 넣을 수 있다..
upper_bound(20)은 20을 넣을 수 있는 마지막 위치로, 4번에 넣을 수 있다..(원래 4번은 5번으로 이동하겠지)
이분 탐색적 설명으로는, lower_bound는 x보다 크거나 같은 원소의 첫번째 위치이며,
upper_bound는 x보다 큰 원소의 첫번째 위치이다.
--------------------------------------------------------------------------------------------------------------------------------------------------
주어진 배열에 대해, 배열의 값이 x이상인지, x보다 큰지에 따라 배열을 False/True 두 partition으로 나눌 수 있다.

lower_bound, upper_bound 모두, True인 첫번째 위치를 찾으면 된다.
---------------------------------------------------------------------------------------------------------------------------------------------------
2. 파이썬 라이브러리
파이썬에서는 이진 탐색을 쉽게 구현할 수 있도록 bisect 라이브러리를 제공
bisect 라이브러리는 "정렬된 배열"에서 특정한 원소를 찾아야 할때 매우 효과적으로 사용된다.
bisect_left()함수와 bisect_right()함수가 핵심이다.
두 함수 모두 O(logN)에 동작한다.
2-1) bisect_left(a,x)
정렬된 순서를 유지하면서, 리스트 a에 x를 삽입할때, 가장 왼쪽 인덱스를 찾아준다.
정렬된 a에 정렬 순서를 유지한채로 x를 넣을 수 있는 첫번째 위치
2-2) bisect_right(a,x)
정렬된 순서를 유지하면서, 리스트 a에 x를 삽입할때, 가장 오른쪽 인덱스를 찾아준다.
정렬된 a에 정렬 순서를 유지한채로 x를 넣을 수 있는 마지막 위치
예를 들어 다음과 같이 [1,2,4,4,8]로 정렬된 배열이 있다면.. 데이터 4를 넣을려고 할때
bisect_left(a,4)는 2를 반환하고
bisect_right(a,4)는 4를 반환한다.


간단한 응용으로 "값이 특정 범위에 속하는 원소의 개수"를 bisect 함수를 이용해 쉽게 구할 수 있다.
당연히 배열은 정렬되어 있어야한다.
다음 함수는 [left_value,right_value]에 속하는 원소의 개수를 O(logN)에 반환한다.
from bisect import bisect_left, bisect_right
#값이 [left_value, right_value]인 데이터의 개수를 반환
def count_by_range(a,left_value,right_value):
right_index = bisect_right(a,right_value)
left_index = bisect_left(a,left_value)
return right_index - left_index
a = [1,2,3,3,3,3,4,4,8,9]
print(count_by_range(a,4,4))
print(count_by_range(a,-1,3))
2
6
3. 첫번째 True를 찾기
False,False,...,True,True,..로 정렬된 배열에서
min이상 max이하인 구간에서, f(i) = True인 첫번째 i를 찾는 코드는..
#f(i) = True인 첫번째 i를 찾는 함수
#만약 [min,max]모두 False라면 max+1을 return하도록
def first_true(min,max):
start = min
end = max + 1
while (start != end):
#mid를 (start+end)//2로 구하는 경우가 있는데, 비추천
#오버플로우가 일어날 수 있으며(파이썬은 예외지만..)
#start+end가 음수일 경우 //2(2의 몫을 구하는)가 다르게 동작함
mid = start + (end - start)//2
#현재 mid가 True라면, end를 mid로
#False라면 start를 mid+1로
if f(mid) == True:
end = mid
else:
start = mid + 1
return start
여기서 몇가지 포인트는
mid 포인트를 (start+end)//2가 아니고, start+(end-start)//2로 구한다는 점이다.
파이썬이야 오버플로우 걱정이 없기는 한데 다른 언어에서는 오버플로우가 일어날 수도 있다고 한다
---------------------------------------------------------------------------------------------------------------------------------------------
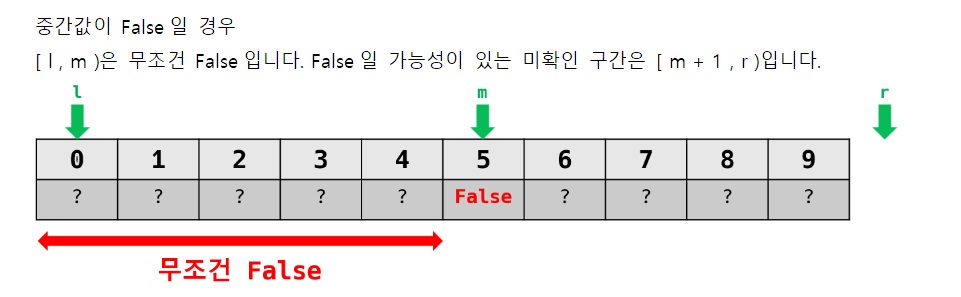
만약 정렬된 배열에서 f(mid)가 True라면..?
mid+1부터 end-1까지는 모두 True이다.

그러므로 end를 mid로 옮겨준다.
그래서 [start~end)를 검사하면 된다.
mid도 확실히 True인데, 왜 end = mid - 1로 안옮기냐고??
지금 그림을 보면 [start~end)를 검사하고 있잖아
그것처럼 end 포인트를 mid에 옮기면... 검사해야할 구간이 반열린구간 [start,end)로 되니까..
처음 상황과 동일한 부분 문제가 된다.
mid - 1로 옮기면 검사해야할 구간이 [start,end-1]이 되어버려서... 문제가 생길 수 있다
------------------------------------------------------------------------------------------------------------------------------
f(mid)가 False라면? start부터 mid까지는 False이므로...
정렬된 배열이니 start부터 mid까지는 반드시 False이다.
따라서 다음 검사해야할 구간은.. [mid+1,end)가 되어, start를 mid+1로 옮겨준다.
4. lower bound
위 방식대로, x보다 크거나 같은 첫번째 위치를 찾는 lower bound함수는...
#x보다 크거나 같은 첫번째 위치를 찾는 함수
def lower_bound(start,end,x):
while(start != end):
mid = start + (end-start)//2
#mid+1~end-1까지는 모두 x이상이므로...
#x보다 크거나 같은 첫번째 위치는 [start,mid)에 존재한다.
if mid >= x:
end = mid
else:
start = mid + 1
return start
mid >= x이면, mid 이후에는 모두 x보다 크거나 같으므로... x보다 크거나 같은 "첫번째 위치"는 mid+1이후에는 없다
[start,mid]에 존재할 가능성이 있으므로, end를 mid로 옮겨준거고
mid < x이면, mid 이전에는 모두 x보다 작으므로, [mid+1,end)에 x보다 크거나 같은 첫번째 위치가 존재할 수 있다.
따라서 x보다 크거나 같은 "첫번째 위치"는 start = mid+1 이후에 존재할 수 있으니 start를 mid+1로 옮긴거
그래서 항상 "첫번째 위치"는 start에 존재하니 start를 return
5. upper bound
정렬된 배열에서 x보다 큰 첫번째 위치를 찾는 upper bound 함수는....
def upper_bound(start,end,x):
while (start != end):
mid = start + (end - start)//2
#mid가 x보다 크다면...
#mid+1부터 end-1까지 모두 x보다 크므로...
#x보다 큰 "첫번째 위치"는 mid+1 이후에는 존재하지 않고 [start,end]에 존재
if mid > x:
end = mid
else:
start = mid + 1
return start
마찬가지로, mid > x이면... mid + 1부터 end-1까지는 모두 x보다 크다.
x보다 큰 "첫번째 위치"는 mid+1이후에는 존재하지 않는다.
따라서 [start,mid]에 존재할 수 있으니 end를 mid로 옮겨준다.
반대로 mid <= x이면... mid 이하는 모두 x보다 작거나 같다.
x보다 "큰" "첫번째 위치"는 mid+1 이후에 존재할 수 있으므로... start를 mid+1로 옮긴다.
따라서 항상 start에 "첫번째 위치"가 존재한다.
그래서 start를 return
6. f(i) = True인 마지막 위치
배열이 True/False로 두 partition으로 나뉠때, f(i) = True인 마지막 위치는 어떻게 찾을 수 있을까?
위의 사고를 조금 응용하면 가능하겠지
#f(i) = True인 마지막 위치 i를 return
#[min,max]가 전부 False이면 min-1을 return
#True,True,...,False,False,..로 정렬
def last_true(min,max):
start = mid-1
end = max
while (start != end):
mid = end - (end - start)//2
if f(mid) == True: #mid이전은 모두 True이니.. start를 mid로 옮겨 마지막 위치를 찾으러
start = mid
else: #mid 이후가 모두 False이므로.. end를 mid-1로 옮겨 start~mid-1에서 마지막 True찾으러
end = mid - 1
return start
7. 권장하는 구현 방식
이분 탐색은 구현하는 방법이 사람마다 다양하다.
가급적이면 배열의 길이가 n일때 탐색 구간을 0~n-1로 하는 것이 아니라,
1) end에 1을 더해 0~n으로 하는 반열린 구간 [start,end)로 하는 것을 권장
2) 전체 구간 설정을 잘못하거나 start,end를 잘못 옮겨서 구간을 쪼개는 과정에 무한 루프가 일어날 수 있다.
이분 탐색은 3) 배열의 전체 구간을 이분법적으로 나눠서 탐색하는 과정이 올바른 사고방식이다.
array[mid] > target, array[mid] < target, array[mid] == target으로 3가지 경우로 나눠서 탐색하는 것은 이분탐색이 아니다.
8. 반드시 이분탐색이 유리한가
이분탐색의 시간복잡도는 O(logN)이고, 순차탐색의 시간복잡도는 O(N)이다.

N이 크면 클수록 둘의 차이가 두드러진다.
하지만 이분탐색이 반드시 유리한 것은 아니다.
이분탐색은 배열이 반드시 정렬되어있어야 올바르게 동작한다.
정렬되어 있지 않다면, 정렬을 하기 위한 추가적인연산이 필요하다.
특수한 상황이 아니면 일반적으로 가장 빠른 정렬 연산의 시간복잡도는 O(NlogN)이다.
따라서 정렬되어 있지 않다면, 이분탐색은 O(NlogN) + O(logN)의 시간복잡도가 필요하지만, 순차탐색은 여전히 O(N)이다.
그래서 오히려 순차탐색에 비해 느려진다.
따라서 이분탐색을 사용하기 전에, 정렬되어 있지 않다면 한번 더 생각해보아야 한다.
'알고리즘 > 이분 탐색' 카테고리의 다른 글
| 이분탐색 올바른 사고 연습하기 1편 (0) | 2023.04.01 |
|---|---|
| 처음 배우는 parametric search 이해해보기 (0) | 2023.03.29 |
| 이분탐색 응용력 키우기 연습1 -차이가 가장 가까운 값을 찾는 방법- (0) | 2023.03.28 |
| 이분탐색을 이용해서 MN개의 조합에서 k번째 수를 찾는 놀라운 방법 (0) | 2023.03.21 |
| 이진 탐색 정복 -array를 쓰지 않아도 되는 경우- (0) | 2022.09.18 |

