1. 좌표, 기하학을 숫자로 바꾸다
17세기 이전까지 수학은 크게 기하학과 대수학으로 나뉘었습니다.
원의 넓이 같은 도형의 성질을 다루는 수학이 기하학이고, 2차방정식 같이 문자와 수를 다루는 수학이 대수학이죠.
이전까지는 둘을 서로 다른 영역으로 취급했습니다.

그러던 어느 날, 르네 데카르트는 침대에 누워 있다가 천장에 붙어 있는 파리를 보았습니다.
그리고 재미있는 생각을 떠올렸습니다.
'어떻게 하면 파리가 천장의 어느 위치에 붙어있는지, 정확하게 표현할 수 있을까?'
그리고 데카르트는 좌표(coordinates)라는 개념을 고안합니다.
이는 서로 다른 분야로 여겨지던 기하학과 대수학의 개념을 하나로 합쳐낸 혁신적인 발상이었습니다.
데카르트는 좌표의 개념을 <방법서설>에 공개합니다.
이 책에는 '나는 생각한다. 고로 존재한다'라는 명언도 실려있었지만, 부록으로 좌표라는 수학사에 길이 남을 엄청난 개념 또한 함께 실려 있었습니다.
데카르트가 기하학과 대수학의 관계를 밝혀내자, 수학자들은 엄청난 충격을 받았습니다.
좌표의 발명은 이후 수학사에 지대한 영향을 끼치죠.
2. 기하학과 대수학은 무슨 차이가 있나?
그렇다면 기하학과 대수학은 어떤 차이가 있을까요?
$$\frac{1}{2} + \frac{1}{4} + \frac{1}{8} + ... = 1$$을 어떻게 증명할 수 있을까요?
기하학으로는 다음과 같이 크기 1인 정사각형을 절반씩 나누어서 증명할 수 있습니다.
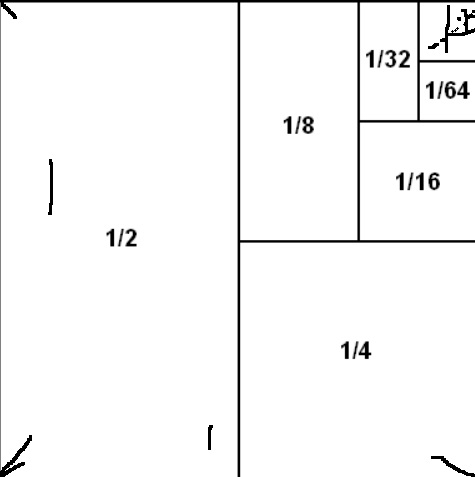
대수학적으로는 다음과 같이 무한등비급수의 합을 이용해서 증명할 수 있습니다.
$$\frac{1}{2} + \frac{1}{4} + \frac{1}{8} + ... = \sum_{n=1}^{\infty}(\frac{1}{2})^{n}=\frac{1}{2}\frac{1}{1-\frac{1}{2}} = 1$$
어느 쪽이 더 쉬워보이나요? 사람에게는 기하학적으로 증명하는 것이 더 쉬워보입니다.
아무래도 대수적으로 증명하는 방식은 직관적이지 않죠.
몇개 선을 긋고 그 크기를 눈으로 직접 비교해서 이해하는 방식이 훨씬 더 이해하기 쉽습니다.
그렇다면 컴퓨터는 어떨까요? 컴퓨터가 기하학을 눈으로 인지하고 사람처럼 직관으로 그 크기를 비교할 수 있나요?
기하학 증명을 컴퓨터에게 가르칠 수 있나요?
사람에게는 쉽지만, 컴퓨터에게는 어려운 '모라벡의 역설'을 얘기한 바 있습니다.
기하학을 이해하는 일은 모라벡의 역설에 해당합니다.
사람은 기하학을 직관으로 쉽게 이해할 수 있지만, 컴퓨터는 그림을 이해하는 게 엄청나게 어려운 일이죠.
그렇다면 대수적 증명은 어떨까요?
사람에게 수식을 풀어서 증명하는 일은 매우 어렵고 까다롭지만 컴퓨터가 가장 잘하는게 이런 일입니다.
컴퓨터는 숫자로만 표현할 수 있다면 무엇이든 해낼 수 있습니다.
3. "스위치로 이루어진 모든 전기 회로는 True/False로 표현할 수 있다"
미국의 수학자 클로드 섀넌은 MIT의 대학원생 시절 이진법을 이용해 모든 계산을 할 수 있다는 디지털 논리회로의 개념을 고안합니다.

"스위치로 이루어진 전기 회로는 bool logic으로 표현할 수 있다"
이 논문은 20세기 가장 위대한 석사 논문이라는 찬사를 받았고, 이후 섀넌은 디지털의 아버지로 추앙받습니다.
그의 논문은 이후 정보 이론이라는 새로운 학문을 탄생하게 했고, 마침내 세상은 정보통신의 시대로 접어들게 됩니다.
섀넌 덕분에 컴퓨터는 0과 1, 단 2개의 숫자로 모든 계산을 해낼 수 있게 되었고, 정보의 개념을 수학적으로 정의할 수 있게 되었죠.
그리고 우리는 이 단위를 비트(bit)라고 부릅니다.
오늘날 32비트, 64비트라고 일컫는 바로 그 비트를 말합니다.
4. 언어를 수로 표현한다는 것은 무슨 뜻인가
- 데카르트의 좌표 덕분에 기하학을 방정식과 숫자로 표현할 수 있게 되었다.
- 섀넌의 디지털 논리회로와 정보 이론 덕분에 컴퓨터는 모든 정보와 숫자를 계산할 수 있게 되었다.
실제로 현대 수학에서는 좌표를 이용해 추상적인 기하학을 수로 표현하는 것을 매우 중요하게 생각합니다.
컴퓨터에 계산을 맡길 수 있기 때문입니다.
그렇다면 처음의 질문으로 돌아가봅시다.
"컴퓨터가 유사한 단어를 판별하려면 어떻게 해야할까요?"
추상적인 인간의 언어도 명료하게 표현해낼 수만 있다면 마찬가지로 컴퓨터가 계산할 수 있지 않을까요?
인간의 언어를 수로 표현한다면 어떨까요?
추상적인 언어를 구체적인 숫자로 표현할 수 있다면 컴퓨터가 계산을 해낼 수 있을겁니다.
그렇다면 언어를 숫자로 어떻게 표현해야할까요?
단어를 숫자로 표현한다는 것은 단어가 갖는 의미에서 각각의 특징을 추출해 수치화하는 과정입니다.
그래서 단어의 의미가 비슷하다는 것을 숫자로 표현한 값이 얼마나 가까운지로 판별할 수 있게 되는 거죠.
이처럼 숫자로 표현하는 것을 자연어 처리 분야에서는 언어를 벡터로 표현한다고 말합니다.
벡터는 공학에서 방향과 크기를 나타내는 값인데 마치 기하학을 좌표로 명료하게 표현하는 것과 비슷합니다.
이처럼 단어의 의미를 벡터로 표현하면 단어가 유사한 정도를 구체적인 수치로 나타낼 수 있으므로,
유사도뿐만 아니라 다양한 과제에 응용하기 편리합니다.
무엇보다 모든 것이 숫자이기 때문에 계산이 쉽죠.
컴퓨터는 추상적인 무언가를 논리적이지 않은 방식으로는 계산할 수 없습니다.
하지만 구체적인 숫자를 계산하는 일은 컴퓨터가 가장 잘하는 일이죠.
뿐만 아니라 데이터가 많을수록 계산은 더욱 정교해집니다.
게다가 이 과정을 자동으로 처리할 수 있다면, 엄청난 이점이 생기겠죠.
이처럼 언어를 벡터로 표현하는 방식에는 장점이 많기 때문에 단어와 단어 간의 관계를 다양한 벡터로 계산하는 연구를 지금도 활발하게 진행하고 있습니다.

'책 읽기 > 비전공자도 이해할 수 있는 AI지식' 카테고리의 다른 글
| 비전공자도 이해할 수 있는 AI지식 -기계와 대화할 수 있을까- (0) | 2022.12.29 |
|---|---|
| 비전공자도 이해할 수 있는 AI지식 -구글은 어떻게 언어를 숫자로 바꿨는가- (0) | 2022.12.27 |
| 비전공자도 이해할 수 있는 AI지식 -컴파일러, 인간의 언어를 이해하다- (0) | 2022.12.21 |
| 비전공자도 이해할 수 있는 AI지식 -이루다는 왜 2주만에 서비스를 멈췄는가- (0) | 2022.12.19 |
| 비전공자도 이해할 수 있는 AI지식 -외국어를 공부안해도 되는 시대는 올 수 있을까- (0) | 2022.12.17 |

