1. 문제
크기가 N인 정수의 배열 A가 주어지며 구간의 합을 구하는 문제를 M번 수행하는 문제에서
중간에 index번째 수를 value로 바꾸는 문제는 세그먼트 트리를 이용하여 해결했다.
이번엔 단순히 i번째 수를 value로 바꾸는 것이 아니라, i번째 수부터 j번째 수에 v를 더하는 경우를 생각해보자.
세그먼트 트리에서 index번째 수를 value로 바꾸는 연산은 O(logN)인데,
i번째수부터 j번째 수를 모두 v로 바꾼다면 최대 O(NlogN)이다.
하지만 그냥 i번째 수부터 j번째 수를 순회해서 바꾸면 O(N)이다. 세그먼트 트리를 사용했더니 오히려 더 느리게 된다
2. 구간을 변경하는 update함수
[left,right]의 모든 수에 value를 더하는 작업을 수행해야한다면?
[left,right]가 [start,end]를 벗어나면 변경하지 않고 return하고
리프노드를 만나면, 그러니까 start = end인경우, tree_index에 저장된 값에 value를 더해주고
리프노드가 아니라면, 왼쪽, 오른쪽으로 나누어서 탐색에 들어간다.
이미 리프노드에서 return되면서 자식 값들이 모두 변경되어 있고, 이를 이용해서
부모로 올라오면서 부모 값들에 합을 저장하면서, 자연스럽게 변경시켜준다
#[left,right]의 모든 수에 value를 더한다
def update_range(tree,tree_index,start,end,left,right,value):
#구간을 벗어나면, 변경하지 않는다
if left > end or right < start:
return
#리프노드를 만나면, value를 더해준다.
if start == end:
tree[tree_index] += value
return
#리프노드가 아니면, 왼쪽,오른쪽으로 나누어 들어간다.
#변경된 리프노드값에서 return되면서, 자식부터 부모로 변경된 값들이 올라와 부모가 변경
mid = (start+end)//2
update_range(tree,2*tree_index,start,mid,left,right,value)
update_range(tree,2*tree_index+1,mid+1,end,left,right,value)
tree[tree_index] = tree[2*tree_index] + tree[2*tree_index+1]
효율적으로 보여도 left부터 right까지 모든 수를 변경시키므로 O(NlogN)이다.
3. 예시로 이해하는 lazy propagation
배열 A가 다음과 같은 경우를 생각해보자.
| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| A[i] | 3 | 6 | 2 | 5 | 3 | 1 | 8 | 9 | 7 | 3 |
이를 이용해 세그먼트 트리를 만들면 다음과 같다.
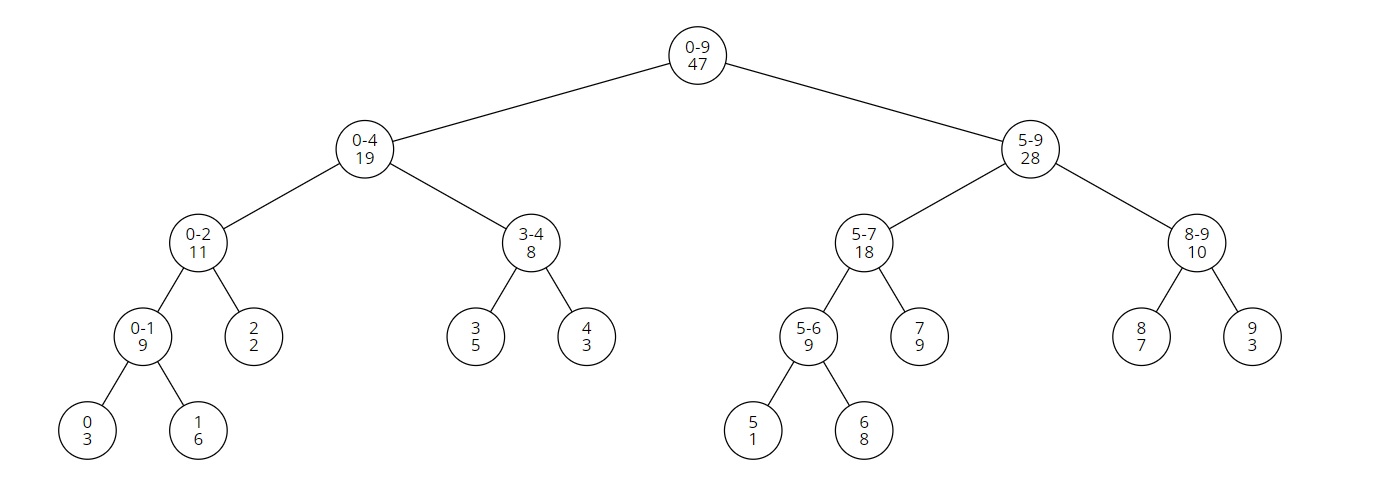
이제 [3,7]에 2를 더해야하는 경우를 생각해보자.
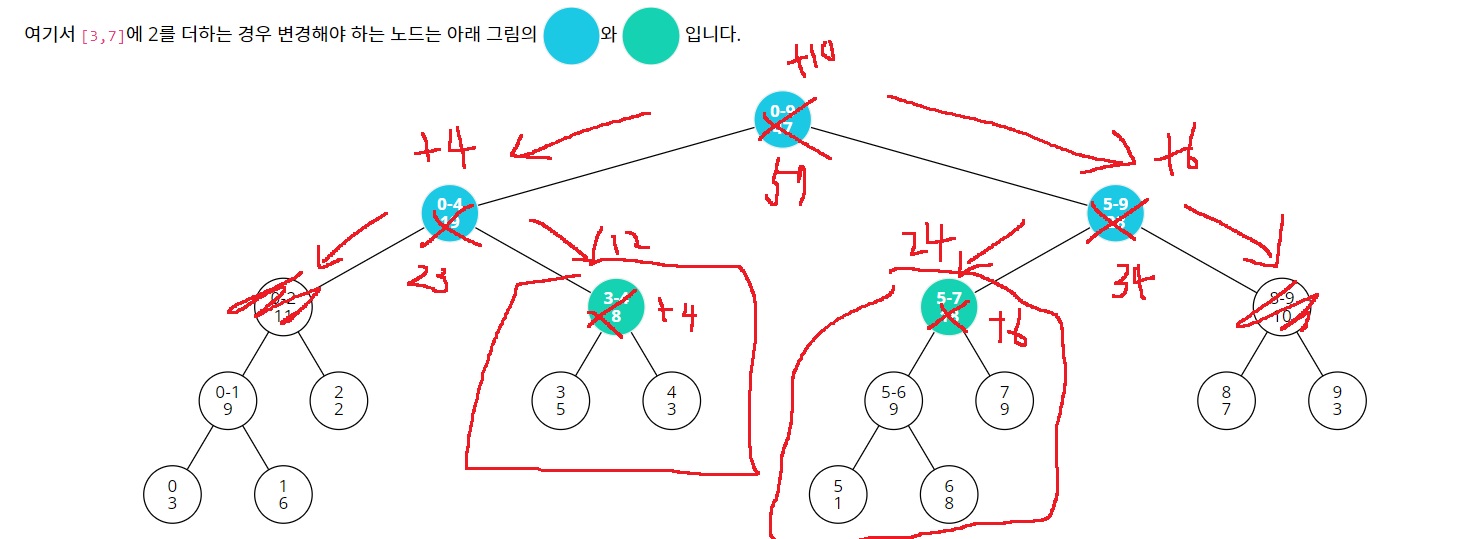
세그먼트 트리의 update함수처럼 루트노드부터 탐색을 진행해서, [start,end]가 [left,right]에 벗어나지 않는 노드들을 모두 찾아간다.

벗어나는 경우는 더 이상 탐색하지 않고, 단순히 return(빨간색)
[left,right]안에 [start,end]가 완전히 포함되는 경우는 초록색
[start,end]와 [left,right]가 일부에 포함되는 경우가 파란색
파란색인 경우는 일반적인 세그먼트 트리에서 update 처리하던 것처럼 왼쪽, 오른쪽으로 나누어 들어가 탐색을 진행하지만,
[left,right]안에 [start,end]가 완전히 포함되는 초록색은 조금 특별하게 처리해야한다.
----------------------------------------------------------------------------------------------------------------------------------------------
3-1) lazy
lazy는 나중에 변경해야하는 값을 저장하는 배열이다.
[3,4]의 합을 저장하는 노드에 대응하는 lazy[i]에 10이 저장되어 있다면, A[3]과 A[4]에 10을 더해줘야하는데,
나중에 10을 더하겠다는 의미를 가진다.
-----------------------------------------------------------------------------------------------------------------------------------------------

초록색 노드가 루트인 서브트리들의 노드들은 모두 [3,7]에 포함되는 노드들로, 값을 변경해야하는 노드들이다.
이런 노드들의 변경은 "나중에 필요할때 하기로"하며 그 값들을 lazy배열에 저장해두는 것이 핵심이다.
[3,7]의 구간에 2를 더해준다고 해보자.
초록색을 만나기 전인 파란색에는 해당 구간의 모든 수에 2를 더해주고,
초록색을 만나면, 초록색 노드에 구간의 모든 수에 2를 더해준 다음에,
초록색의 자식 노드에는 lazy배열에 2를 더해준다
그러면, [0,9]에는 [3,7]이 3,4,5,6,7 5개 있으니 10이 더해질거고
[0,4]에는 [3,7]이 3,4 2개 있으니 4가 더해질거고
[5,9]에는 [3,7]이 5,6,7 3개 있으니 6이 더해질건데

그러면 초록색 노드에 오면..
[3,4]에는 [3,7]이 2개 있으니 4를 더해주고, [5,7]에는 5,6,7 3개 있으니 6을 더해서..
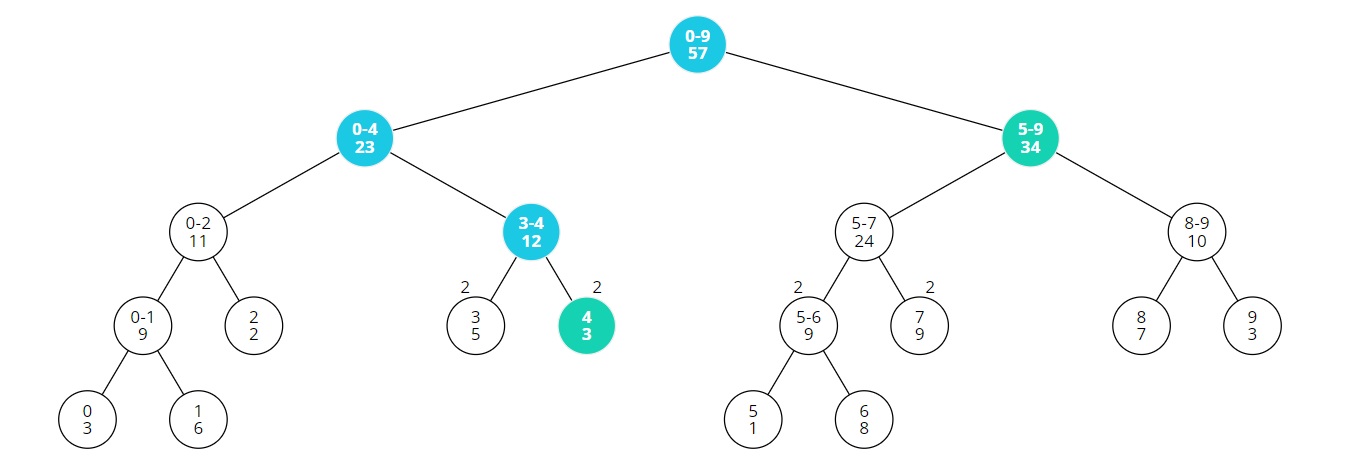
일단 바뀔건데... 초록색 노드 아래의 자식 노드들에도 값을 변경했었지만..
이제는 lazy배열에 저장해두고, 나중에 필요할때 값을 변경하는게 목표다.

따라서 [3,7]의 구간에 2를 더해주면 현재 세그먼트 트리는 위와 같고, A배열은 다음과 같이 바뀔거다
| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| A[i] | 3 | 6 | 2 | 5 | 3 | 1 | 8 | 9 | 7 | 3 |
| +2 | 3 | 6 | 2 | 7 | 5 | 3 | 10 | 11 | 7 | 3 |
lazy propagation에서는 어떤 노드를 방문할때마다, lazy배열에 값이 존재하는지 체크를 한다.
lazy값이 0이 아닌 경우에는 해당 노드에 저장된 합을 변경해주고, 자식 노드에게 lazy값을 전달해준다.
그런데 lazy배열에는 그 노드가 담당하는 구간의 각각의 수에 더해야하는 값이 저장되어 있다.
그러니까 위 그림에서 [5,6]에는 lazy에 2가 저장되어있는데, 실제로는 2만 더해주는게 아니라 5번째 원소와 6번째 원소 각각에 2를 더해줘야하니 총 4를 더해줘야한다.
그러므로 각 노드에 lazy배열의 값에 그 구간에 포함된 수의 개수만큼 곱해서 더해준다.
"그 구간에 포함된 수의 개수"는 어떻게 구해?
만약 해당 노드가 담당하는 구간이 [start,end]라고 한다면, tree[tree_index]에는 lazy[tree_index]*(end-start+1)을 더해준다.

다시 위 상황에서 [4,9]에 1을 더한다고 해보자. 어떻게 할 수 있을까?
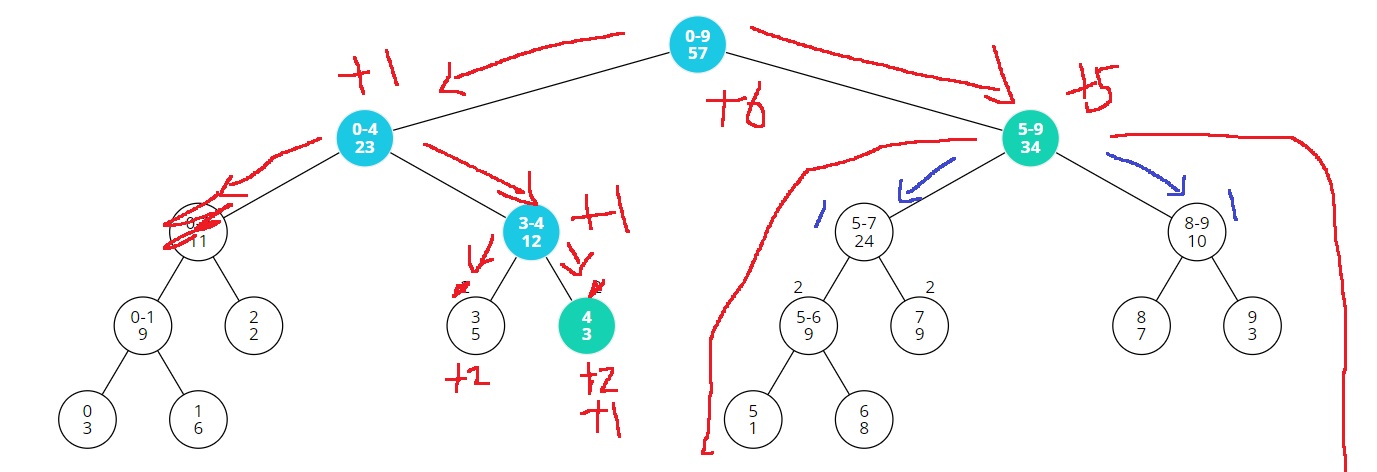
루트노드부터 탐색해서, 변경해야하는 값들을 저장하는 노드들은..
우리는 각 노드를 방문할때, 리프노드가 아니라면, 항상 두 자식 2*tree_index, 2*tree_index+1을 모두 호출해준다.
왜냐하면 두 자식에 lazy값이 저장되어 있을 수 있기 때문이다.
위 그림에서 [0,4]를 방문할때, [0,2]와 [3,4]를 모두 방문하는데, [0,2]에는 lazy가 0이기도 하고, [4,9]에 완전히 벗어나있으니 변경시키는 값은 없다.
[3,4]는 lazy가 0이지만, [4,9]에 일부 포함되어 있으므로 변경시켜야 하는 값이 존재한다.
[4,9]의 4가 포함되어 있으니 1을 더해주고, 두 자식 [3,3]과 [4,4]를 모두 호출해준다.

이제 [3,3]과 [4,4]를 방문했을때는, lazy값이 2로 존재하므로, lazy값을 더해서 갱신시켜준 다음에,
[3,3]은 [4,9]에 포함되어 있지 않으므로 1을 더하지 않고,
[4,4]는 [4,9]에 포함되어 있으므로 1을 더해준다.
그러니까 [3,3]에는 7이 저장되고, [4,4]에는 3+2+1=6이 저장된다.

여기서 왜 "느리게 갱신되는" 세그먼트 트리인지 알 수 있다.
이전에 [3,7]에 2를 더하고자 트리에 값을 변경시켰는데, 일부 갱신되지 않은 노드들은
추후에 다른 변경 연산, 그러니까 [4,9]에 1을 더하는 연산때 갱신되니까 "느리게 갱신되는" 세그먼트 트리라고 부른다.
다음 오른쪽 노드로 이동할때, [5,9]도 [4,9]에 포함되는 노드로, 5,6,7,8,9 5개가 있고, lazy는 0이니까.. 5를 더해준다

[3,7]에 2를 더할때 말한 것처럼, 초록색으로 표시된 노드들은 특별한 노드인데
그러니까 [left,right]에 완전히 [start,end]가 포함된 노드들은, 그 아래에 있는 자식 노드들도, 변경시켜야 하는 노드들인데,
바로 변경시키지 않고 lazy에 값을 저장해둔다음에, 나중에 변경시킨다고 말했다.
그러니까 [5,9]에 5를 더해준다음에, [5,7]과 [8,9]의 lazy에는 1을 저장해서 나중에 갱신시키기로 한다.
그래서 [4,9]에 1을 더하는 작업을 수행하면 세그먼트 트리는 다음과 같이 바뀐다.

이제 [6,8]에 존재하는 수들의 합을 구해본다면?
먼저 루트 노드 [0,9]는 [6,8]을 포함하므로, 왼쪽 자식, 오른쪽 자식으로 나누어 들어간다.
그런데, 왼쪽 자식 [0,4]는 [6,8]과 완전히 벗어나있으므로, 0을 return한다.

다음, [5,9]는 [6,8]을 포함하므로, 왼쪽, 오른쪽으로 나누어 들어가는데,
[5,7]로 들어갈때, lazy에 1이 저장되어 있다.
"앞으로 노드를 방문할 때, lazy에 값이 있는지 체크합니다.
lazy가 0이 아니라면, lazy에 들어간 값 * 구간에 들어간 원소의 수 = lazy[tree_index] * (end-start+1) 만큼 더해서 변경시켜주고,
lazy[tree_index] 값을 자식 노드에 넘겨줍니다."
그러므로 [5,7]에 1 * (7-5+1) = 3을 더해주고, 1을 두 자식 노드 [5,6]과 [7,7]에 넘겨준다.
그런데 [5,6]과 [7,7]에는 이미 lazy값이 2로 저장되어 있다.
1로 덮어씌우는가? 1을 더해주는가? 1을 더해주는게 맞다.
그러니까 lazy가 3으로 바뀐다.
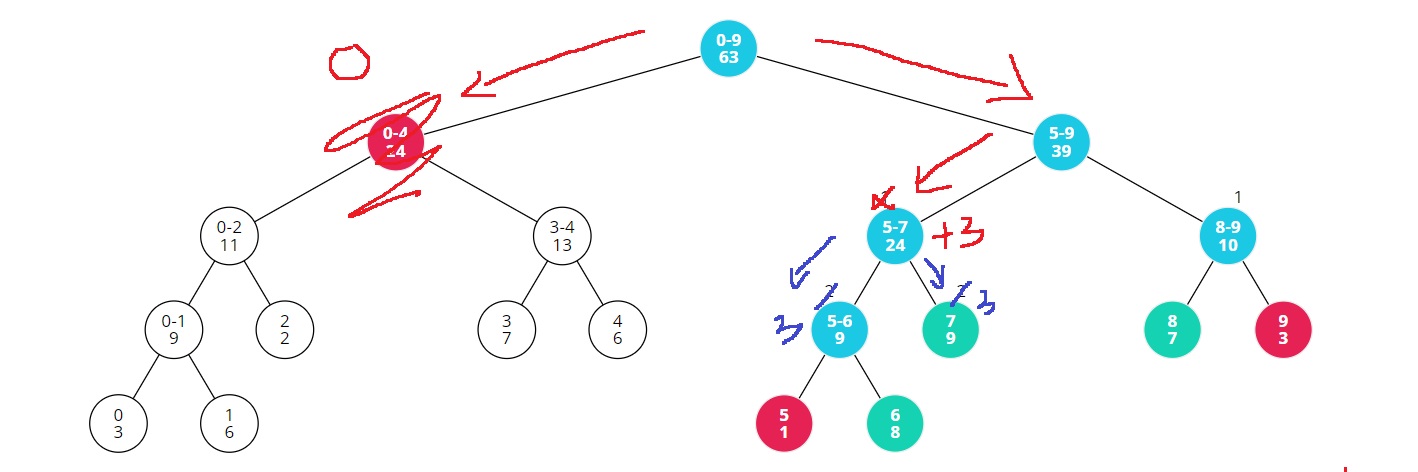
다시 [5,6]에는 lazy값이 존재한다.
그러므로 lazy * (end-start+1) = 3*(6-5+1) = 6을 더해주고, 두 자식 노드인 [5,5]와 [6,6]에 lazy값 3을 넘겨준다.
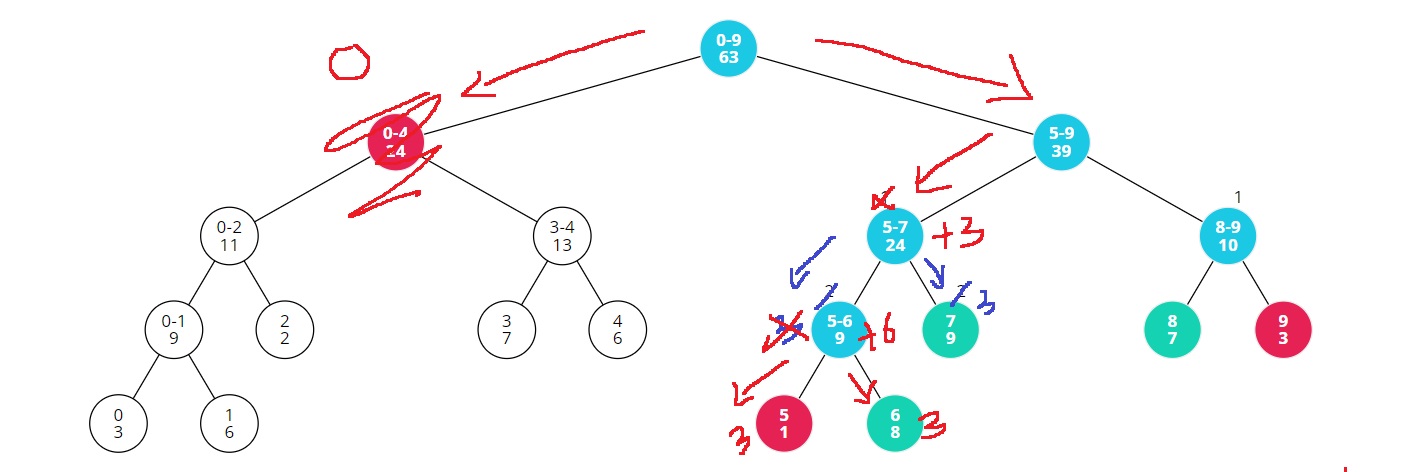
다음 [5,5]에는 lazy가 존재하니까, lazy를 더해서 저장된 값을 변경시켜준다.
그런데 [5,5]는 [6,8]에 벗어나므로 0을 return한다.
다음 오른쪽 [6,6]에는 lazy가 존재하므로 lazy를 더해서 저장된 값을 변경시켜준다.
그리고 [6,6]은 [6,8]에 완전히 포함되므로, 8+3=11을 return한다.
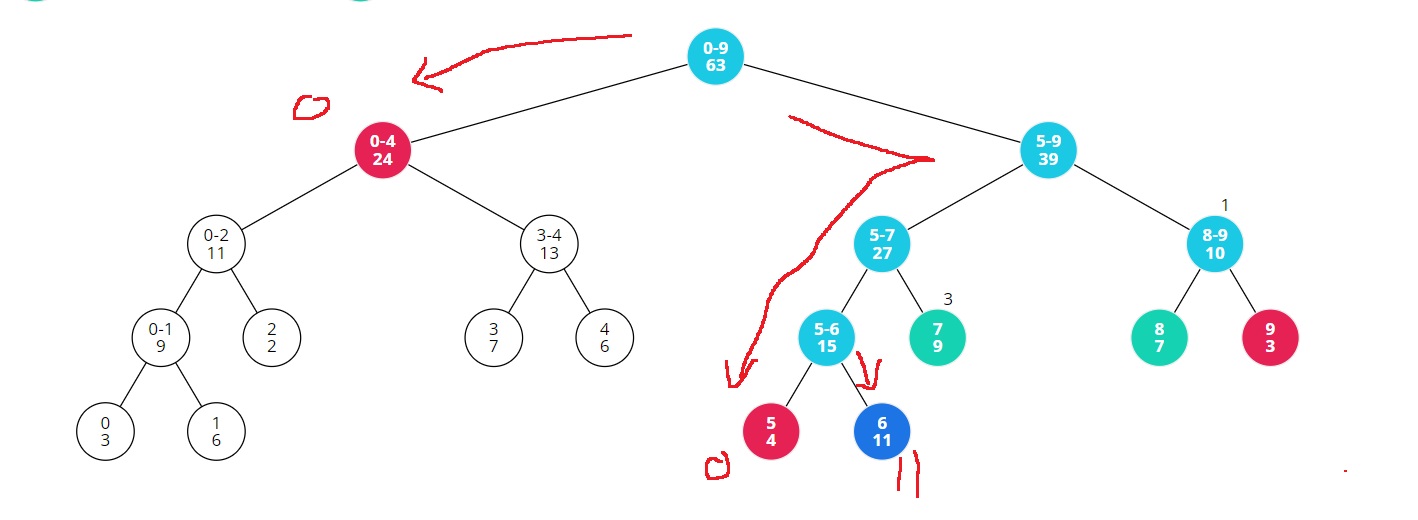
다시, [7,7]쪽으로 탐색을 진행하는데, lazy가 존재하므로, lazy를 더해서 저장된 값을 변경시킨다.
[7,7]은 [6,8]에 완전히 포함되므로, 9+3=12를 return한다.

다음에는, [8,9]를 방문하는데 lazy가 1로 존재하므로 lazy*(end-start+1) = 1*(9-8+1) = 2를 저장된 값에 더해서 변경시켜주고,
lazy값을 자식 노드 [8,8]과 [9,9]에 넘겨준다.

다시 [8,8]을 방문하면, lazy값이 1로 존재하므로 lazy를 더해줘서 값을 변경시키고
[8,8]은 [6,8]에 완전히 포함되므로 8을 return한다.
오른쪽 [9,9]를 방문하면, lazy값이 1로 존재하므로 lazy를 더해서 값을 변경시키나, [9,9]는 [6,8]에 벗어나므로 0을 return한다.

그래서 [6,8]의 합을 구하면, 31이 된다.
그리고 "느리게 갱신된" 세그먼트 트리는 다음과 같이 바뀐다.
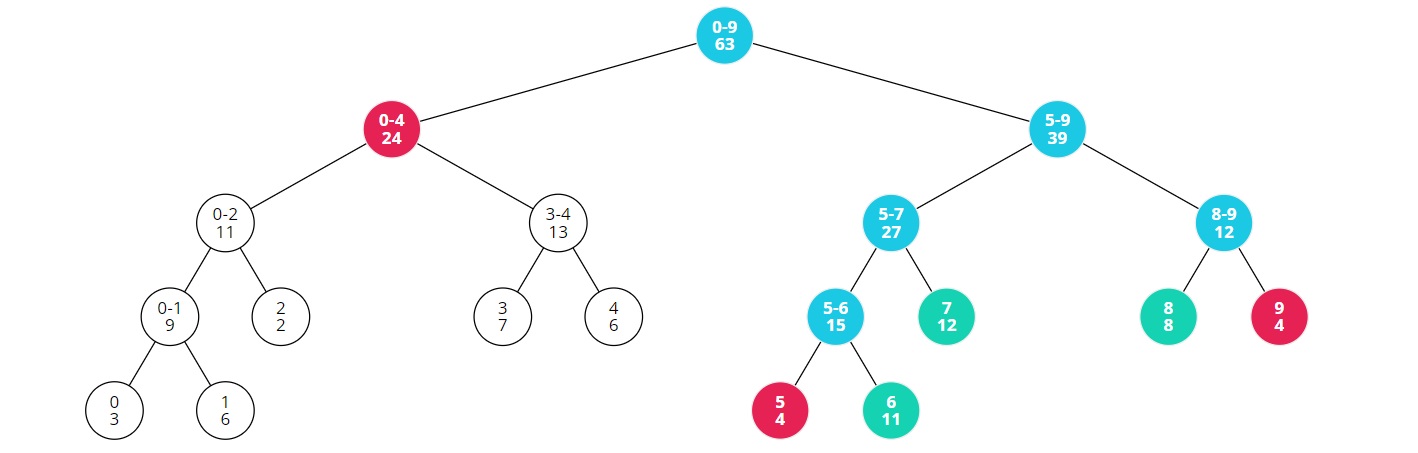
이렇게 하면 합을 구할때 방문하는 노드와 수를 변경할때 방문하는 노드가 동일해져서
합을 구하는 연산과 변경하는 연산이 O(logN)이 된다
4. 구현 예시 - 느리게 갱신되는 세그먼트 트리
편의상 구간의 합을 구하는 세그먼트 트리를 만들어보자.
먼저 세그먼트 트리를 만드는 함수는 이전과 동일하다
def create_segment(A,tree,tree_index,A_start,A_end):
if A_start == A_end:
tree[tree_index] = A[A_start]
else:
A_mid = (A_start+A_end)//2
create_segment(A,tree,2*tree_index,A_start,A_mid)
create_segment(A,tree,2*tree_index+1,A_mid+1,A_end)
tree[tree_index] = tree[2*tree_index] + tree[2*tree_index+1]
다음으로 구간에 어떤 수 value를 더하는 함수를 생각해보자.
[left,right]에 value를 더한다고 할때, 특정 구간에 저장된 구간이 [start,end]라고 한다면...
[start,end]와 [left,right]가 완전히 벗어나면 아무것도 하지 않고 return
def update_range(tree,lazy,tree_index,start,end,left,right,value):
if left > end or right < start:
return
다음, [left,right]안에 [start,end]가 완전히 포함된 경우, 이들은 값을 변경시켜야 하는 대상이다.
그러니까 [start,end]의 모든 수들에 value를 더해줘야한다.
[start,end]에 들어간 원소의 개수는 (end-start+1)이므로, tree[tree_index]에 (end-start+1) * value를 더해준다.
def update_range(tree,lazy,tree_index,start,end,left,right,value):
if left > end or right < start:
return
if left <= start and end <= right:
tree[tree_index] += (end-start+1)*value
이거는 어떤 과정들이 지금 된걸까?
위에서 예시를 들때, [3,7]에 2를 더하는 과정에서..

초록색 노드들이 [left,right]안에 [start,end]가 완전히 포함된 경우이다..
이 경우 만약 리프노드가 아니라면, 두 자식 노드에 lazy값을 저장한다고 했다.
리프노드가 아닌 것은 start != end인 경우이다.
start != end인 경우, 두 자식 노드 2*tree_index와 2*tree_index+1의 lazy값에 value를 저장시켜준다.
def update_range(tree,lazy,tree_index,start,end,left,right,value):
#[left,right]와 [start,end]가 완전히 벗어나는 경우
#그냥 return하고 탐색 종료
if left > end or right < start:
return
#[left,right]안에 [start,end]가 완전히 포함된 경우
if left <= start and end <= right:
#[start,end]안에 포함된 수들에 value를 모두 더해준다.
#[start,end]안에 포함된 수들의 개수는 (end-start+1)개
tree[tree_index] += (end-start+1)*value
#그런데 start != end인 경우, 리프노드가 아닌 경우에는..
#두 자식 노드 2*tree_index, 2*tree_index+1의 lazy배열에 value를 더해준다.
if start != end:
lazy[2*tree_index] += value
lazy[2*tree_index+1] += value
return #더 이상 아래로 내려가지 않는다.
[5,7]에 도달할때, 값을 변경시켜주고 두 자식 노드에 lazy를 저장한다음에,
[5,6]아래의 자식 [5,5]와 [6,6]에는 lazy값에 저장하지 않는다...
그러니까 바로 아래 자식에만 lazy 값을 저장시켜주고, return해서 탐색 종료시키기
그런데...
왜 lazy[2*tree_index] = value가 아니고 lazy[2*tree_index] += value야???
그것은 당연히, 구간을 변경시키는 쿼리를 연속해서 하는 경우, 누적 시켜서 나중에 해당 노드를 방문할때, 한번에 변경시킬거니까..
그러니까 심플하게 [3,7]에 2를 더하는 쿼리를 수행하고,

다시 [3,7]에 3을 더하는 쿼리를 수행하면..?
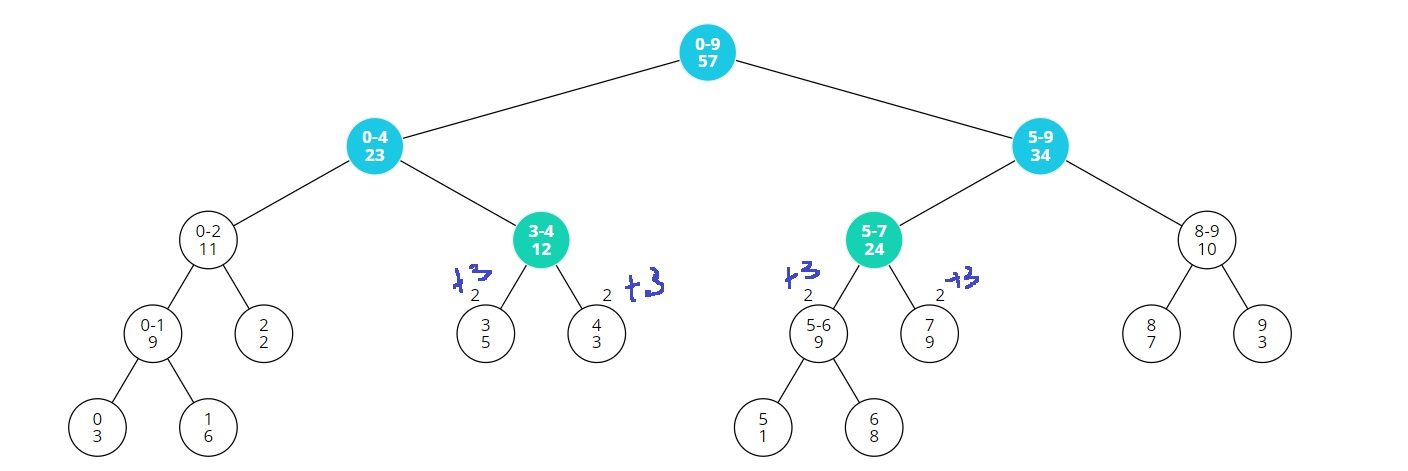
아직 [3,3], [4,4], [5,6], [7,7]을 방문하지 않았으니까, lazy는 사용되는게 아니고 누적시켜놔야겠지..
나중에 "방문하면" lazy를 사용해서 갱신시킬거니까
아무튼... 1) [left,right]와 [start,end]가 완전히 벗어나있는경우<빨간색>, 2) [left,right] 안에 [start,end]가 완전히 포함된 경우 <초록색>
는 처리했다.
그러면 그 이외의 경우, [left,right]와 [start,end]가 일부만 겹치는 경우<파란색>를 처리해야겠지?
그거는 왼쪽, 오른쪽으로 나누어 탐색에 들어가고, 위 2가지 경우에서 return되면서, 변경된 값들을 이용해서 변경시키는 작업을 수행해야겠지
def update_range(tree,lazy,tree_index,start,end,left,right,value):
#<빨간색>부분
#[left,right]와 [start,end]가 완전히 벗어나는 경우
#그냥 return하고 탐색 종료
if left > end or right < start:
return
#<초록색>부분
#[left,right]안에 [start,end]가 완전히 포함된 경우
if left <= start and end <= right:
#[start,end]안에 포함된 수들에 value를 모두 더해준다.
#[start,end]안에 포함된 수들의 개수는 (end-start+1)개
tree[tree_index] += (end-start+1)*value
#그런데 start != end인 경우, 리프노드가 아닌 경우에는..
#두 자식 노드 2*tree_index, 2*tree_index+1의 lazy배열에 value를 더해준다.
if start != end:
lazy[2*tree_index] += value
lazy[2*tree_index+1] += value
return #더 이상 아래로 내려가지 않는다.
#<파란색>부분
#[left,right]와 [start,end]가 일부만 겹치는 경우
#왼쪽, 오른쪽으로 나누어 탐색
mid = (start+end)//2
update_range(tree,lazy,2*tree_index,start,mid,left,right,value)
update_range(tree,lazy,2*tree_index+1,mid+1,end,left,right,value)
#위의 <빨간색>, <초록색>에서 return되면서 변경된 자식값들을 가지고와, 올라오면서,
#값들을 변경해주는 작업
tree[tree_index] = tree[2*tree_index] + tree[2*tree_index+1]
구간의 합을 구하는 함수는 변경된 것이 없었다.. 이전과 동일하다
#구간 [left,right]의 합을 구하는 함수
def query_sum(tree,tree_index,start,end,left,right):
#[left,right]가 [start,end]와 완전히 벗어난 경우
if left > end or right < start:
return 0
#[left,right]안에 [start,end]가 완전히 포함된 경우
if left <= start and end <= right:
return tree[tree_index]
#[left,right]와 [start,end]가 일부만 겹치는 경우
#왼쪽, 오른쪽 나누어 탐색
mid = (start+end)//2
left_sum = query_sum(tree,2*tree_index,start,mid,left,right)
right_sum = query_sum(tree,2*tree_index+1,mid+1,end,left,right)
return left_sum + right_sum
그런데... 하나 놓친게 있다.
"앞으로 노드를 방문할 때, lazy에 값이 있는지 체크합니다.
lazy가 0이 아니라면, lazy에 들어간 값 * 구간에 들어간 원소의 수 = lazy[tree_index] * (end-start+1) 만큼 더해서 변경시켜주고,
lazy[tree_index] 값을 자식 노드에 넘겨줍니다."
lazy를 체크하고, lazy가 존재하면 lazy값을 더해서 값을 변경시켜준 다음에, 자식 노드에 lazy값을 넘겨주는 작업을 수행하지 않았음
그것을 수행하는 함수를 작성하자
방문하는 노드의 인덱스인 tree_index에 lazy값이 0이 아니라면...
해당 노드에 저장된 값에, lazy[tree_index]값을 더해준다.
그런데, 해당 노드가 [start,end]를 저장하는 구간이라면, [start,end]에 포함된 모든 수들에 lazy[tree_index]를 더해준다.
[start,end]에 포함된 수들은 모두 (end-start+1)개이다.
따라서, tree[tree_index]에 (end-start+1)*lazy[tree_index]를 더해준다.
#lazy배열을 업데이트 하는 함수
#[start,end]는 방문한 노드가 저장하는 구간
def update_lazy(tree,lazy,tree_index,start,end):
#방문한 노드에 저장된 lazy가 0이 아니라면..
if lazy[tree_index] != 0:
#해당 노드가 저장하는 구간 [start,end]에 포함된 모든 수들에 lazy[tree_index]를 더해준다.
#[start,end]에 포함된 모든 수들의 개수는 (end-start+1)
#따라서, tree[tree_index]에 (end-start+1)*lazy[tree-index]를 더해준다.
tree[tree_index] += (end-start+1)*lazy[tree_index]
다음, 해당 lazy를 변경시키고 나서 자식 노드에 lazy값을 전달시키는 작업이 필요하다.
해당 노드가 리프노드가 아니라면, 즉, start != end라면, 두 자식 노드 2*tree_index, 2*tree_index+1에 lazy[tree_index]를 전달해준다.
전달해줄때는 원래 있던 lazy값에 누적합을 시켜줘야한다는 것은...

여기서 했었어.. 원래 2가 있었는데, 1을 전달해주면 3이 된다는거..
#lazy배열을 업데이트 하는 함수
#[start,end]는 방문한 노드가 저장하는 구간
def update_lazy(tree,lazy,tree_index,start,end):
#방문한 노드에 저장된 lazy가 0이 아니라면..
if lazy[tree_index] != 0:
#해당 노드가 저장하는 구간 [start,end]에 포함된 모든 수들에 lazy[tree_index]를 더해준다.
#[start,end]에 포함된 모든 수들의 개수는 (end-start+1)
#따라서, tree[tree_index]에 (end-start+1)*lazy[tree-index]를 더해준다.
tree[tree_index] += (end-start+1)*lazy[tree_index]
#만약 리프노드가 아니라면..
if start != end:
#두 자식노드에 lazy값을 전달해준다
lazy[2*tree_index] += lazy[tree_index]
lazy[2*tree_index+1] += lazy[tree_index]
그리고 lazy를 사용해서 변경시켜주면, 현재 저장된 lazy값은 없애준다는 것은... 예시를 들면서 (따로 말은 안했지만) 이미 보였다고 생각한다
#lazy배열을 업데이트 하는 함수
#[start,end]는 방문한 노드가 저장하는 구간
def update_lazy(tree,lazy,tree_index,start,end):
#방문한 노드에 저장된 lazy가 0이 아니라면..
if lazy[tree_index] != 0:
#해당 노드가 저장하는 구간 [start,end]에 포함된 모든 수들에 lazy[tree_index]를 더해준다.
#[start,end]에 포함된 모든 수들의 개수는 (end-start+1)
#따라서, tree[tree_index]에 (end-start+1)*lazy[tree-index]를 더해준다.
tree[tree_index] += (end-start+1)*lazy[tree_index]
#만약 리프노드가 아니라면..
if start != end:
#두 자식노드에 lazy값을 전달해준다
lazy[2*tree_index] += lazy[tree_index]
lazy[2*tree_index+1] += lazy[tree_index]
#변경에 사용한 lazy값은 초기화시킨다.
lazy[tree_index] = 0
위 함수는 특정 노드를 방문할때 수행하는 lazy를 업데이트 하는 함수이고, 특정 노드를 방문하는 작업은
구간 합을 구하는 쿼리나, 구간을 변경시키는 쿼리를 수행할때 모두 이루어지는 작업이다.
그래서 구간 합을 구하는 함수와 구간을 변경시키는 함수에 lazy 배열을 업데이트 하는 함수를 추가해줘야한다.
그러니까, update_lazy()는 세그먼트 트리를 "느리게 갱신시키는"함수이다.
구간을 변경시키는 update_range()함수 수행할때, 맨 처음에 update_lazy()함수를 수행해준다..
def update_range(tree,lazy,tree_index,start,end,left,right,value):
#노드를 방문하면서, lazy값이 존재하는지 확인하면서 트리를 갱신시킨다.
#그러니까 lazy 배열을 업데이트한다.
update_lazy(tree,lazy,tree_index,start,end)
#<빨간색>부분
#[left,right]와 [start,end]가 완전히 벗어나는 경우
#그냥 return하고 탐색 종료
if left > end or right < start:
return
#<초록색>부분
#[left,right]안에 [start,end]가 완전히 포함된 경우
if left <= start and end <= right:
#[start,end]안에 포함된 수들에 value를 모두 더해준다.
#[start,end]안에 포함된 수들의 개수는 (end-start+1)개
tree[tree_index] += (end-start+1)*value
#그런데 start != end인 경우, 리프노드가 아닌 경우에는..
#두 자식 노드 2*tree_index, 2*tree_index+1의 lazy배열에 value를 더해준다.
if start != end:
lazy[2*tree_index] += value
lazy[2*tree_index+1] += value
return #더 이상 아래로 내려가지 않는다.
#<파란색>부분
#[left,right]와 [start,end]가 일부만 겹치는 경우
#왼쪽, 오른쪽으로 나누어 탐색
mid = (start+end)//2
update_range(tree,lazy,2*tree_index,start,mid,left,right,value)
update_range(tree,lazy,2*tree_index+1,mid+1,end,left,right,value)
#위의 <빨간색>, <초록색>에서 return되면서 변경된 자식값들을 가지고와, 올라오면서,
#값들을 변경해주는 작업
tree[tree_index] = tree[2*tree_index] + tree[2*tree_index+1]
역시 구간 합을 구하는 함수 query_sum()의 맨 처음에 lazy배열을 업데이트 하는 함수 update_lazy()를 수행해준다.
#구간 [left,right]의 합을 구하는 함수
def query_sum(tree,lazy,tree_index,start,end,left,right):
#노드를 방문하면서, lazy값이 존재하는지 확인하면서 트리를 갱신시킨다.
#그러니까 lazy 배열을 업데이트한다.
update_lazy(tree,lazy,tree_index,start,end)
#[left,right]가 [start,end]와 완전히 벗어난 경우
if left > end or right < start:
return 0
#[left,right]안에 [start,end]가 완전히 포함된 경우
if left <= start and end <= right:
return tree[tree_index]
#[left,right]와 [start,end]가 일부만 겹치는 경우
#왼쪽, 오른쪽 나누어 탐색
mid = (start+end)//2
left_sum = query_sum(tree,lazy,2*tree_index,start,mid,left,right)
right_sum = query_sum(tree,lazy,2*tree_index+1,mid+1,end,left,right)
return left_sum + right_sum
lazy 배열은 크기를 어떻게 만들어줘야할까?
세그먼트 트리의 각 노드에 저장되는 값이므로, 당연히 세그먼트 트리의 크기와 동일하게 만들면 되겠다.
따라서 최종 "느리게 갱신되는" 세그먼트 트리는..
import math
#세그먼트 트리를 생성하는 함수
def create_segment(A,tree,tree_index,A_start,A_end):
if A_start == A_end:
tree[tree_index] = A[A_start]
else:
A_mid = (A_start+A_end)//2
create_segment(A,tree,2*tree_index,A_start,A_mid)
create_segment(A,tree,2*tree_index+1,A_mid+1,A_end)
tree[tree_index] = tree[2*tree_index] + tree[2*tree_index+1]
#lazy배열을 업데이트 하는 함수
#[start,end]는 방문한 노드가 저장하는 구간
def update_lazy(tree,lazy,tree_index,start,end):
#방문한 노드에 저장된 lazy가 0이 아니라면..
if lazy[tree_index] != 0:
#해당 노드가 저장하는 구간 [start,end]에 포함된 모든 수들에 lazy[tree_index]를 더해준다.
#[start,end]에 포함된 모든 수들의 개수는 (end-start+1)
#따라서, tree[tree_index]에 (end-start+1)*lazy[tree-index]를 더해준다.
tree[tree_index] += (end-start+1)*lazy[tree_index]
#만약 리프노드가 아니라면..
if start != end:
#두 자식노드에 lazy값을 전달해준다
lazy[2*tree_index] += lazy[tree_index]
lazy[2*tree_index+1] += lazy[tree_index]
#변경에 사용한 lazy값은 초기화시킨다.
lazy[tree_index] = 0
#구간 [left,right]의 모든 원소에 value를 더해주는 함수
def update_range(tree,lazy,tree_index,start,end,left,right,value):
#노드를 방문하면서, lazy값이 존재하는지 확인하면서 트리를 갱신시킨다.
#그러니까 lazy 배열을 업데이트한다.
update_lazy(tree,lazy,tree_index,start,end)
#<빨간색>부분
#[left,right]와 [start,end]가 완전히 벗어나는 경우
#그냥 return하고 탐색 종료
if left > end or right < start:
return
#<초록색>부분
#[left,right]안에 [start,end]가 완전히 포함된 경우
if left <= start and end <= right:
#[start,end]안에 포함된 수들에 value를 모두 더해준다.
#[start,end]안에 포함된 수들의 개수는 (end-start+1)개
tree[tree_index] += (end-start+1)*value
#그런데 start != end인 경우, 리프노드가 아닌 경우에는..
#두 자식 노드 2*tree_index, 2*tree_index+1의 lazy배열에 value를 더해준다.
if start != end:
lazy[2*tree_index] += value
lazy[2*tree_index+1] += value
return #더 이상 아래로 내려가지 않는다.
#<파란색>부분
#[left,right]와 [start,end]가 일부만 겹치는 경우
#왼쪽, 오른쪽으로 나누어 탐색
mid = (start+end)//2
update_range(tree,lazy,2*tree_index,start,mid,left,right,value)
update_range(tree,lazy,2*tree_index+1,mid+1,end,left,right,value)
#위의 <빨간색>, <초록색>에서 return되면서 변경된 자식값들을 가지고와, 올라오면서,
#값들을 변경해주는 작업
tree[tree_index] = tree[2*tree_index] + tree[2*tree_index+1]
#구간 [left,right]의 합을 구하는 함수
def query_sum(tree,lazy,tree_index,start,end,left,right):
#노드를 방문하면서, lazy값이 존재하는지 확인하면서 트리를 갱신시킨다.
#그러니까 lazy 배열을 업데이트한다.
update_lazy(tree,lazy,tree_index,start,end)
#[left,right]가 [start,end]와 완전히 벗어난 경우
if left > end or right < start:
return 0
#[left,right]안에 [start,end]가 완전히 포함된 경우
if left <= start and end <= right:
return tree[tree_index]
#[left,right]와 [start,end]가 일부만 겹치는 경우
#왼쪽, 오른쪽 나누어 탐색
mid = (start+end)//2
left_sum = query_sum(tree,lazy,2*tree_index,start,mid,left,right)
right_sum = query_sum(tree,lazy,2*tree_index+1,mid+1,end,left,right)
return left_sum + right_sum
#입력
A = [1,2,3,4,5,6,7,8,9,10] #주어진 정수 배열
N = 10 #배열 A의 크기
n = 2**(math.ceil(math.log2(N))+1)-1 #세그먼트 트리의 크기
#세그먼트 트리 초기화
tree = [0] * (n+1)
#lazy배열 초기화
lazy = [0] * (n+1)
참조
느리게 갱신되는 세그먼트 트리 (acmicpc.net)
느리게 갱신되는 세그먼트 트리
소스 1void update_range(vector &tree, int node, int start, int end, int left, int right, long long diff) { if (left > end || right < start) { return; } if (start == end) { tree[node] += diff; return; } update_range(tree, node*2, start, (start+end)/2, lef
book.acmicpc.net
'알고리즘 > 세그먼트 트리' 카테고리의 다른 글
| 세그먼트 트리 응용 - XOR 연산을 수행하는 트리 (0) | 2022.12.15 |
|---|---|
| 느리게 갱신되는 세그먼트 트리 응용 -리프노드의 값을 출력하는 트리?- (0) | 2022.12.13 |
| 파이썬 알고리즘 기본기 곱셈 연산에서 주의할 점 배우기(세그먼트 트리 문제) (0) | 2022.12.10 |
| 세그먼트 트리 응용2 -최솟값과 최댓값을 구하는 세그먼트 트리- (0) | 2022.12.08 |
| 세그먼트 트리 응용1 - 구간의 곱을 구하는 세그먼트 트리 (0) | 2022.12.06 |

