1. 문제
22964번: conv1d
A = [1, 1], B = [1] : 1 1 A = [1, 1], B = [2] : 2 2 A = [1, 2], B = [1] : 1 2 A = [1, 2], B = [2] : 2 4 A = [2, 1], B = [1] : 2 1 A = [2, 1], B = [2] : 4 2 A = [2, 2], B = [1] : 2 2 A = [2, 2], B = [2] : 4 4 1+2+1+2+2+4+2+4 = 18 1+2+2+4+1+2+2+4 = 18
www.acmicpc.net
입력데이터와 필터가 주어질때, 1차원 convolution 연산을 수행하는 문제
2. 풀이
역시 만만한 문제가 아니다
단순히 곱하는거면 문제가 아닌데,
입력데이터와 필터의 최대 20만개의 원소가 1부터 20만까지 될 수 있을때, 이러한 모든 조합의 가능한 경우를 모두 구해야하는데
이게 2초만에 가능한가??
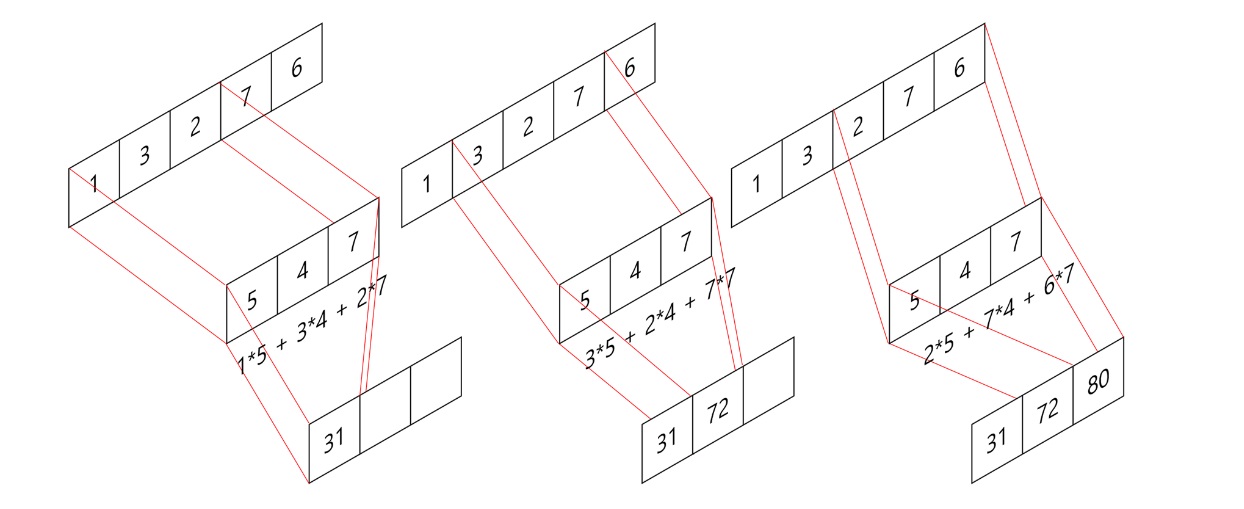
저번에 perceptron 계산할때처럼 임의의 값으로 미리 한번 계산해보자
만약 입력이 [a,b]이고 필터가 [k]라고 한다면...?
그러면 결과는 [ak, bk]가 될거다.
이제 a,b,k는 1이상 x이하의 정수인데, 이러한 모든 경우에 대하여 ak의 합과 bk의 합을 각각 출력하는게 문제다.
그러니까 문제는
$$[\sum_{a=1}^{x}\sum_{k=1}^{x}ak, \sum_{b=1}^{x}\sum_{k=1}^{x}bk]$$
를 출력하면 된다
그러면 이제 문제는.. $\sum_{a=1}^{x}\sum_{k=1}^{x}ak$ 이걸 어떻게 구할 수 있을까?
아주 간단하다.. 시그마에 영향받지 않은 항은 상수로 취급해서 뺄 수 있으므로..
$$\sum_{a=1}^{x}\sum_{k=1}^{x}ak = \sum_{a=1}^{x} a \sum_{k=1}^{x} k = (\frac{x(x+1)}{2})^{2}$$
------------------------------------------------------------------------------------------------------------------------------------------
다음으로.. 항 수를 늘려서 생각해보자.
만약 입력데이터가 [a,b,c,d]이고 필터가 [y,z]라고 한다면?
결과는 [ay+bz, by+cz, cy+dz]
그러면 필터가 [y,z,w]라고 한다면?
결과는 [ay+bz+cw, by+cz+dw]
....
만약 입력데이터가 $[a_{1}, a_{2}, a_{3}, ... , a_{n}]$이고 필터가 $[b_{1}, b_{2}, ... , b_{k}]$라고 하자.
그러면 convolution 결과는..
첫번째 원소는.. $a_{1}b_{1} + a_{2}b_{2} + ... + a_{k}b_{k}$
두번째 원소는.. $a_{2}b_{1} + a_{3}b_{2} + ... + a_{k+1}b_{k}$
...
이것이 몇개가 있나?? 문제에서 친절하게 n-k+1개가 있다고도 알려준다
n-k+1번째 원소는.. $a_{n-k+1}b_{1} + a_{n-k+2}b_{2} + ... + a_{n}b_{k}$
그러면 각각의 원소가 몇개의 항의 합으로 이루어져 있는가?
$a_{1}b_{1} + a_{2}b_{2} + ... + a_{k}b_{k}$ 봐도 알 수 있잖아.. k개의 항의 합으로 이루어져 있지
그런데 각 항은?
위에서 구한 $\sum_{a=1}^{x}\sum_{k=1}^{x}ak$의 형태이다.
그러므로 우리는 임의의 i번째 원소는... $\sum_{n=1}^{k}\sum_{a=1}^{x}\sum_{b=1}^{x}ab$로 나타낼 수 있다.
이걸 계산하면?
$$\sum_{n=1}^{k}\sum_{a=1}^{x}\sum_{b=1}^{x}ab = k(\frac{x(x+1)}{2})^{2}$$
그런데 모든 i번째 원소가 동일하므로 $k(\frac{x(x+1)}{2})^{2}$를 n-k+1개 출력하면 된다
---------------------------------------------------------------------------------------------------------------------------------------------------
그런데 마지막으로 문제는...
문제 예시에서 n=2, k=1, x=2에서
각 원소가 1이상 2이하일때, 가능한 경우의 수로

이렇게 힌트를 주고 있는데.. 내가 구한대로 구하면 $k(\frac{x(x+1)}{2})^{2} = 9$가 나오거든?
왜 그런지 생각해보면..

a=1이고 k=1인 경우가 몇가지가 되는지를 생각해보면..
b=1이고 b=2더라도 서로 다른경우라는거지

하지만 내가 계산할때는, ak의 합에서 b는 고려하지 않고 계산해서... 결과가 조금 다르다
그러면 이 경우의 수를 어떻게 알 수 있을까?
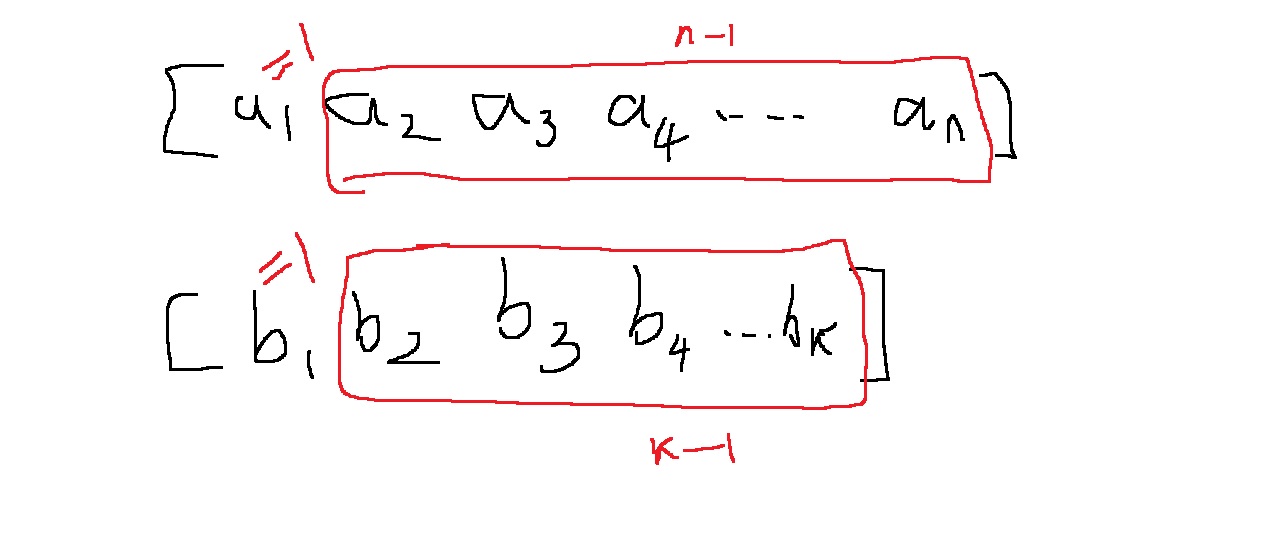
입력데이터 n개와 필터 k개를 그림으로 그려서 생각해보면 간단하다.
$a_{1}$와 $b_{1}$가 어떤 수로 고정되어 있다고 생각하면...
$a_{2}$부터 $a_{n}$까지를 결정하는 방법의 수는 몇가지인가?
각각은 1이상 x이하의 정수이고 전부 n-1개이므로 $x^{n-1}$가지가 된다
마찬가지로 $b_{2}$부터 $b_{k}$까지를 결정하는 방법의 수는?
각각은 1이상 x이하의 정수이고 전부 k-1개이므로 $x^{k-1}$가지이다.

이것이 무슨 뜻일까?
$a_{1}$와 $b_{1}$이 각각 어떤 수 a,b로 고정되어 있을때, 각각은 모두 가능한 경우의 수가 $x^{n-1} x^{k-1}$가지라는 뜻이다.
그러므로, convolution 결과의 첫번째 원소가 나올 수 있는 모든 가능한 경우의 총 합은...
$k(\frac{x(x+1)}{2})^{2}$가 총 $x^{n-1} x^{k-1}$가지가 가능하므로...
$$x^{n-1}x^{k-1}k(\frac{x(x+1)}{2})^{2}$$
이것은 모든 n-k+1개의 모든 임의의 원소에 해당되는 사실임을 위에서 이미 보였다.
3. 구현
이제 문제는 아주 간단해졌다
$$x^{n-1}x^{k-1}k(\frac{x(x+1)}{2})^{2}$$을 n-k+1개 한줄로 출력하면 끝이다.
그런데 여기서도 문제에 나와있듯이
결과가 아주 커질 수 있으므로 998244353으로 나눈 나머지를 구하라고 한다
x가 20만이고 n이 20만, k가 20만까지 가면 당장 $x^{n-1}$도 0.3초나 걸림
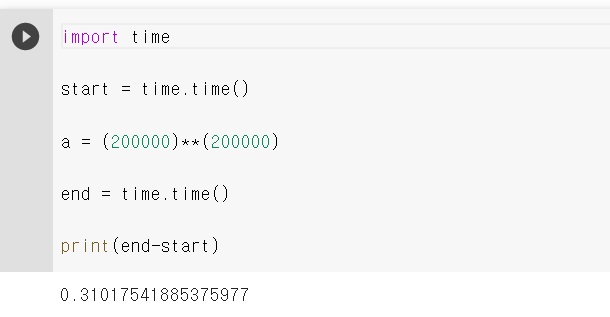
그냥 해도 사실 통과는 할 수 있는데.. 이제 조금 더 효율적으로 하고 싶으면
파이썬에서 pow함수를 제공하는데

pow(x,y,z)로 제공하면... x**y를 z로 나눈 나머지를 제공함
그런데 이는 pow(x,y) % z보다 더 효율적으로 계산해준다고 함
그리고 pow(x,y)는 x**y와 동일하다고도 나와 있음
그러니까 (x**y)%z보다 pow(x,y,z)하면 훨씬 빠르다는 뜻이겠지..
실제로 (x**y)%z로 제출하면 1초 걸리는데 pow(x,y,z)로 제출하면 0.1로 걸리더라
from sys import stdin
n,k,x = map(int,stdin.readline().split())
sum_ax = k*(pow(x*(x+1)//2,2,998244353))
case = (pow(x,n-1,998244353)*pow(x,k-1,998244353))
value = sum_ax*case%998244353
print(*([value]*(n-k+1)))
그리고 참고로 pow(x,n+k-2,998244353)보다 나눠서 pow(x,n-1,998244353) * pow(x,k-1,998244353)으로 구하는게 큰 차이는 없지만 조금 더 빠름..
거듭제곱의 분할정복과 비슷한 원리겠지?
+ 또 참고지만 리스트의 곱셈 연산이 for _ in range(n)보다 더 빠르다고는 함...
물론 곱셈 연산하면 얕은복사가 된다는 점은 주의해야지
파이썬 알고리즘 관련 시간을 줄이는 팁들 (tistory.com)
파이썬 알고리즘 관련 시간을 줄이는 팁들
자고로 시간을 줄이는 것은 언제나 알고리즘에 있어 지향해야할 목표점이다. 아직 알고리즘 초보라 편법처럼이라도 시간을 줄이고픈 마음에 팁들이 생길 때마다 추가하려고 한다. 입력 - sys 모
lgphone.tistory.com
'알고리즘 > 구현,시뮬레이션' 카테고리의 다른 글
| 문자열 정렬할 때 실수하기 쉬운부분 복기하기 -줄서기- (0) | 2023.01.29 |
|---|---|
| 인공신경망 Perceptron 효과적으로 출력값을 계산하는 방법은? (0) | 2022.12.09 |
| 프로그래밍으로 뱀을 만드는 방법? -뱀- (0) | 2022.11.13 |
| 주사위를 구현하는 방법 - 주사위 굴리기 - (0) | 2022.11.12 |
| 조금 더 어려운 시뮬레이션 연습하기 -미세먼지 안녕!- (0) | 2022.11.08 |

