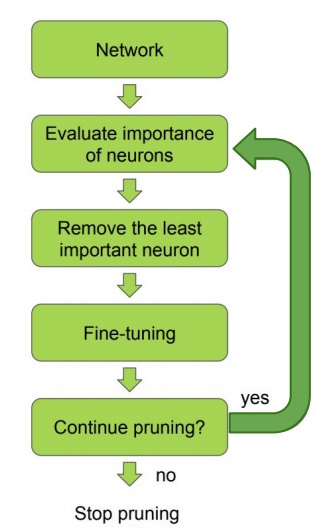
1. iterative pruning
network가 존재하면 neuron weight들의 중요도를 계산함
중요도가 적은 weight는 적절하게 제거함
이후 데이터를 다시 넣어 fine-tuning을 수행하면서 weight를 업데이트
pruning을 계속하고 싶으면 weight의 중요도를 다시 계산하여 위 과정을 반복
pruning을 중단하고 싶으면 그대로 사용.. 단 1번만 할 수는 있지만 보통 여러번 반복 pruning을 수행함
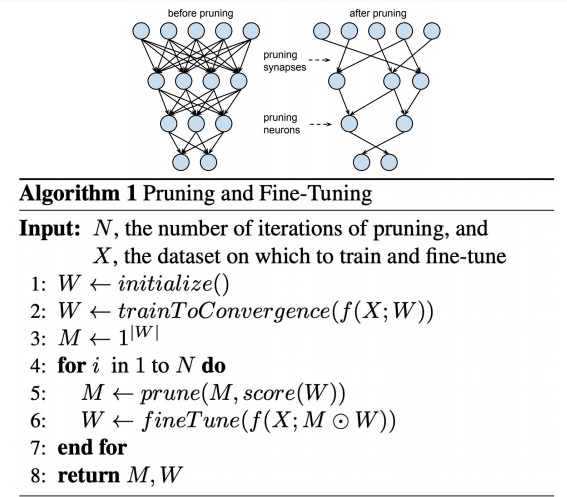
2. pruning의 알고리즘
N이 pruning의 반복수이고 X가 훈련데이터(fine-tuning에도 사용)
먼저 weight를 초기화하고 network를 training하여 weight를 convergence시킴
weight의 차원과 크기가 동일한 1로 가득찬 mask 행렬을 생성
pruning을 N번 반복수행을 하는데
Weight의 중요도를 계산하여 mask를 업데이트함
업데이트된 mask를 weight에 씌우면 그것이 1번의 pruning임
그리고 pruning된 weight를 가진 network에 대해 fine-tuning을 수행하여 weight를 다시 업데이트
N번 반복하면 mask M과 최종 업데이트된 weight를 얻을 것
3. dropout의 알고리즘
확률 p를 가지는 베르누이분포(이거는 근데 원하면 바꿀 수 있지는 않을까)에서 랜덤하게 난수를 생성
베르누이분포는 0 아니면 1을 뽑으니까 y에 곱해서 feedforward를 수행하면
0을 곱한경우는 weight가 꺼진거고 1을 곱한경우는 weight를 그대로 가지고 feedforward를 수행하는 것임

4. regularization에 따른 pruning
training시 L2 regularization을 수행하고 pruning을 하는 것과 L1 regularization을 수행하고 pruning을 수행하는 것에서 성능 손해가 전자가 더 심하다
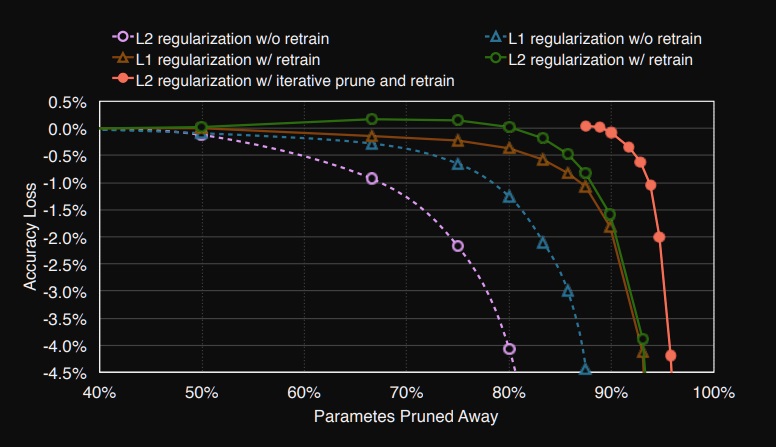
regularization에 따른 pruning시 정확도 손해 그림
위 그래프를 보면 보라색 선이 L2 regularization을 하면서 training할 때 pruning을 수행한 것이고
파란색 선이 L1 regularization을 하면서 pruning을 수행한 것
보면 동일한 양의 pruning을 수행했을때 L2 regularization이 정확도 손해가 심하다
왜냐하면 이전에 배운 것처럼 L1 regularization은 대부분의 parameter를 0으로 보내는 성질이 있어서
동일한 양의 pruning으로 parameter를 날려버릴때 L1 regularization의 경우가 0으로 된 parameter가 많아 필요없는 parameter가 제거될 가능성이 높으므로 정확도 손해가 별로없다.
그러나 두 경우 pruning을 하고나서 retrain으로 fine-tuning을 하면 정확도 손해를 보상받을 수 있다는 것을 보여준다
이 때 초록색 선과 갈색 선을 보면 retrain을 하고나서는 반대의 경향을 보인다.
즉 L2 regularization이 동일한 양의 pruning을 했을 때 정확도 손해가 덜해진다는 사실을 보여준다
심지어 마지막 빨간색 그래프는 iterative pruning을 한 것인데 그 경우 정확도 손해가 제일 적다는 것을 보여준다
결론은 retrain을 할수록 그리고 iterative pruning을 할수록 정확도 손해를 덜본다는 사실
그리고 pruning을 할때 retrain을 할 것이라면 되도록이면 L2 regularization을 하는 것이 더 좋다는 사실
5. regularization의 직관적인 이해
weight를 update하는 training과정은 loss를 최소화하는 과정
regularization term을 loss에 추가하면 weight가 커질수록 loss가 커지는 penalty를 부여
결과적으로 weight가 너무 커지지도 않게, 너무 작아지지도 않게하는 적당한 weight로 convergence시킴

검정색 점이 initialize된 초기 parameter
초기 parameter를 가지고 loss를 최소화시키는 parameter를 찾아가는 과정이 training과정
$\lambda=0$으로 L2 regularization을 수행하지 않으면 training시 data에 overfitting된 파란색 optimal?한 parameter로 수렴할 것
그러나 L2 regularization term을 loss에 추가하면 weight가 너무 커지지 않게 방지하면서
data에 너무 overfitting되지 않게 만들어서 일반화능력이 있는 빨간색 점의 parameter로 수렴함
극단적으로 초록색의 0,0,0,...0으로도 가지 않는 이유는 그 지점도 loss가 매우 큰 지점임
regularization이 이렇게 parameter에 따라 depend하므로 parameter중 중요하지 않은 것을 제거하는 pruning은 regularization의 영향을 받을 수 밖에 없다.
6. speed and accuracy tradeoff
pruning을 하여 size를 줄이면 속도는 빨라질 것이지만 그에 따라 정확도인 accuracy는 어느정도 손해볼 것이다

위 그래프를 보면 pruning을 하면 기본적으로 parameter 수가 줄어든다는 사실을 볼 수 있음 mobilenet은 없긴한디..
심지어 계산량(FLOPs)도 줄어든다는 사실을 볼 수 있음
그런데 pruning model이 대체적으로 original model에 비해 정확도가 조금 낮음.. 그렇게 낮지는 않은데??
efficientnet은 최신기술이라 pruning을 안해봤다고 논문에서 언급함

efficientnet pruning을 안한 이유로 최신기술이라고… 근데 그러면 왜 쓴거야??? 그냥 pruning을 안해도 계산량에 비해 성능이 압도적이다 이건가
'딥러닝 > light weight modeling' 카테고리의 다른 글
| iterative pruning의 여러가지 변형 버전 알아보기 (0) | 2022.11.14 |
|---|---|
| pruning을 하는 여러가지 방법들 (0) | 2022.11.12 |
| 딥러닝 경량화 기법 pruning은 무엇이고 왜 등장했는가 (0) | 2022.11.09 |
| CPU,GPU,TPU,.... 여러가지 processing unit 알아보기 (0) | 2022.11.07 |
| 컴퓨터 과학에서 말하는 compression의 개념 (0) | 2022.11.06 |

