1. idea
MobileNet v1의 핵심 아이디어는 depthwise separable convolution
일반적인 convolution 연산을 2단계로 분리하여 depthwise convolution을 수행하고 pointwise convolution을 수행
계산량이 일반적인 convolution에 비해 줄어드는데 정확도는 오히려 좋아지거나?? 아주 조금 손해를 보는 정도
2. 일반적인 convolution
M channel 커널이 M channel input에 한번에 convolution을 수행함
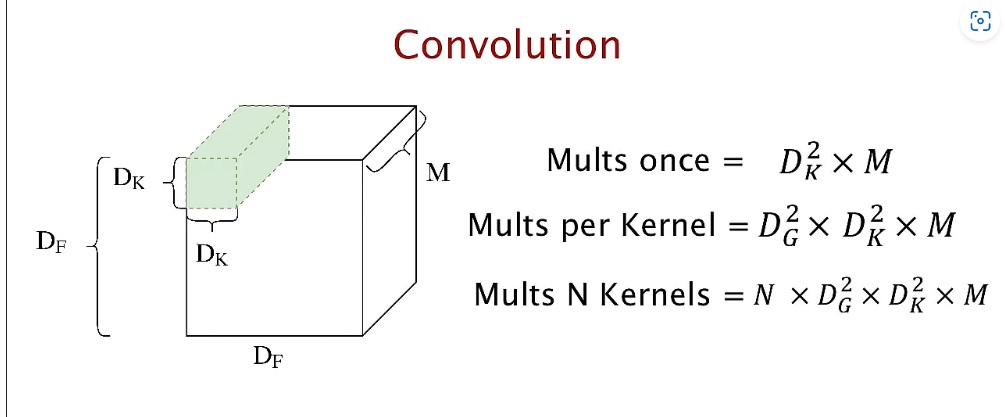
원래 depthwise separable이 연산량이 높을수도 있다고 생각했는데 지금부터 항상 감소한다는 것을 증명할 것이다.
kernel size를 $D_{k} \times D_{k}^{'}$, input channel 수를 M, output channel 수를 N이라 하고 output feature map size를 $D_{o} \times D_{o}^{'}$이라 하자.
convolution 1번 연산에 output feature map 1 pixel을 만드므로 output feature map size $D_{o} \times D_{o}^{'}$만큼 연산하면 map 1개를 만들 수 있고 N번 하면 output 하나를 만들 수 있다.

kernel 크기 $D_{k} \times D_{k}^{'} \times M$가 N개 있어야 N 채널 가지는 output이 나오므로
$D_{k} \times D_{k}^{'} \times M \times N$개의 parameter가 있고
여기에 output map 1개를 만드는 계산비용 $D_{o} \times D_{o}^{'}$을 곱하면 총 비용은
$D_{k} \times D_{k}^{'} \times M \times N \times D_{o} \times D_{o}^{'}$
3. depthwise convolution
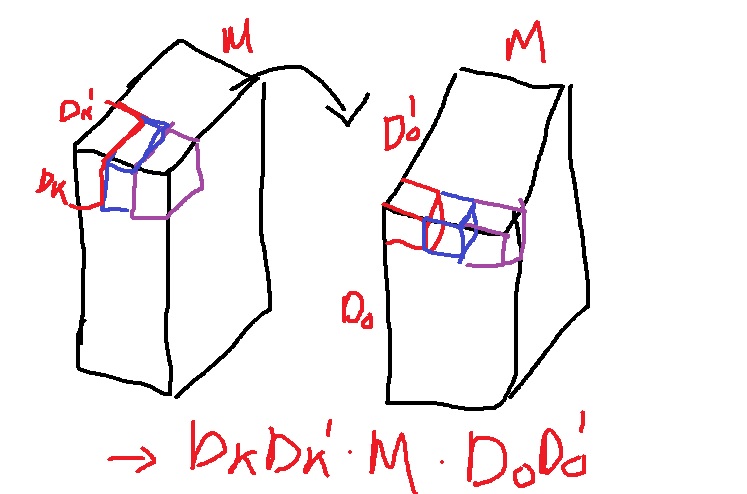
그림과 같이 channel이 1인 kernel을 M개 준비해서 하나의 kernel spatial space $D_{k} \times D_{k}^{'}$에 M번 나눠서 수행하는 방법

kernel을 채널축 1개씩 convolution 연산을 하는 방법
kernel $D_{k} \times D_{k}^{'}$이 1 pixel을 만드는데 이것을 $D_{o} \times D_{o}^{'} \times M$개 만들어야 하므로 총 비용은 $D_{k} \times D_{k}^{'} \times M \times D_{o} \times D_{o}^{'}$
4. pointwise convolution
depthwise convolution 결과에 $1 \times 1$ convolution을 수행하는 방법
N개의 커널을 이용하면 채널이 N이 된다

M개의 channel축을 1개로 convolution하여 만드는 연산
이것을 총 N번 하여 최종 output을 만들어냄
M개가 1개의 pixel이 되는데 $D_{o} \times D_{o}^{'}$만큼 해야 하나의 map이 나오고 N번 해야 $D_{o} \times D_{o}^{'} \times N$크기의 output이 나오니 최종 비용은 $M \times N \times D_{o} \times D_{o}^{'}$

5. depthwise separable convolution
depthwise convolution과 pointwise convolution의 합이므로 총 계산 비용은
$$D_{k} \times D_{k}^{'} \times M \times D_{o} \times D_{o}^{'} + M \times N \times D_{o} \times D_{o}^{'} = (D_{k} \times D_{k}^{'} + N) \times D_{o} \times D_{o}^{'} \times M$$
일반적인 convolution 비용은 $D_{k} \times D_{k}^{'} \times M \times N \times D_{o} \times D_{o}^{'}$
depthwise separable / regular convolution 을 계산하면..
$$\frac{1}{N} + \frac{1}{D_{k} \times D_{k}^{'}}$$
그러니까 depthwise separable의 계산 비용은 일반적인 convolution에 비해서 $\frac{1}{N} + \frac{1}{D_{k} \times D_{k}^{'}}$만큼 감소했다
여기서 재밌는 점은 일반적인 convolution의 $D_{k} \times D_{k}^{'} \times N$의 곱연산에서 depthwise separable convoltuon으로 변하면서 $D_{k} \times D_{k}^{'} +N $ 합연산으로 바뀌었다는 점
보통 곱연산에서 합연산으로 바꾸면서 계산 이득을 취하는 log likelihood와 비슷한 근본 원리가 숨어있다
Depthwise separable convolution 연산 - gaussian37
Depthwise separable convolution 연산
gaussian37's blog
gaussian37.github.io
'딥러닝 > light weight modeling' 카테고리의 다른 글
| CPU,GPU,TPU,.... 여러가지 processing unit 알아보기 (0) | 2022.11.07 |
|---|---|
| 컴퓨터 과학에서 말하는 compression의 개념 (0) | 2022.11.06 |
| 컴퓨터의 근본 원리가 된 finite state machine 개념 익히기 (0) | 2022.11.04 |
| 머신러닝 관점에서 information transmission (0) | 2022.11.03 |
| 딥러닝에서 parameter search하는 gradient descent와 기하학적 의미 (0) | 2022.11.02 |

