1. 문제
5648. [모의 SW 역량테스트] 원자 소멸 시뮬레이션
SW Expert Academy
SW 프로그래밍 역량 강화에 도움이 되는 다양한 학습 컨텐츠를 확인하세요!
swexpertacademy.com
맵에 배치된 원자들이 동시에 1초에 1만큼 이동하고, 방향을 바꾸지 않는다.
원자들이 소멸되면서 방출하는 에너지의 총합을 구하는 문제
2. 풀이
이전에 배운 미생물 격리 문제에서 얻은 시뮬레이션의 기본 방법으로 시뮬레이션을 해보면 된다
문제를 보면 1초에 1만큼 동시에 이동하니까, 1초에 1씩 이동시킨다고 생각하면 될까? 했는데
1.5초에 충돌한다고 예시에 나와있더라

그러면 ... 아니 1초마다 말고 0.x초마다 반복문을 해야한다는거여??
아니 근데 0.x초마다 반복문을 어떻게 돌리냐?
하지만 조금만 생각해보면, 1초에 1만큼 동시에 같은 속도로 이동하기 때문에 원자는 0.5초 단위로만 충돌이 가능하다
같은 속도로 이동하는데

이렇게 0.2, 0.8에서 충돌하는건 불가능하다는 말이야
그러니까 0.5초 단위로 시뮬레이션을 수행하면 되겠다.
그러면 최초 dict에 원자 위치를 key로 방향과 에너지를 value로 해서 모든 원자를 배치하자
##직관적인 시뮬레이션
T = int(input())
for tc in range(1,T+1):
n = int(input())
before_maps = {} ##시뮬레이션 시작 전에 배치된 원자 지도
for _ in range(n):
x,y,d,k = map(int,input().split())
before_maps[(x,y)] = [(d,k)] ##원자 위치를 key로 방향과 에너지를 value로 하는 dictionary 생성
0.5초 단위로 시뮬레이션을 할거니까, 움직이는 최소 거리는 0.5씩으로 할거야
##시뮬레이션 시작
##최초 정수 위치에 주어지고 모든 원자가 1초에 1만큼 이동하므로
##만날 수 있는 최소한의 가능성은 0.5초 단위로 움직일때이다.
delta = [[0.0,0.5],[0.0,-0.5],[-0.5,0.0],[0.5,0.0]] ##상,하,좌,우
ans = 0 ##충돌후 에너지 총합
그런데 이 문제에서 원자들의 최초 위치 범위 제한이 주어진다
-1000과 1000사이이므로, 0.5초씩 움직인다면..

최대 4000번까지는 시뮬레이션을 수행해야한다는 것도 파악할 수 있다
그래서 최대 4000번 반복문을 돌리고
0.5초씩 움직여본다
before_maps와 after_maps를 이용하라고 배웠지
0.5초 움직여서 after_maps에 이동한 원자가 존재한다면 충돌시켜야하니 리스트로 만들어서 저장하고
원자가 없다면..새로 리스트를 만들어서 저장시키고
리스트로 만드는건 여러 원자가 한번에 부딪힐수도 있거든
##0.5초씩 움직이고 최초 위치가 -1000이상 1000이하로 주어지므로
##최대한으로 늦게 부딪히는 가능성은 4000번이다.
##예를 들어 (-1000,1000)이 아래로 가고 (1000,-1000) 좌로 갈때 부딪히는 원자
for _ in range(4000):
after_maps = {} #0.5초 후에 원자들의 배치
##0.5초 움직이기
for (x,y),value in before_maps.items(): ##원자위치, [(방향,에너지)]
for d,k in value:
dx = x + delta[d][0]
dy = y + delta[d][1] ##0.5초씩 움직인 좌표
if after_maps.get((dx,dy),0) == 0: ##움직인 좌표에 아무것도 존재하지 않는다면..
after_maps[(dx,dy)] = [(d,k)] ##새로 리스트를 만들어 저장
else: ##이미 움직인 좌표에 원자가 존재한다면..
after_maps[(dx,dy)].append((d,k)) ##방향과 에너지를 넣는다
0.5초 단위로 움직인 after_maps에서 이제 충돌 가능성이 있는 경우가 있다면
충돌 시켜서 에너지를 구해야함
##충돌 에너지 계산
del_point = [] ##충돌 후 dictionary에서 key를 삭제하기 위해
for (x,y),value in after_maps.items(): ##충돌위치, (원자 방향,에너지)의 리스트
if len(value) >= 2: ## 같은 위치에 2개 이상 존재한다면 충돌했다는 뜻이므로..
del_point.append((x,y)) ##해당 위치를 삭제하기 위해 임시로 저장
for d,k in value:
ans += k ##모든 에너지 방출 합
after_maps를 다시 순회해서 리스트 길이가 2이상이면, 충돌했다는 뜻이니까, 삭제 포인트에 key를 따로 저장해두고
에너지의 합을 구해서 저장
##충돌 포인트를 dictionary에서 삭제
##for문 도는 중에 dictionary의 key를 삭제할 수가 없어서 따로 모아놓은다음에 삭제함
for x,y in del_point:
del after_maps[(x,y)] ##충돌한 위치 삭제
충돌했다면, 딕셔너리에서 해당 key를 삭제해줘야 원자가 소멸되겠지
순회하는 중에 key를 삭제할 수는 없어서 나중에 이런식으로 따로 삭제해줘야함
충돌하고 소멸시켰더니, 필드 위에 원자가 1개 이상 존재하면 더 해볼필요는 없겠지
충돌할 일이 없으니까
그리고 before_maps를 다시 초기화해서, 다음 시뮬레이션으로 넘겨줘야지
##직관적인 시뮬레이션
T = int(input())
for tc in range(1,T+1):
n = int(input())
before_maps = {} ##시뮬레이션 시작 전에 배치된 원자 지도
for _ in range(n):
x,y,d,k = map(int,input().split())
before_maps[(x,y)] = [(d,k)] ##원자 위치를 key로 방향과 에너지를 value로 하는 dictionary 생성
##시뮬레이션 시작
##최초 정수 위치에 주어지고 모든 원자가 1초에 1만큼 이동하므로
##만날 수 있는 최소한의 가능성은 0.5초 단위로 움직일때이다.
delta = [[0.0,0.5],[0.0,-0.5],[-0.5,0.0],[0.5,0.0]] ##상,하,좌,우
ans = 0 ##충돌후 에너지 총합
##0.5초씩 움직이고 최초 위치가 -1000이상 1000이하로 주어지므로
##최대한으로 늦게 부딪히는 가능성은 4000번이다.
##예를 들어 (-1000,1000)이 아래로 가고 (1000,-1000) 좌로 갈때 부딪히는 원자
for _ in range(4000):
after_maps = {} #0.5초 후에 원자들의 배치
##0.5초 움직이기
for (x,y),value in before_maps.items(): ##원자위치, [(방향,에너지)]
for d,k in value:
dx = x + delta[d][0]
dy = y + delta[d][1] ##0.5초씩 움직인 좌표
if after_maps.get((dx,dy),0) == 0: ##움직인 좌표에 아무것도 존재하지 않는다면..
after_maps[(dx,dy)] = [(d,k)] ##새로 리스트를 만들어 저장
else: ##이미 움직인 좌표에 원자가 존재한다면..
after_maps[(dx,dy)].append((d,k)) ##방향과 에너지를 넣는다
##충돌 에너지 계산
del_point = [] ##충돌 후 dictionary에서 key를 삭제하기 위해
for (x,y),value in after_maps.items(): ##충돌위치, (원자 방향,에너지)의 리스트
if len(value) >= 2: ## 같은 위치에 2개 이상 존재한다면 충돌했다는 뜻이므로..
del_point.append((x,y)) ##해당 위치를 삭제하기 위해 임시로 저장
for d,k in value:
ans += k ##모든 에너지 방출 합
##충돌 포인트를 dictionary에서 삭제
##for문 도는 중에 dictionary의 key를 삭제할 수가 없어서 따로 모아놓은다음에 삭제함
for x,y in del_point:
del after_maps[(x,y)] ##충돌한 위치 삭제
##필드에 원자가 하나이하만 존재한다면.. 더 이상 충돌할 수 없으므로
##시뮬레이션 중단
if len(after_maps.keys()) <= 1:
break
##다음 시뮬레이션으로 초기화
before_maps = after_maps
print('#'+str(tc),ans)
3. 최적화해보기
최초 원자들이 -1000과 1000이내로 주어지기 때문에
원자들이 0.5초 단위로 4000번 이동하는 동안에 어떤 원자는 1000이나 -1000을 넘어갈 수 있거든
원자들은 방향을 바꾸지 않기때문에, 1000을 넘어가는 원자는 그냥 소멸시켜버린다
0.5초 단위로 이동시켰을때 dx,dy가 1000과 -1000이내에 존재하는 경우에만 after_maps에 추가시킨다.
##직관적인 시뮬레이션
##탐색 범위를 줄여 최적화
T = int(input())
for tc in range(1,T+1):
n = int(input())
before_maps = {} ##시뮬레이션 시작 전에 배치된 원자 지도
for _ in range(n):
x,y,d,k = map(int,input().split())
before_maps[(x,y)] = [(d,k)] ##원자 위치를 key로 방향과 에너지를 value로 하는 dictionary 생성
##시뮬레이션 시작
##최초 정수 위치에 주어지고 모든 원자가 1초에 1만큼 이동하므로
##만날 수 있는 최소한의 가능성은 0.5초 단위로 움직일때이다.
delta = [[0.0,0.5],[0.0,-0.5],[-0.5,0.0],[0.5,0.0]] ##상,하,좌,우
ans = 0 ##충돌후 에너지 총합
##0.5초씩 움직이고 최초 위치가 -1000이상 1000이하로 주어지므로
##최대한으로 늦게 부딪히는 가능성은 4000번이다.
##예를 들어 (-1000,1000)이 아래로 가고 (1000,-1000) 좌로 갈때 부딪히는 원자
for _ in range(4000):
after_maps = {} #0.5초 후에 원자들의 배치
##0.5초 움직이기
for (x,y),value in before_maps.items(): ##원자위치, [(방향,에너지)]
for d,k in value:
dx = x + delta[d][0]
dy = y + delta[d][1] ##0.5초씩 움직인 좌표
##최초 주어진 위치가 1000이내라서
##원자들은 방향을 바꾸지 않으므로
##1000을 넘어가는 원자는 충돌 가능성이 없다
if dx <= 1000 and dx >=-1000 and dy <=1000 and dy >= -1000:
if after_maps.get((dx,dy),0) == 0: ##움직인 좌표에 아무것도 존재하지 않는다면..
after_maps[(dx,dy)] = [(d,k)] ##새로 리스트를 만들어 저장
else: ##이미 움직인 좌표에 원자가 존재한다면..
after_maps[(dx,dy)].append((d,k)) ##방향과 에너지를 넣는다
##충돌 에너지 계산
del_point = [] ##충돌 후 dictionary에서 key를 삭제하기 위해
for (x,y),value in after_maps.items(): ##충돌위치, (원자 방향,에너지)의 리스트
if len(value) >= 2: ## 같은 위치에 2개 이상 존재한다면 충돌했다는 뜻이므로..
del_point.append((x,y)) ##해당 위치를 삭제하기 위해 임시로 저장
for d,k in value:
ans += k ##모든 에너지 방출 합
##충돌 포인트를 dictionary에서 삭제
##for문 도는 중에 dictionary의 key를 삭제할 수가 없어서 따로 모아놓은다음에 삭제함
for x,y in del_point:
del after_maps[(x,y)] ##충돌한 위치 삭제
##필드에 원자가 하나이하만 존재한다면.. 더 이상 충돌할 수 없으므로
##시뮬레이션 중단
if len(after_maps.keys()) <= 1:
break
##다음 시뮬레이션으로 초기화
before_maps = after_maps
print('#'+str(tc),ans)
4. 최적화해보기 2
위 풀이는 각각 13초, 7초정도 걸린다
근데 0.5초 단위로 부딪힐때까지 4000번이나 돌리는게 아쉬울 수 있다
더욱 빠르게 하는 방법은 충돌 가능성이 있다면 그냥 바로 충돌시켜버리면 된다
그래서 시뮬레이션하지 않고 최초에 원자들의 리스트를 받아서,
2개를 뽑아 실제로 충돌이 가능한지 모든 조합을 검사한다
원자 간의 충돌 가능성은 다음과 같다
y좌표가 서로 같고 좌,우로 움직이는 경우
충돌 시간은 어떻게 구할 수 있을까? 둘 사이 거리의 절반으로 구할 수 있겠지?

x좌표가 서로 같고 상,하로 움직이는 경우.. 역시 충돌 시간은 둘 사이 거리의 절반으로

직각으로 충돌하는 경우
x+y가 서로 같거나, x-y가 서로 같거나
충돌 시간은? x축으로 이동 거리만큼이 충돌 시간이겠지
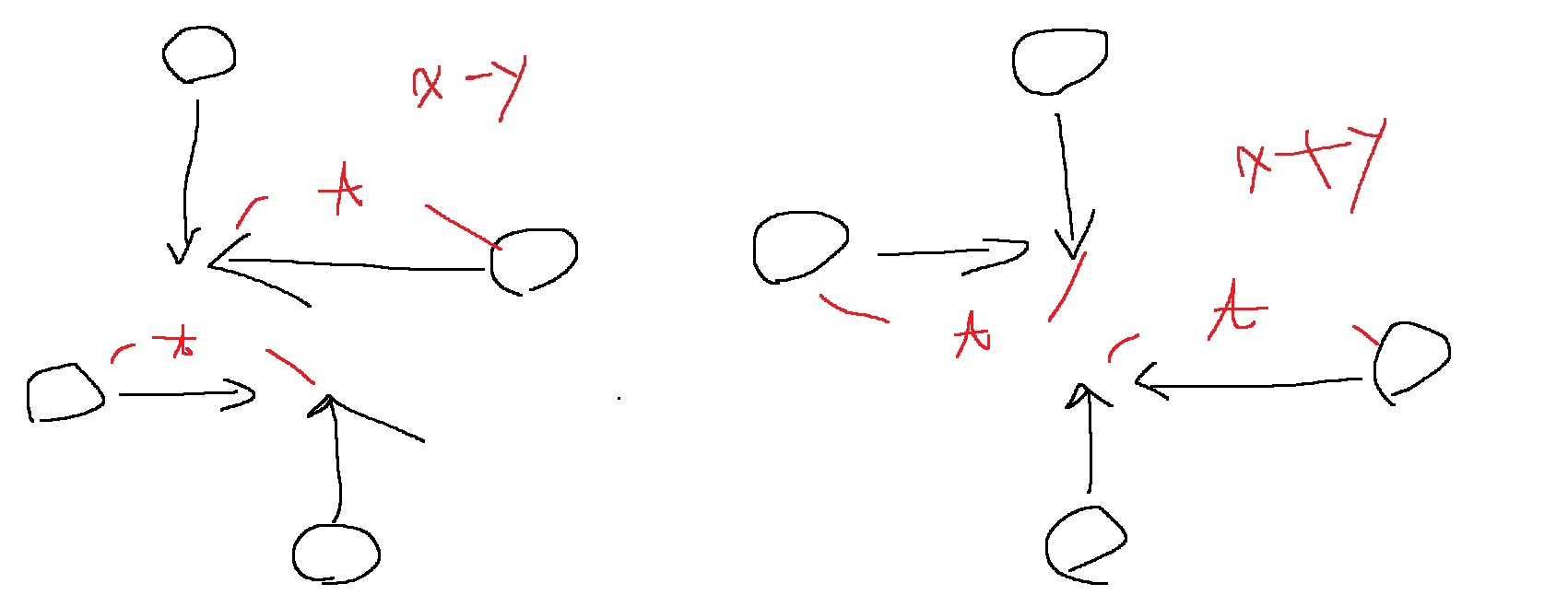
위와 같은 경우를 모두 찾아본다
(충돌위치,충돌시간)을 key로 해당 위치와 시간에 충돌하는 모든 원자들의 리스트를 value로
왼쪽에 있냐, 오른쪽에 있냐 위에 있냐 아래에 있냐... 모든 경우를 잘 고려해야함
##시뮬레이션 하지 않고 충돌 가능한 경우를 모두 찾아 한번에 처리
T = int(input())
for tc in range(1,T+1):
n = int(input())
atom_list = [list(map(int,input().split())) for _ in range(n)] ##원자들의 리스트
##원자들 간의 충돌 가능성을 모두 찾는다
##상,하로 움직이는데 x좌표가 같은 경우
##좌,우로 움직이는데 y좌표가 같은 경우
##x+y가 같은 경우(직각 충돌)
##x-y가 같은 경우(직각 충돌)
colide_candidate = {} ##충돌 가능한 후보를 저장한 사전
##n개중에 2개를 뽑은 모든 조합을 조사해서 충돌 가능한 모든 경우를 찾는다
for i in range(n-1):
x1,y1,d1,k1 = atom_list[i]
for j in range(i+1,n):
x2,y2,d2,k2 = atom_list[j]
if x1 == x2: ##x좌표가 서로 같다면..
colide_t = abs((y2-y1)/2) ##충돌 시간
if y1 > y2: ## 첫번째가 위에 있는 경우 하,상이면 충돌가능
if d1 == 1 and d2 == 0:
if colide_candidate.get((x1,(y1+y2)/2,colide_t),0) == 0:
colide_candidate[(x1,(y1+y2)/2,colide_t)] = [(i,k1),(j,k2)] ##충돌위치, 충돌시간을 key로 하고 (원자 고유번호,에너지)를 리스트로
else:
colide_candidate[(x1,(y1+y2)/2,colide_t)].append((i,k1))
colide_candidate[(x1,(y1+y2)/2,colide_t)].append((j,k2))
else: ##두번째 원자가 위에 있는 경우, 상,하이면 충돌 가능
if d1 == 0 and d2 == 1:
if colide_candidate.get((x1,(y1+y2)/2,colide_t),0) == 0:
colide_candidate[(x1,(y1+y2)/2,colide_t)] = [(i,k1),(j,k2)]
else:
colide_candidate[(x1,(y1+y2)/2,colide_t)].append((i,k1))
colide_candidate[(x1,(y1+y2)/2,colide_t)].append((j,k2))
elif y1 == y2: ##y좌표가 서로 같다면...
colide_t = abs((x2-x1)/2) ##충돌 시간
if x1 > x2: ##첫번째 원자가 오른쪽에 있다면..
if d1 == 2 and d2 == 3: ##좌,우로 향하면 충돌 가능
if colide_candidate.get(((x1+x2)/2,y1,colide_t),0) == 0:
colide_candidate[((x1+x2)/2,y1,colide_t)] = [(i,k1),(j,k2)]
else:
colide_candidate[((x1+x2)/2,y1,colide_t)].append((i,k1))
colide_candidate[((x1+x2)/2,y1,colide_t)].append((j,k2))
else: ##두번째 원자가 오른쪽에 있다면.. 우,좌로 향하면 충돌 가능
if d1 == 3 and d2 == 2: ##우,좌로 향하면 충돌 가능
if colide_candidate.get(((x1+x2)/2,y1,colide_t),0) == 0:
colide_candidate[((x1+x2)/2,y1,colide_t)] = [(i,k1),(j,k2)]
else:
colide_candidate[((x1+x2)/2,y1,colide_t)].append((i,k1))
colide_candidate[((x1+x2)/2,y1,colide_t)].append((j,k2))
elif x1-y1 == x2-y2: ##x-y가 서로 같으면 충돌 가능
colide_t = abs(x2-x1) ##충돌 시간
if x1 > x2: ##첫번째가 오른쪽에 존재한다면..
if (d1 == 2 and d2 == 0):
if colide_candidate.get((x2,y1,colide_t),0) == 0:
colide_candidate[(x2,y1,colide_t)] = [(i,k1),(j,k2)]
else:
colide_candidate[(x2,y1,colide_t)].append((i,k1))
colide_candidate[(x2,y1,colide_t)].append((j,k2))
elif d1 == 1 and d2 == 3:
if colide_candidate.get((x1,y2,colide_t),0) == 0:
colide_candidate[(x1,y2,colide_t)] = [(i,k1),(j,k2)]
else:
colide_candidate[(x1,y2,colide_t)].append((i,k1))
colide_candidate[(x1,y2,colide_t)].append((j,k2))
else:
if (d1 == 0 and d2 == 2):
if colide_candidate.get((x1,y2,colide_t),0) == 0:
colide_candidate[(x1,y2,colide_t)] = [(i,k1),(j,k2)]
else:
colide_candidate[(x1,y2,colide_t)].append((i,k1))
colide_candidate[(x1,y2,colide_t)].append((j,k2))
elif d1 == 3 and d2 == 1:
if colide_candidate.get((x2,y1,colide_t),0) == 0:
colide_candidate[(x2,y1,colide_t)] = [(i,k1),(j,k2)]
else:
colide_candidate[(x2,y1,colide_t)].append((i,k1))
colide_candidate[(x2,y1,colide_t)].append((j,k2))
elif x1+y1 == x2+y2: ##x+y가 서로 같으면 충돌 가능
colide_t = abs(x1-x2) ##충돌 시간
if x1 > x2: ##첫번째가 오른쪽에 존재한다면..
if (d1 == 2 and d2 == 1):
if colide_candidate.get((x2,y1,colide_t),0) == 0:
colide_candidate[(x2,y1,colide_t)] = [(i,k1),(j,k2)]
else:
colide_candidate[(x2,y1,colide_t)].append((i,k1))
colide_candidate[(x2,y1,colide_t)].append((j,k2))
elif d1 == 0 and d2 == 3:
if colide_candidate.get((x1,y2,colide_t),0) == 0:
colide_candidate[(x1,y2,colide_t)] = [(i,k1),(j,k2)]
else:
colide_candidate[(x1,y2,colide_t)].append((i,k1))
colide_candidate[(x1,y2,colide_t)].append((j,k2))
else:
if (d1 == 1 and d2 == 2):
if colide_candidate.get((x1,y2,colide_t),0) == 0:
colide_candidate[(x1,y2,colide_t)] = [(i,k1),(j,k2)]
else:
colide_candidate[(x1,y2,colide_t)].append((i,k1))
colide_candidate[(x1,y2,colide_t)].append((j,k2))
elif d1 == 3 and d2 == 0:
if colide_candidate.get((x2,y1,colide_t),0) == 0:
colide_candidate[(x2,y1,colide_t)] = [(i,k1),(j,k2)]
else:
colide_candidate[(x2,y1,colide_t)].append((i,k1))
colide_candidate[(x2,y1,colide_t)].append((j,k2))
else:
pass ##이외의 조합은 모두 충돌 불가능
충돌 에너지를 계산하는게 이제 생각보다 까다롭다
먼저 충돌은 충돌 시간이 빠른 순서대로 충돌이 일어날거다.
그러니까 충돌 후보들을 충돌 시간이 빠른 순서로 먼저 정렬을 수행한다
##충돌 처리를 하여 충돌 에너지를 계산
##충돌이 가능한 모든 조합을 선정했으면
##이제 시간이 빠른 순서대로 정렬함
sorted_candidate = sorted(colide_candidate.items(), key = lambda item: item[0][2])
근데 이제 이 후보를 순회해서 충돌 처리해서 에너지 합을 계산하면 될까?
그렇지 않다
충돌 처리를 하지 않고 모든 가능한 후보를 계산해서 넣어놨으니까
2초에 충돌한 원자 a가 (x,y)에 충돌한다면...
5초에 또 원자 a가 (z,w)에 충돌할 수도 있으니까
그렇지만 2초에 원자 a가 (x,y)에 충돌했다면... 5초에 또 충돌한다는건 말이 안된다
이런걸 처리하기 위해.. 충돌을 했다면 죽었다는 뜻으로 visited 배열을 만들거다
dead_atom = [0]*n ##이미 충돌해서 없어진 원자, 중복처리를 하기 위함
ans = 0 ##충돌 에너지 총합
이제 정렬된 후보를 처음부터 순회해서 충돌 처리를 수행하자
충돌 후보들을 순회했는데, dead_atom에 아직 표시되지 않은 원자라면... 아직은 충돌한 원자가 아니다.
그러니까 충돌시켜서 에너지를 저장해놓음
##충돌시작
for key,colide_atom in sorted_candidate: ##(충돌위치,충돌시간), (고유번호,에너지)의 리스트
energy = [] ##충돌한 에너지
cnt = 0 ##충돌 수
tmp = set() ##충돌한 원자들
for i,k in colide_atom:
if dead_atom[i] == 0: ##아직 충돌한 것이 아니라면..
dead_atom[i] = 1 ##충돌하여 소멸처리
cnt += 1 ##충돌한 원자수
energy.append(k) ##충돌한 원자의 방출 에너지
tmp.add(i) ##원자들의 고유번호 저장
근데 이게 문제가 뭐냐면... 2초에 충돌처리를 해버린 원자가 5초나 7초 9초에 또 들어있을 수가 있어서
그런 경우에는 충돌 처리를 하면 안되잖아
그랬더니... 5초에 충돌 가능한 후보 원자가 2개 있는데
이미 앞에서 충돌을 해버려가지고.. 충돌 가능한 후보 원자가 1개밖에 안남았어
이런 경우는 충돌한게 아니지
따라서 이런 경우도 고려해줘야함
그래서 충돌 처리를 할때 충돌한 원자 수를 세고, 충돌한 원자 번호를 임시 리스트에 넣어준다
실제로 충돌이 일어날려면, 충돌 처리를 한 원자가 2개 이상이어야한다
if cnt >= 2: ##충돌한 원자수가 2개 이상이면, 실제로 충돌이 일어났다
ans += sum(energy) ##에너지들의 합을 누적
else: ##충돌한 원자수가 1개 이하이면, 충돌하지 않았다.
for i in tmp: ##충돌하지 않았는데 임시로 저장한 고유번호가 충돌처리 되었으므로
dead_atom[i] = 0 ##다시 충돌할 수 있다고 원상복구
print('#'+str(tc),ans)
하지만 충돌한 원자수가 1개 이하라면, 앞에서 이미 충돌해버린 원자때문에 충돌할수가 없는것이다.
그런 경우에는 임시 리스트를 순회해서 dead_atom을 원상복구 시켜줘야한다
충돌한게 아니니까
##시뮬레이션 하지 않고 충돌 가능한 경우를 모두 찾아 한번에 처리
T = int(input())
for tc in range(1,T+1):
n = int(input())
atom_list = [list(map(int,input().split())) for _ in range(n)] ##원자들의 리스트
##원자들 간의 충돌 가능성을 모두 찾는다
##상,하로 움직이는데 x좌표가 같은 경우
##좌,우로 움직이는데 y좌표가 같은 경우
##x+y가 같은 경우(직각 충돌)
##x-y가 같은 경우(직각 충돌)
colide_candidate = {} ##충돌 가능한 후보를 저장한 사전
##n개중에 2개를 뽑은 모든 조합을 조사해서 충돌 가능한 모든 경우를 찾는다
for i in range(n-1):
x1,y1,d1,k1 = atom_list[i]
for j in range(i+1,n):
x2,y2,d2,k2 = atom_list[j]
if x1 == x2: ##x좌표가 서로 같다면..
colide_t = abs((y2-y1)/2) ##충돌 시간
if y1 > y2: ## 첫번째가 위에 있는 경우 하,상이면 충돌가능
if d1 == 1 and d2 == 0:
if colide_candidate.get((x1,(y1+y2)/2,colide_t),0) == 0:
colide_candidate[(x1,(y1+y2)/2,colide_t)] = [(i,k1),(j,k2)] ##충돌위치, 충돌시간을 key로 하고 (원자 고유번호,에너지)를 리스트로
else:
colide_candidate[(x1,(y1+y2)/2,colide_t)].append((i,k1))
colide_candidate[(x1,(y1+y2)/2,colide_t)].append((j,k2))
else: ##두번째 원자가 위에 있는 경우, 상,하이면 충돌 가능
if d1 == 0 and d2 == 1:
if colide_candidate.get((x1,(y1+y2)/2,colide_t),0) == 0:
colide_candidate[(x1,(y1+y2)/2,colide_t)] = [(i,k1),(j,k2)]
else:
colide_candidate[(x1,(y1+y2)/2,colide_t)].append((i,k1))
colide_candidate[(x1,(y1+y2)/2,colide_t)].append((j,k2))
elif y1 == y2: ##y좌표가 서로 같다면...
colide_t = abs((x2-x1)/2) ##충돌 시간
if x1 > x2: ##첫번째 원자가 오른쪽에 있다면..
if d1 == 2 and d2 == 3: ##좌,우로 향하면 충돌 가능
if colide_candidate.get(((x1+x2)/2,y1,colide_t),0) == 0:
colide_candidate[((x1+x2)/2,y1,colide_t)] = [(i,k1),(j,k2)]
else:
colide_candidate[((x1+x2)/2,y1,colide_t)].append((i,k1))
colide_candidate[((x1+x2)/2,y1,colide_t)].append((j,k2))
else: ##두번째 원자가 오른쪽에 있다면.. 우,좌로 향하면 충돌 가능
if d1 == 3 and d2 == 2: ##우,좌로 향하면 충돌 가능
if colide_candidate.get(((x1+x2)/2,y1,colide_t),0) == 0:
colide_candidate[((x1+x2)/2,y1,colide_t)] = [(i,k1),(j,k2)]
else:
colide_candidate[((x1+x2)/2,y1,colide_t)].append((i,k1))
colide_candidate[((x1+x2)/2,y1,colide_t)].append((j,k2))
elif x1-y1 == x2-y2: ##x-y가 서로 같으면 충돌 가능
colide_t = abs(x2-x1) ##충돌 시간
if x1 > x2: ##첫번째가 오른쪽에 존재한다면..
if (d1 == 2 and d2 == 0):
if colide_candidate.get((x2,y1,colide_t),0) == 0:
colide_candidate[(x2,y1,colide_t)] = [(i,k1),(j,k2)]
else:
colide_candidate[(x2,y1,colide_t)].append((i,k1))
colide_candidate[(x2,y1,colide_t)].append((j,k2))
elif d1 == 1 and d2 == 3:
if colide_candidate.get((x1,y2,colide_t),0) == 0:
colide_candidate[(x1,y2,colide_t)] = [(i,k1),(j,k2)]
else:
colide_candidate[(x1,y2,colide_t)].append((i,k1))
colide_candidate[(x1,y2,colide_t)].append((j,k2))
else:
if (d1 == 0 and d2 == 2):
if colide_candidate.get((x1,y2,colide_t),0) == 0:
colide_candidate[(x1,y2,colide_t)] = [(i,k1),(j,k2)]
else:
colide_candidate[(x1,y2,colide_t)].append((i,k1))
colide_candidate[(x1,y2,colide_t)].append((j,k2))
elif d1 == 3 and d2 == 1:
if colide_candidate.get((x2,y1,colide_t),0) == 0:
colide_candidate[(x2,y1,colide_t)] = [(i,k1),(j,k2)]
else:
colide_candidate[(x2,y1,colide_t)].append((i,k1))
colide_candidate[(x2,y1,colide_t)].append((j,k2))
elif x1+y1 == x2+y2: ##x+y가 서로 같으면 충돌 가능
colide_t = abs(x1-x2) ##충돌 시간
if x1 > x2: ##첫번째가 오른쪽에 존재한다면..
if (d1 == 2 and d2 == 1):
if colide_candidate.get((x2,y1,colide_t),0) == 0:
colide_candidate[(x2,y1,colide_t)] = [(i,k1),(j,k2)]
else:
colide_candidate[(x2,y1,colide_t)].append((i,k1))
colide_candidate[(x2,y1,colide_t)].append((j,k2))
elif d1 == 0 and d2 == 3:
if colide_candidate.get((x1,y2,colide_t),0) == 0:
colide_candidate[(x1,y2,colide_t)] = [(i,k1),(j,k2)]
else:
colide_candidate[(x1,y2,colide_t)].append((i,k1))
colide_candidate[(x1,y2,colide_t)].append((j,k2))
else:
if (d1 == 1 and d2 == 2):
if colide_candidate.get((x1,y2,colide_t),0) == 0:
colide_candidate[(x1,y2,colide_t)] = [(i,k1),(j,k2)]
else:
colide_candidate[(x1,y2,colide_t)].append((i,k1))
colide_candidate[(x1,y2,colide_t)].append((j,k2))
elif d1 == 3 and d2 == 0:
if colide_candidate.get((x2,y1,colide_t),0) == 0:
colide_candidate[(x2,y1,colide_t)] = [(i,k1),(j,k2)]
else:
colide_candidate[(x2,y1,colide_t)].append((i,k1))
colide_candidate[(x2,y1,colide_t)].append((j,k2))
else:
pass ##이외의 조합은 모두 충돌 불가능
##충돌 처리를 하여 충돌 에너지를 계산
##충돌이 가능한 모든 조합을 선정했으면
##이제 시간이 빠른 순서대로 정렬함
sorted_candidate = sorted(colide_candidate.items(), key = lambda item: item[0][2])
dead_atom = [0]*n ##이미 충돌해서 없어진 원자, 중복처리를 하기 위함
ans = 0 ##충돌 에너지 총합
##충돌시작
for key,colide_atom in sorted_candidate: ##(충돌위치,충돌시간), (고유번호,에너지)의 리스트
energy = [] ##충돌한 에너지
cnt = 0 ##충돌 수
tmp = set() ##충돌한 원자들
for i,k in colide_atom:
if dead_atom[i] == 0: ##아직 충돌한 것이 아니라면..
dead_atom[i] = 1 ##충돌하여 소멸처리
cnt += 1 ##충돌한 원자수
energy.append(k) ##충돌한 원자의 방출 에너지
tmp.add(i) ##원자들의 고유번호 저장
if cnt >= 2: ##충돌한 원자수가 2개 이상이면, 실제로 충돌이 일어났다
ans += sum(energy) ##에너지들의 합을 누적
else: ##충돌한 원자수가 1개 이하이면, 충돌하지 않았다.
for i in tmp: ##충돌하지 않았는데 임시로 저장한 고유번호가 충돌처리 되었으므로
dead_atom[i] = 0 ##다시 충돌할 수 있다고 원상복구
print('#'+str(tc),ans)
이러면 훨씬 더 빠르게 문제를 풀수 있지만.. 모든 경우를 실수없이 구하는게 쉽지 않다
그리고 실제 충돌할때 충돌 처리를 수행하고, 충돌이 실제로 일어난건지, 일어나지 않았으면 원상복구 시키는게 쉽지가 않다
5. 되돌아보기
처음에 애를 먹었지만.. 시뮬레이션 기본을 좀 배우니 생각보다 쉽게 풀었다
before_maps, after_maps 잘 이용해보고
빠른 시간으로 정렬해서 앞에서 충돌처리를 하면 dead_atom이라는 visited 배열을 이용해서 충돌 처리를 해두면
뒤에 있는 충돌 후보에서 충돌 처리 안일어나게 할수 있는데
이 과정에서 실제로 충돌이 일어나는지 아닌지도 검사했어야했던 디테일
충돌 개수까지 세서 2개 이상이어야 충돌이 실제로 일어난거였다는...
'알고리즘 > 구현,시뮬레이션' 카테고리의 다른 글
| 조금 더 어려운 시뮬레이션 연습하기 -미세먼지 안녕!- (0) | 2022.11.08 |
|---|---|
| deque도 인덱스로 접근해서 원소 수정이 가능하다 -컨베이어 벨트 위의 로봇- (0) | 2022.11.07 |
| 성실하게 시뮬레이션 구현하기.. -로봇 청소기- (0) | 2022.11.03 |
| 시뮬레이션의 기본을 배우는 문제 -미생물 격리- (0) | 2022.10.05 |
| deque를 이용하면 회전이 가능하다 -보물상자 비밀번호- (0) | 2022.09.21 |

