1. 문제
n개의 점이 일정한 간격으로 각 줄마다 n개의 줄이 존재하는 n*n 체스판이 있다고 하자.
n*n 체스판에서 서로 다른 네개의 점을 이어 만든 정사각형의 개수는 몇개일까?
선분을 이을 때 선분 중간에 존재하는 점은 개수로 세지 않는다.
예를 들어 n=3이면 6개 존재하고 n=4이면 20개 존재한다.

n은 2 이상의 자연수
2. 풀이
이런 문제가 나오면 규칙이 있겠구나 이렇게 생각하고 규칙을 찾으면 된다
프로그래밍을 해서 정사각형을 일일이 세도록 만들수는 없을거니까
근데 사실 규칙을 찾을려면 정사각형의 개수를 정확하게 세야하는데 그것이 절대 쉬운건 아니다
규칙을 찾겠다는 생각부터 한 것이 분명 한단계 발전한거
2가지로 나눠 생각할 수 있다
빨간색으로 된 격자형 정사각형이랑 파란색으로 된 기울어진 정사각형
격자형 정사각형은 규칙을 발견하기가 쉽다

1*1 정사각형은 $1^2$
2*2 정사각형은 $2^2$
3*3 정사각형은 $3^2$
... n*n 체스판에서 존재하는 모든 격자형 정사각형의 개수는 $$\sum_{k=2}^{n} (k-1)^2 = \frac{n(n-1)(2n-1)}{6}$$
기울어진 정사각형은 몇개인가??

n=4인 경우까지는 찾기 쉬운데 n=5인 경우부터는 쉽지가 않다

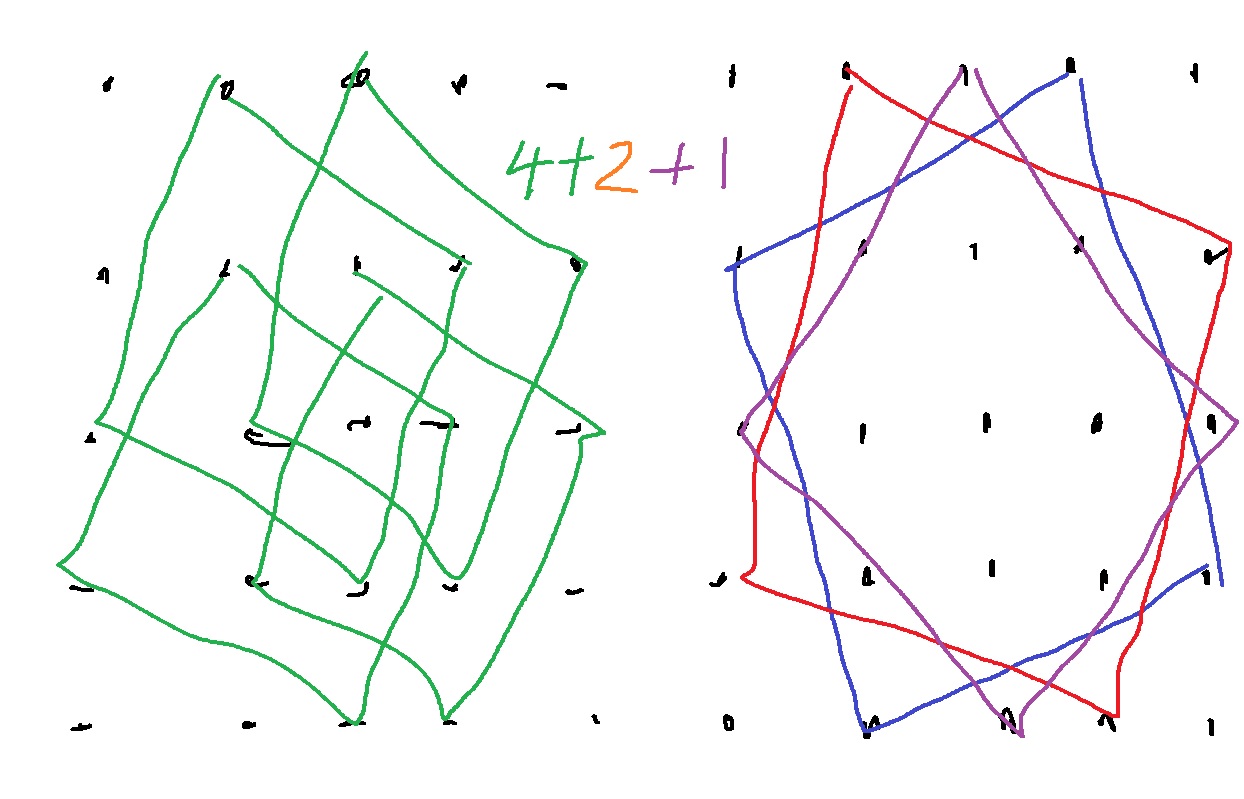
n=5인 경우 기울어진 정사각형이 총 20개 존재한다.
격자형 정사각형은 $1^2+2^2+3^2+4^2=30$
그래서 총 정사각형의 개수는 50개일 거임
나 같은 경우 그림5의 보라색 부분 1개를 빼먹었다
그러면 기울어진 정사각형의 개수에 대한 수열이 0,1,6,20,.... 이렇게 되는데
n=2인 경우 정사각형이 총 1개
n=3인 경우 정사각형이 총 6개
n=4인 경우 정사각형이 총 20개
n=5인 경우 정사각형이 총 50개
그러면 이제 여기서 눈치를 채면 사실 좋지
| n | 격자형 정사각형 | 기울어진 정사각형 | 전체 정사각형의 개수 |
| 2 | $1^2=1$ | 0 | 1 |
| 3 | $1^2+2^2=5$ | 1 | 6 |
| 4 | $1^2+2^2+3^2=14$ | 6 | 20 |
| 5 | $30$ | 20 | 50 |
| 6 | $55$ | x | y |
위 표를 보면 규칙을 예상할 수 있다
n=2인 경우 전체 정사각형의 개수는 n=3인 경우 기울어진 정사각형의 개수와 동일하다
.....
n=k인 경우 전체 정사각형의 개수는 n=k+1인 경우 기울어진 정사각형의 개수와 동일하다
근데 이건 너무 증거없이 예상하는것도 맞다고 생각함
그래서 n=6인 경우 기울어진 정사각형을 구해서 확인하는게 제일 베스트인데
n=5인 경우도 쉽게 계산이 안되는데 n=6은 말 다했지

실제로 위 그림을 보면 n=6인 경우 기울어진 정사각형의 개수는 50개
근데 결국에는 정답을 하나라도 맞추는게 중요하기 때문에 적은 증거로 규칙을 눈치채는것도 실력이라고 생각한다
규칙이 있을 것이라고 분명히 확신을 하고 시작을 하기 때문에
그래서 주어진 n에서 전체 정사각형의 개수는...
def solution(n):
answer = 0
n = n-1
def a(n):
return (n)*(n+1)*(2*n+1)//6
sum_b_n = []
for i in range(1,n):
sum_b_n.append(a(i))
answer = a(n)+sum(sum_b_n)
return answer
처음에 문제 풀때는 위와 같이 풀었다
격자형 정사각형의 개수는 명백해서 n = n-1로 두면 $1$, $1^2+2^2$, $1^2+2^2+3^2$,....$n^2$까지 더해서 구하면 될거고
기울어진 정사각형의 개수($b_{n}$)는 0,1,6,20,50,105,196,.....
계차수열($c_{n}$)을 구하면 1,5,14,30,55,91,....
한번 더 계차수열($d_{n}$)을 구하면 4,9,16,25,36,.....
$$d_{n} = c_{n+1}-c_{n} = (n+1)^2$$
$c_{n}$를 구하기 위해서 n=1부터 n까지 넣어서 전부 합하면..
$$c_{2}-c_{1} = 2^2$$
$$c_{3}-c_{2} = 3^2$$
$$c_{4}-c_{3} = 4^2$$
...
$$c_{n}-c_{n-1} = n^2$$
$$c_{n}-c_{1}= \sum_{k=1}^{n} (k+1)^2$$
$$c_{n} = 1 + \sum_{k=2}^{n-1} (k)^2 = \sum_{k=1}^{n-1} (k)^2 = grid square $$
$c_{n}$이 격자형 정사각형의 개수와 동일하다
그래서 기울어진 정사각형의 개수 $b_{n}$은
$$b_{2}-b_{1} = c_{1}$$
$$b_{3}-b_{2} = c_{2}$$
$$b_{4}-b_{3} = c_{3}$$
...
$$b_{n}-b_{n-1} = c_{n}$$
$$b_{n}-b_{1}= \sum_{k=1}^{n} c_{k}$$
$$b_{n}= \sum_{k=1}^{n} c_{k}$$
그래서 격자형 정사각형의 개수를 구하는 함수 a(n)을 정의하고
n=1부터 n까지 반복해서 a(n)의 값을 구해서 리스트에 저장한다음에 리스트의 총합 sum([a(n)])과 a(n)의 합을 정답으로
return
근데 이렇게 복잡하게 구했지만 결국에 따지고 보면 n=k인 경우 전체 정사각형의 개수는 n=k+1인 경우 기울어진 정사각형의 개수와 동일하다
라는 결론과 동일하다...
def solution(n):
answer = 0
n = n-1
def a(n):
return (n)*(n+1)*(2*n+1)//6
total_n = {0:0,1:1,2:6,3:20,4:50}
for i in range(1,n+1):
answer = a(i) + total_n[i-1]
total_n[i] = answer
return answer
격자형 정사각형의 개수를 세는 함수 a(n)을 정의하고
전체 정사각형의 개수는 n에 따라 total_n에 저장해둔 다음에
i=2부터 n까지 반복을 해서
현재 i에 대한 격자형 정사각형의 개수 + 이전 i-1에서의 전체 정사각형의 개수( = 현재 i에서의 기울어진 정사각형의 개수) = 현재 i에 대한 전체 정사각형의 개수
를 통해 answer를 갱신해 나간다
이 때 이전에 푼 문제는 total_n에 저장해서 재활용하는 방식으로 코딩
3. 되돌아보기
정답을 정확히 찾진 못했지만 규칙이 있겠구나 눈치채고 규칙성을 찾고자 한게 좋았다
이런 문제도 얼마든지 나올수 있기 때문에 유연하게 생각
4. 참고
https://tr.funmathfan.com/post/the-number-of-lattice-squares
The Number of Lattice Squares*
There are many puzzles about the number squares you can draw by using the grid points ( lattice points) on a given grid. Here is an example; The correct answer is not 9 (the number of 1x1 squares). There are many other squares you can create using the give
tr.funmathfan.com
'알고리즘 > 알고리즘 일반' 카테고리의 다른 글
| 탐욕법 활용 기초편 (0) | 2021.11.23 |
|---|---|
| 시간 다루기 (0) | 2021.11.22 |
| 문자열 다룰 때 필수적으로 갖춰야할 스킬들 (0) | 2021.11.21 |
| 완전히 탐색해야할때는.. (0) | 2021.11.21 |
| 반복문을 줄이는 방법 (0) | 2021.11.19 |

