1. 개요
수열이 계속 변화할때, 이 수열의 중앙값을 어떻게 빠르게 구할 수 있을까
매번 정렬해서 중간의 값을 찾아야하는가?
최대 힙과 최소 힙을 이용하면 중앙값을 아주 쉽게 찾을 수 있다
결론부터 말하자면, (크기와는 무관하게) 항의 순서대로 수열이 주어질때
최대힙에 들어간 원소의 수와 최소힙에 들어간 원소의 수가 서로 같을 때는 최대힙에 수를 넣어주고
최대힙의 원소의 수가 최소힙의 원소의 수보다 1개 더 많을때는 최소힙에 수를 넣어준다
즉 항상 최대힙 > 최소힙 > 최대힙 > 최소힙 >.. 으로 번갈아가면서 수를 넣어준다.
힙은 완벽하게 정렬해주지는 않지만, 루트에는 최소힙이면 힙에 들어간 원소들 중 최솟값이,
최대힙이면 힙에 들어간 원소들 중 최댓값이 온다는건 확실하다
최대힙에 원소를 넣으면 최대힙의 루트(0번째 원소)에는 항상 가장 큰 원소가 오고
최소힙에 원소를 넣으면 최소힙의 루트(0번째 원소)에는 항상 가장 작은 원소가 오게 된다
이때 최대힙의 0번째 원소는 최소힙의 0번째 원소보다 항상 작게 유지한다
즉, 최대힙의 0번째 원소가 최소힙의 0번째 원소보다 크다면, 서로 자리를 교환한다
그렇게 한다면 최대힙의 0번째 원소에는 항상 중앙값이 오게된다
그림으로 생각하면 명백하다
2. 그림으로 생각하는 알고리즘
1,5,2,10,8,7,5를 순서대로 말할때, 각 순서에서 중앙값이 어떻게 변하는지 알아보자
최초 최대힙과 최소힙의 원소의 수는 0개로 같으므로 최대힙에 수를 먼저 넣는다
중앙을 잘 보면.. 현재 수열에 1이 1개 있는 상태이다.. 그래서 중앙값은 1이다
다시 5를 넣어보자.. 이번엔 최대힙의 원소가 1개 더 많으므로 최소힙에 넣어준다

현재 상태에서 수열은 1,5로 되어있다.
심지어 아래에서 위로 읽으면 오름차순 정렬된거나 마찬가지다.
여기서 중앙값은? 정의하기에 따라 다르겠지만 둘 중 작은 값 1을 중앙값으로 하든가, 1과 5의 평균인 3으로 하든가
다음, 2를 넣어보자. 최대힙과 최소힙의 원소의 수가 동일하므로 최대힙에 넣어준다
이때, 최대힙에는 가장 큰 원소가 top으로 올라온다

아래에서 위로 읽어보자, 1,2,5로 정렬된 상태이다. 그렇다면 중앙값은? 최대힙의 가장 위인 2가 된다
다시 10을 넣어보자. 최소힙의 원소 수가 1 적으므로, 최소힙에 넣어준다.
이때, 최소힙에서 가장 작은 원소가 최소힙의 맨 위로 올라온다

아래에서 위로 읽어보면 1,2,5,10으로 정렬된 상태이다.
중앙값은? 최대힙의 맨 위 원소와 최소힙의 맨 위 원소 2와 5중 작은 값으로 하든가, 평균으로 하든가.. 정의하기에 따라 다르다
이번엔 8을 넣는다. 최대힙과 최소힙의 원소 수가 동일하므로 최대힙에 넣어준다
그리고 최대힙의 맨 위에는 가장 큰 원소가 올라온다..(다른 원소들의 정렬 상태는 적당히 된다고 가정)

아래에서 위로 읽어보면 1,2,8,5,10,...으로 되어있다
물론 힙은 오직 루트의 원소만 최댓값이거나 최솟값임을 확실히 보장할 수 있고 (실제로 -99,1,2,5,10, 이렇게 되어 있는지는 해봐야 안다..)
아무튼 중앙값을 구하는게 목표인데 현재 최대힙의 top의 원소가 최소힙의 top의 원소보다 크다.
그래서 최대힙의 top과 최소힙의 top을 서로 자리를 교환한다

이것으로 알 수 있는 것은 최대힙의 모든 원소들은 최소힙의 모든 원소들보다 작게 유지해야한다는 것이다.
그래야 최대힙의 top에 항상 수열의 중앙값이 오게 된다..
다시 말하지만 최대힙과 최소힙의 top에만 어떤 수가 올지 확실히 알 수 있다
그러니까 실제로는 2,1,5,8,10으로 되어 있을 수도 있다는 것인데,
중앙값을 구하는게 목표라서.. 2,1,5,8,10되어있다고 하더라도, 5와 8의 위치는 확실하게 알 수 있어서 5가 중앙값이라는 것은 확실하게 알 수 있다
다음으로 7을 넣어보자
이번엔 최소힙의 원소 수가 최대힙보다 1개 적으므로 최소힙에 넣어준다
그러면 최소힙에서 가장 작은 원소인 7이 top으로 올라오게 된다

이러면 아래에서 위로 보면 1,2,5,7,8,10으로 되어있다.. 중앙값은? 최대힙의 top인 5와 최소힙의 top인 7중에서 더 작은 5로 하든가, 아니면 둘의 평균 6으로 하든가..
마지막으로 5를 넣어보자. 최대힙과 최소힙의 원소 수가 동일하므로 최대힙에 넣어준다.
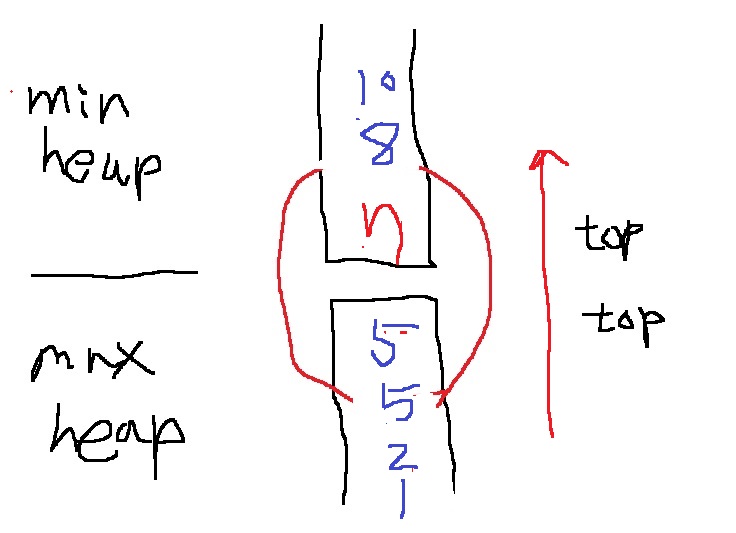
그러면 1,2,5,5,7,8,10으로 되어있다.. 중앙값은? 최대힙의 top인 5가 된다.
3. running median
수열이 변화할때, 2개의 우선순위 큐로 중앙값을 빠르게 찾고자 하는 알고리즘이다.
수열이 차례대로 a1,a2,a3,...로 주어질때,
3-1) 최대힙의 원소의 수와 최소힙의 원소의 수가 동일하면, 최대힙에 수열의 원소를 넣는다
3-2) 최대힙의 원소의 수가 최소힙의 원소의 수보다 1개 더 많으면, 최소힙에 수열의 원소를 넣는다.
3-3) 최대힙의 0번째 원소가 최소힙의 0번째 원소보다 크다면, 서로 자리를 교환한다
3-4) 그럴때, 힙에 들어간 원소의 수가 홀수개이면 최대힙의 top에 중앙값이 존재하고 짝수개이면 중앙값을 정의하기에 따라 다르지만 최대힙의 top과 최소힙의 top중에서 더 작은 값은 최대힙의 top에 있다.
4. 연습문제
1655번: 가운데를 말해요
첫째 줄에는 백준이가 외치는 정수의 개수 N이 주어진다. N은 1보다 크거나 같고, 100,000보다 작거나 같은 자연수이다. 그 다음 N줄에 걸쳐서 백준이가 외치는 정수가 차례대로 주어진다. 정수는 -1
www.acmicpc.net
수열이 차례대로 주어질때, 각 차례에서 현재 존재하는 수열의 중앙값을 구하는 문제
5. 구현 예시
위의 running median 알고리즘을 그대로 구현하면 된다
최대힙과 최소힙의 크기가 동일하면, 최대힙에 원소를 넣고
최대힙의 원소 수가 최소힙의 원소 수보다 1개 더 많으면 최소힙에 원소를 넣는다
최대힙에 원소를 넣을때는 (-실제원소,실제원소)로 넣어줘야 최대힙이 만들어진다
그리고 최대힙과 최소힙에 모두 원소가 존재할때,
최대힙의 top이 최소힙의 top보다 더 크다면, 서로 자리를 교환한다
단순히 인덱스 교환하면 heap으로 생각을 안하나봐.. 틀렸다고 나오네?
교환할때는 heappop으로 원소를 빼주고,
다시 heappush로 서로 최대힙거는 최소힙에 최소힙거는 최대힙에 넣어주면 교환이 될거임
그러면 매 차례에 최대힙의 top에 중앙값이 존재하게 된다
import heapq
from sys import stdin
min_q = [] #최소힙
min_len = 0 #최소힙의 크기
max_q = [] #최대힙
max_len = 0 #최대힙의 크기
n = int(stdin.readline())
for _ in range(n):
##현재 들어오는 수열의 값
x = int(stdin.readline())
#최대힙의 원소 수와 최소힙의 원소 수가 동일하면
if max_len == min_len:
#최대힙에 수열의 원소를 삽입
#최대힙에는 (-실제원소,실제원소)로 넣어준다
heapq.heappush(max_q,(-x,x))
max_len += 1 #삽입했으니 최대힙 크기를 1 증가
#최대힙의 원소 수가 최소힙의 원소 수보다 1 더 크면
elif max_len == min_len+1:
#최소힙에 수열의 원소를 삽입
heapq.heappush(min_q,x)
min_len += 1 #원소를 넣었으니 최소힙 크기 1 증가
##최대힙과 최소힙에 모두 원소가 존재할때,
if max_len >= 1 and min_len >= 1:
##최대힙의 top이 최소힙의 top보다 크다면
if max_q[0][1] > min_q[0]:
a,b = heapq.heappop(max_q)
c = heapq.heappop(min_q)
##최대힙의 top과 최소힙의 top을 서로 교환
##당연하지만 heappop을 하고 heappush로 해서 넣어줘야지
##인덱스 교환하면 안돼..
##아니 해도 되나?? 모르겠네
heapq.heappush(max_q,(-c,c))
heapq.heappush(min_q,b)
##매 차례에 중앙값은 최대힙의 top에 존재한다
print(max_q[0][1])'알고리즘 > 자료구조(스택,큐,해시맵)' 카테고리의 다른 글
| [Java]running median 복습하면서 자바로 구현해보기 (0) | 2023.03.21 |
|---|---|
| [Java]자바 우선순위 큐 응용하기1 -뒤에서부터 생각하면 효과적으로 변하는 경우- (0) | 2023.03.20 |
| 우선순위 큐 재활하면서 응용력 키우기1 -카드 정렬하기, N번째 큰 수 (0) | 2023.03.18 |
| 스택 테크닉 익히기1 -문자열 폭발 (0) | 2023.01.29 |
| stack 활용법 - 올바른 괄호 문자열 판별 (0) | 2021.11.17 |

