1. 문제
https://www.acmicpc.net/problem/10816
10816번: 숫자 카드 2
첫째 줄에 상근이가 가지고 있는 숫자 카드의 개수 N(1 ≤ N ≤ 500,000)이 주어진다. 둘째 줄에는 숫자 카드에 적혀있는 정수가 주어진다. 숫자 카드에 적혀있는 수는 -10,000,000보다 크거나 같고, 10,
www.acmicpc.net
주어진 수열에서 특정한 수들이 몇개나 있는지 찾는 문제
2. lower bound와 upper bound
지금까지 배웠던 이진탐색 알고리즘은 특정한 수가 존재하는지, 존재하지 않는지만 알아보는 알고리즘이다.
하지만 수열에서 특정한 수가 여러개 존재할 수도 있는데 그럴때 이진탐색으로 몇개나 존재하는지 알 수 있을까
만약 특정한 수가 가장 먼저 나오기 시작하는 위치와, 가장 나중에 나오는 위치를 알 수 있다면?
그것을 찾아주는 알고리즘이 lower bound와 upper bound이다
이진탐색에서는 특정 수를 찾는 순간 그 위치를 바로 return했는데, lower bound와 upper bound는 특정 수를 찾더라도 return하지 않으면 된다
def binary_search(array, target, start, end):
while start <= end:
mid = (start + end)//2
##########################
if array[mid] == target:
return array[mid]
###################### 여기를 제거
elif array[mid] > target:
end = mid-1
else:
start = mid+1
return None
중간에 if array[mid] == target: return array[mid]를 제거하고 계속해서 탐색을 수행함
이진탐색에서는 array의 길이가 n이면 start = 0, end = n-1로 탐색을 수행했지만
lower bound, upper bound에서는 길이가 n이면 start = 0, end = n으로 탐색을 수행함
이유는 나중에 알 수 있다
그림으로 먼저 생각해보자
2,3,4,5,5,6,7,7,7에서 7이 가장 먼저 나오는 위치를 찾고 싶다
start = 0, end = 9로 하고 이진 탐색을 수행하자
mid = 4가 가리키는 위치는 5인데, 이때 어떻게 움직여야 7을 찾을 수 있을까
start를 mid+1로 움직이면 7을 향해 갈 것이다
즉 target > array[mid]이면, start를 mid+1로 움직인다
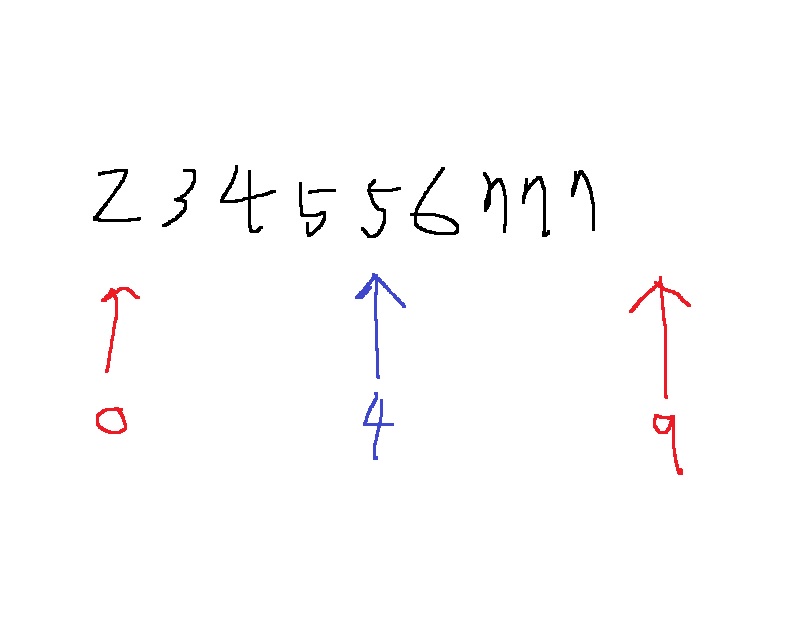
그러면 5~9에서 7이 가장 먼저 나오는 위치를 찾고 싶다
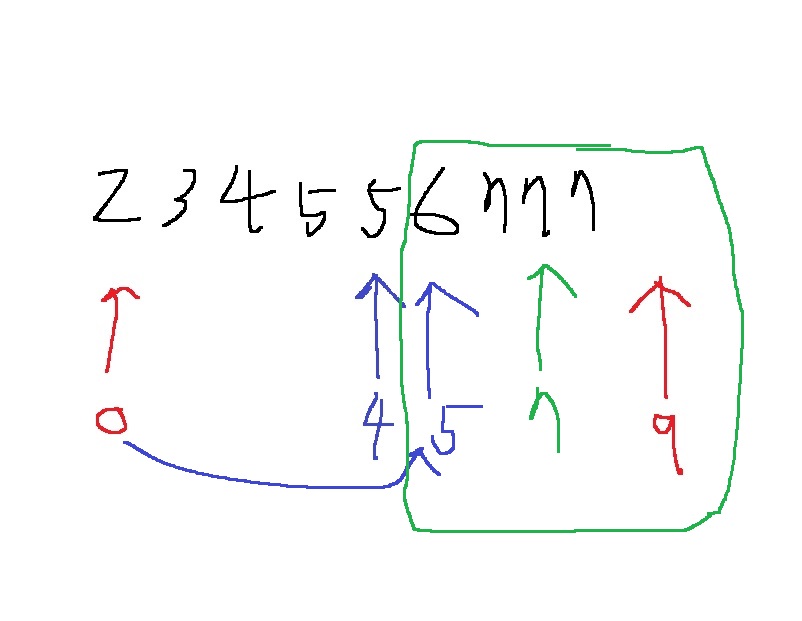
위와 같이 mid가 7인데 이럴때, 가장 먼저 나오는 7은 어떻게해야 찾을 수 있을까??
end를 mid로 옮겨?? mid-1로 옮겨??
당연히 mid로 옮겨야한다.
mid-1로 옮기는건 위험한게 mid가 처음으로 나오는 위치일수도 있거든
그래서 target <= array[mid]이면 end = mid로 옮기면 된다
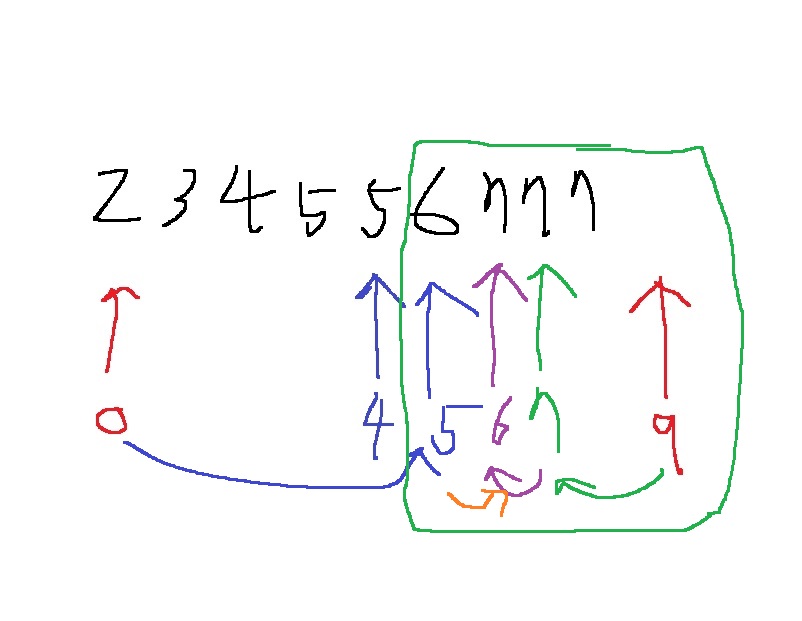
위에서 정한 룰대로 target <= array[mid]이면 end = mid로 옮기고 target > array[mid]이면 start = mid+1로 옮기다보면
위와 같이 start = end인 6에서 끝나게 된다
저기가 바로 7이 최초로 나오는 위치이다
그러면 반복문이 끝나고 start나 end를 return하면 되는데
근데 이럴때 end를 return해야하나 start를 return해야하나..?
당연히 end를 return해야한다
end = mid, start = mid+1이므로, mid에서 target이 찾아지는데, start > end일 수 있기때문에 start를 return하면 정확한 위치를 못찾을 수 있다
(그런 경우가 있나?? 다시 해보니까 없는것 같기도 하고)
def lower_bound(array,target):
n = len(array)
start,end = 0,n
while start < end:
mid = (start+end)//2
if target <= array[mid]:
end = mid
else:
start = mid + 1
if end == n:
return -1
else:
if array[end] == target:
return end
else:
return -1
그리고 end = n으로 시작하는 이유는, 만약에 수열에서 원하는 target을 찾지 못할 수가 있다
그런 경우에 end = n으로 변화가 없는데, end = n이면 찾지 못했다는 뜻으로 받아들이면 된다
end=n은 인덱스로 존재하지 않기때문에 바로 확인가능한데
물론 end = 0으로 끝날수도 있다.
그런 경우에 0번 값을 확인해보고 target과 다르다면 찾지 못했다고 판단할 수 있다
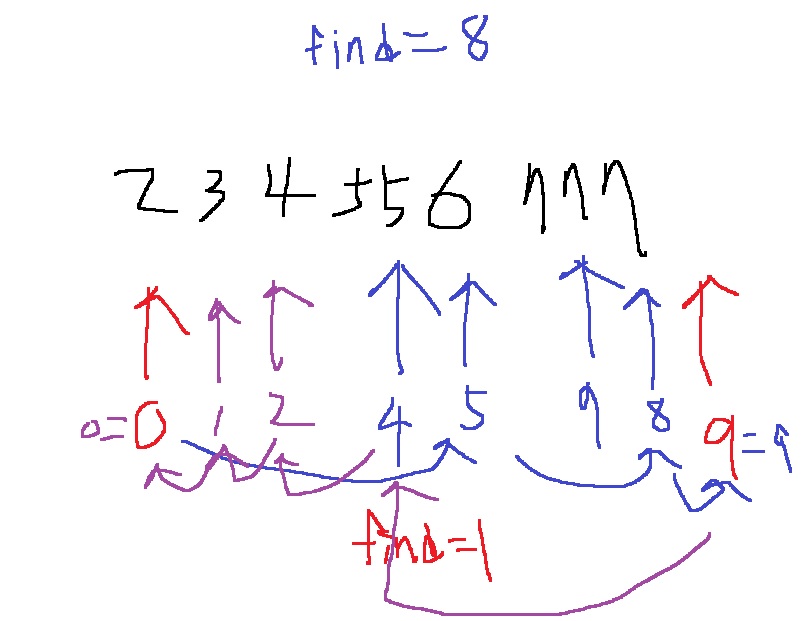
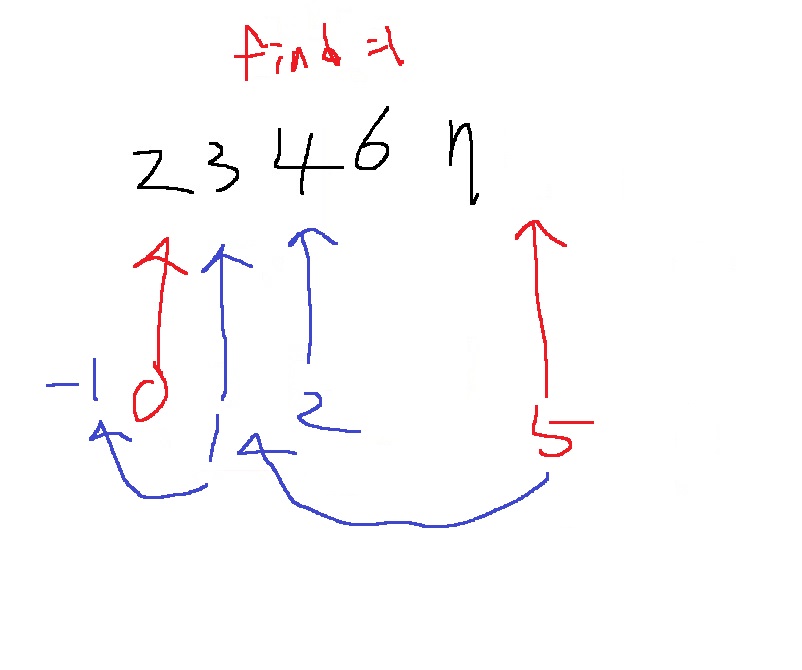
위 그림에서 보듯이 1과 8을 찾을때 각각 start와 end 인덱스로 이동함
그리고 중간에서 값을 찾지 못할수도 있는데
예를 들어 2,3,4,6,7,7,7에서 5를 찾고 싶다면.. start = end = 3이지만 거기는 6이다

다음으로 upper bound는 어떻게 찾을까
2,3,4,5,5,6,6,7,7,7에서 5가 마지막에 나오는 위치를 찾고 싶다
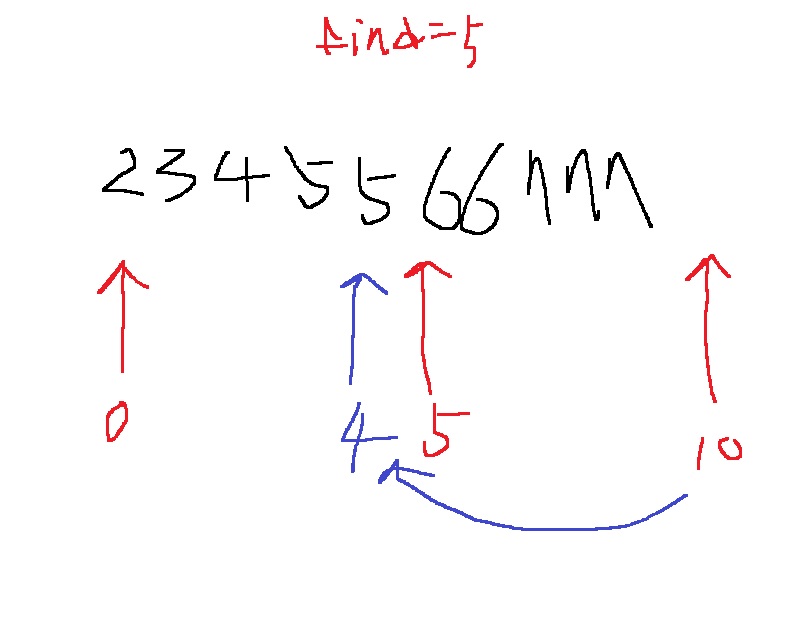
위와 같은 경우 target < array[mid]이면 end를 mid-1로 옮기면 될 것이다
어차피 array[mid]와 target은 다르니까 mid 위치 값은 볼 필요도 없다
계속해서 mid=2이고 target >= array[mid]이면 start를 mid로 옮기면 될 것이다

마찬가지로 2~4이면, mid=3이고 target >= array[mid]이므로 start = mid로 옮긴다
그리고 3~4이면 mid=3이고 target >= array[mid]이므로.. start = mid로 옮긴다..?
근데 이러면 무한 루프네
아하 start는 mid+1로 옮기는게 무조건 맞다
근데 end = mid로 옮겨야 하는 이유를 찾았어
반례가 있네
end = mid-1로 해버리면 다음과 같은 경우에 2,3,4,5,5,6,7,7,7에서 6을 찾고 싶은데

최종 위치가 end = 6이 되어버려.. 실제 6은 end=5에 있는데
그래서 end = mid-1로 하면 end-1이 실제 위치인 경우가 있고 end가 실제 위치인 경우가 생긴다
하지만 end = mid로 하면 모든 경우에 end-1이 실제 위치가 된다
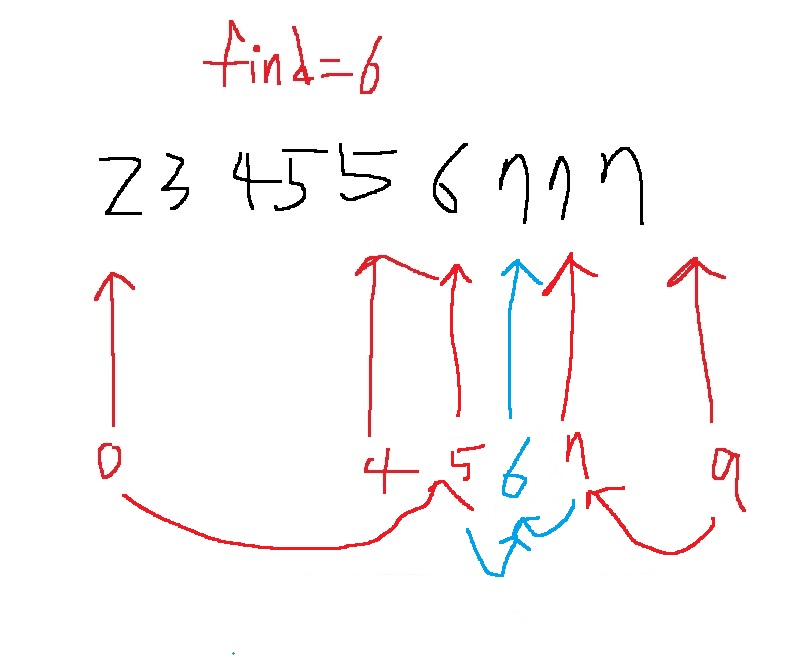
최종위치 6, 실제 위치는 6-1인 5

최종 위치 5, 실제 위치는 5-1=4
def upper_bound(array,target):
n = len(array)
start,end = 0,len(array)
while start < end:
mid = (start+end)//2
if target < array[mid]:
end = mid
else:
start = mid + 1
if end < 0:
return -1
else:
if array[end-1] == target:
return end-1
else:
return -1
예외가 있을까??? 첫부분, 중간부분, 마지막부분에서 좀 생각해보면
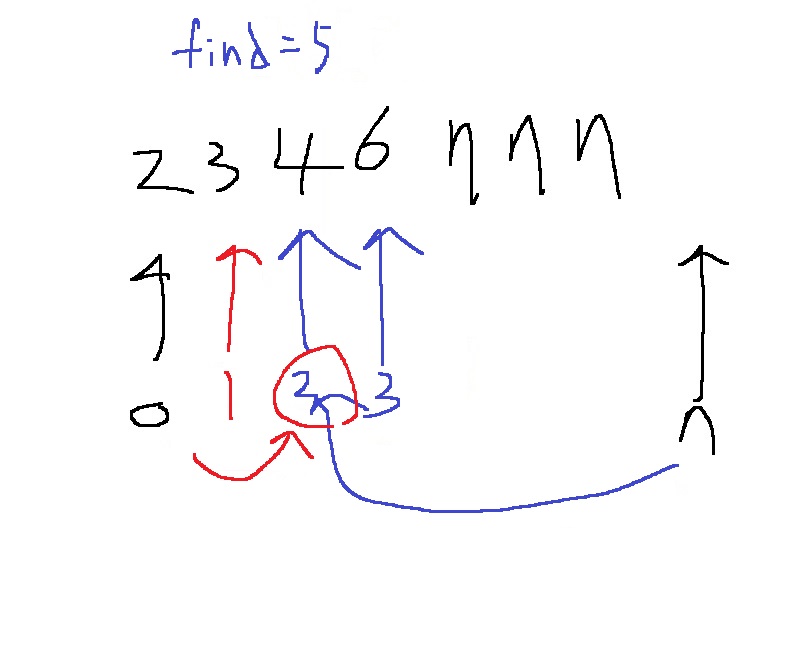
중간에서 찾지 못하면 end를 정상 반환해도 array값과 비교해봐야겠는걸
그리고 마지막 7의 위치를 찾고 싶다면
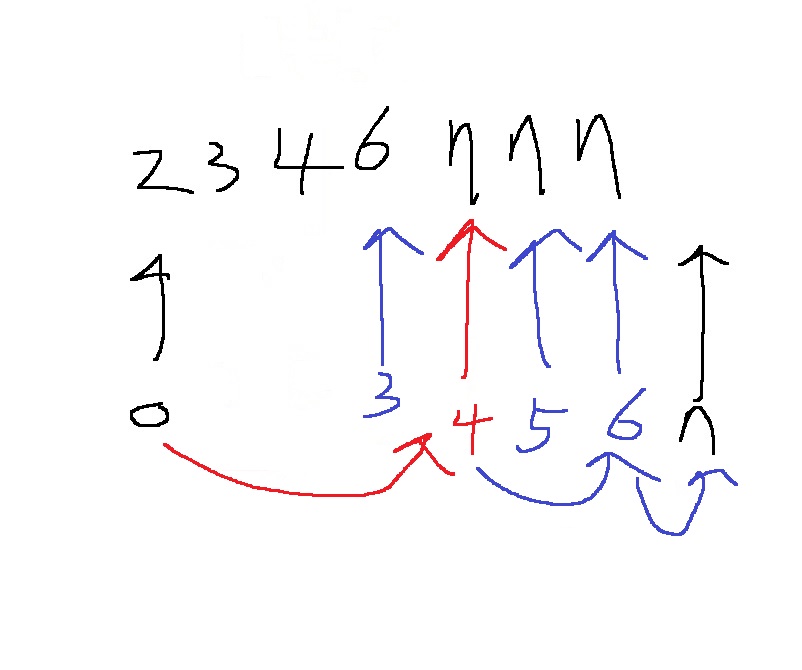
정확히 찾더라도 start = mid+1때문에 end = n으로 이동을 한단 말이지
end-1이 target과 같은지 비교해봐야겠는걸
매우 작은 수를 찾고자 한다면??
-1이나 0이 될 수 있단 말이야
3. 되돌아보기..
근데 내가 생각하기에 lower_bound랑 upper_bound는 수가 존재한다고 확실히 보장할 수 있다면 쓰는게 좋겠다
뭔가 생각 못한 경우의 수가 더 있을 것 같은데??
근데 일단 문제는 맞춘것 같다
4. 풀이
lower bound와 upper bound 함수를 구현하고, lower bound에서 -1을 얻으면 존재하지 않는다는 뜻이므로 바로 0을 ans_list에 append하고
-1이 아니라면, upper_bound도 구해본다음에
(upper)-(lower)+1이 개수라는 점을 생각하면 된다
from sys import stdin
def lower_bound(array,target,start,end):
while start < end:
mid = (start+end)//2
if target <= array[mid]:
end = mid
else:
start = mid + 1
if end == len(array):
return -1
else:
if array[end] == target:
return end
else:
return -1
def upper_bound(array,target,start,end):
while start < end:
mid = (start+end)//2
if target < array[mid]:
end = mid
else:
start = mid + 1
if end < 0:
return -1
else:
if array[end-1] == target:
return end-1
else:
return -1
n = int(stdin.readline())
num_list = list(map(int,stdin.readline().split()))
m = int(stdin.readline())
target_list = list(map(int,stdin.readline().split()))
num_list.sort()
ans_list = []
for target in target_list:
a = lower_bound(num_list,target,0,n)
if a == -1:
ans_list.append(0)
else:
b = upper_bound(num_list,target,0,n)
ans_list.append(b-a+1)
print(*ans_list)
'알고리즘 > 이분 탐색' 카테고리의 다른 글
| 이분탐색 응용력 키우기 연습1 -차이가 가장 가까운 값을 찾는 방법- (0) | 2023.03.28 |
|---|---|
| 이분탐색을 이용해서 MN개의 조합에서 k번째 수를 찾는 놀라운 방법 (0) | 2023.03.21 |
| 이진 탐색 정복 -array를 쓰지 않아도 되는 경우- (0) | 2022.09.18 |
| 이진 탐색 정복기2 - 이진 탐색이란..- (0) | 2022.09.10 |
| 이진 탐색 정복기1 -기본 이론 순차 탐색?- (0) | 2022.09.08 |

