2022/08/15
1. abstract
long term time series forecasting(LTSF)에 대해 transformer 기반의 해결책들이 최근에 많이 뜨고 있다.
과거 몇년간 성능이 증가하고 있음에도 불구하고 이 주제에서 이런 연구의 유효성에 대해 의문을 품고 있었다.
특히 transformer가 틀림없이 긴 sequence에서 원소들 사이에 의미적인 연관관계를 추출하는데 가장 성공한 solution이라는 것은 분명하다.
그러나 time series 모델링에서 우리는 연속적이면서 순서를 가진 점의 집합에서 시간적인 관계를 추출해야한다.
positional encoding과 transformer의 부분 수열에 token을 쓰는 것이 어느정도 순서적인 정보를 보유하는데 도움을 주지만
순열 불변의 self attention 메커니즘의 본성이 불가피하게 시간적인 정보의 손실을 낳는다
우리 주장의 정당성을 입증하기 위해 우리는 비교를 위해 단순한 1층 layer의 집합 모델인 LTSF-linear 모델을 소개한다.
9개의 현실 데이터셋에 대해서 실험 결과는 LTSF-linear 모델이 놀랍게도 복잡한 transformer 기반의 LTSF 모델의 성능을 모든 경우에, 종종 큰 격차로 뛰어 넘는다는 것을 보여주고 있다.
게다가 우리는 LTSF 모델의 시간적 관계를 추출하는 능력에 대해 포괄적인 경험적 실험을 수행했다.
우리는 이러한 놀라운 발견이 LTSF task에서 새로운 실험 방향을 열어줄 것을 희망한다.
우리는 또한 transformer 기반의 해결책의 유효성을 미래에 anomaly detection 같은 다른 time series 분석에 재검토해보기를 원한다.
지금 현재 1등인 엄청난 모델이라는데 단순한 linear model이라고?
2. introduction
time series는 오늘날 데이터가 넘치는 세상에서 어디에나 있다.
주어진 역사적 데이터에서 time series forecasting은 교통량 예측, 에너지 관리, 경제 투자 이외에도 다양한 응용에 적용되는 역사가 긴 task이다.
과거 수십년간에 TSF solution은 전통적인 통계모델 ARIMA, 머신러닝 테크닉 GBRT에서 딥러닝 기반의 RNN과 Temporal Convolutional network로 변해왔다.
transformer은 가장 성공적인 sequence modeling architecture라는 것은 틀림없으며 다양한 응용, 예를 들어 NLP, speech recognition, computer vision에서 견줄데가 없는 성능을 보여주었다.
최근에 time series analysis에 transformer 기반의 해결책들이 엄청 나타나고 있다.
대부분 주목할만한 모델들은 덜 연구되었고, 도전할만한 long term time series forecasting인 LTSF 문제에 주목하고 있고 LogTrans, Informer, Autoformer, Pyraformer, Triformer, 최근 FEDformer등이 있다.
transformer의 주된 파워는 multi head self attention 메커니즘에 있고 image의 2d patch나 text사이 word들의 long sequence에서의 원소들 사이의 의미적 관계를 추출하는데 놀랄만한 능력을 보여준다.
그러나 self attention은 순열 불변(permutation invariant)이면서 어느정도는 순서에 반한다(anti-order)
다양한 타입의 positional encoding 테크닉들이 어느정도 순서 정보를 보존할 수 있지만, 그들의 상위에서 self attention을 적용하고 나서는 시간적 정보의 손실이 여전히 불가피하다.
이것은 보통 NLP같은 의미적인 정보가 풍부한 경우에서는 심각한 문제는 아니다. 우리가 단어 순서를 바꾸더라도 문장의 의미적 정보가 어느정도 보존된다.
그러나 time series data를 분석할 때 종종 수치적 데이터 그 자체에서 의미적 정보의 부족이 있어서
우리는 주로 연속적인 포인트 집합에서 시간적 변화를 모델링하는 것에 관심이 있다.
다시 말해 순서 그 자체가 주된 핵심 역할이라는 것이다. 결과적으로 우리는 다음과 같은 흥미로운 질문을 할 수 있다
transformer이 정말로 long term time series 예측에 효과적인가? (Are Transformers really effective for long-term time series forecasting?)
게다가 현재 존재하는 transformer 기반의 LTSF 솔루션이 전통적인 방식에 비해 상당한 예측 정확도 개선을 보여준다.
그들 실험에서는 모든 비교군(non-transformer) 베이스라인이 autoregressive나 iterated multi-step 예측을 수행했다.
이들은 LTSF 문제에서 상당한 에러 누적 효과를 가지고 있다.
그러므로 이 논문에서는 우리는 direct multi-step 예측 전략을 가지는 transformer 기반의 LTSF 솔루션이 실제 성능에 유효한지를 알고 싶다.
비교군이 애초에 안좋았으니까 성능이 좋아보였지, 실제로 좋다고 생각할 수는 없다.. 이런말인듯?
카오스 시스템같은 long term forecasting은 고사하고 모든 time series가 예측 가능한 것은 아니다.
우리는 time series가 분명하게 트렌드를 가지고 있고 주기성을 가지고 있으면서 time series forecasting이 실현 가능하다라고 가정했다.
linear model이 이미 그러한 정보를 추출할 수 있기 때문에 우리는 당혹스럽게도 LTSF-Linear 이라는 새로운 비교군으로 단순한 모델을 소개한다.
LTSF-Linear은 미래의 time series를 직접적으로 예측하기 위해 1층 linear model로 time series를 회귀분석한다.
우리는 9개의 널리 사용되는 benchmark에 대해 광범위한 실험을 수행했고, 이들은 다양한 현실 응용으로 traffic, energy, economics, weather, disease prediction을 포함한다.
놀랍게도 우리의 결과는 LTSF-Linear이 현존하는 복잡한 transformer 기반의 모든 케이스의 모델들의 성능을 뛰어 넘고 있고 종종 큰 격차(20%~50%)정도 뛰어넘는다
게다가 우리는 현존하는 transformer에 대한 주장과는 다르게 그들의 대부분이 long sequence에 대해서 시간적인 정보를 추출하지 못한다는 것을 발견했다.
다시 말해 예측 오차가 look back window size의 증가에 따라 감소하지 않는다. 종종 증가하는 경우도 있다는 말이다.
마지막으로 우리는 현존하는 transformer기반의 TSF solution에 대해 ablation study를 수행하여 그들의 다양한 디자인의 효과를 실험해보았다.
요약하자면 이 논문의 기여점은
2-1) 우리의 최선의 지식 하에서 이것은 long term time series forecasting에 대해 transformer의 효과에 도전한 첫 논문이다.
2-2) 우리 주장을 증명하기 위해 우리는 단순한 1층 선형 모델, LTSF-Linear이라는 이름을 가진 모델을 소개하고
그들을 현재 존재하는 transformer 기반의 LTSF solution과 9개의 benchmark에 대해 비교했다.
LTSF-linear은 LTSF 문제의 그 자체로 새로운 베이스라인이 될 수 있다.
2-3) 우리는 포괄적인 경험적 연구를 다양한 분야의 transformer 기반의 솔루션에 수행하여 long input을 모델링하는 능력, time series 순서의 민감성, positional encoding, sub series embedding의 영향, 효과적인 비교에 대해 알아보았다.
우리의 연구 결과가 미래에 이 분야에 분명히 도움이 될 것이라고 생각한다.
위에서 보이듯이 우리는 transformer의 시간적인 모델링 능력이 적어도 현재 존재하는 LTSF 벤치마크에 대해서는 과장되어 있다라고 결론지었다.
동시에 LTSF-Linear 모델이 현존하는 모델에 비해 더 나은 예측 정확도를 보여서 LTSF 문제에 도전하는 몇 안되는 단순한 베이스라인으로 작용할 수 있다.
우리의 발견으로 미래에 다른 종류의 time series 분석에 대해 transformer기반의 방법의 유효성을 재검토해볼 필요가 있다고 생각한다.
3. preliminaries: TSF problem formulation
C개의 변량을 가지는 time series가 주어진 데이터 $X=\{ X^{t}_{1},...,X^{t}_{C}\}^{L}_{t=1}$에서 L이 window size이고
X^{i}_{t}는 i번째 변량의 t번째 time step이다.
time series forecasting task는 $\hat{X}=\{ \hat{X}^{t}_{1},...,\hat{X}^{t}_{C}\}^{L+T}_{t=L+1}$을 예측하는 것이다.
T > 1에서 iterated multi step forecasting은 single step forecaster를 배우고 반복적으로 multi step prediction을 얻기 위해 그것을 적용한다.
교대로 direct multi step forecasting은 직접적으로 multi step forecasting objective를 한번에 예측하는 것이다.
DMS forecasting 결과와 비교해서 IMS prediction이 autoregressive estimation 예측때문에 더 적은 분산을 가지고 있지만 그들은 불가피하게 error 누적 효과가 있다.
그 결과로 IMS forecasting은 더 높은 정확도를 가지는 single step forecaster가 있고 T가 상대적으로 적을때 선호될만하다.
대조적으로 DMS forecasting은 T가 크거나 unbiased single step forecasting model을 얻기 어려울 때 더 정확한 예측을 얻을 수 있다.
4. transformer-based LTSF solution
transformer 기반의 model들이 multihead self attention 메커니즘의 효과덕분에 많은 NLP와 computer vision task에서 비교할 수 없는 놀라운 성능을 보여주고 있다.
이것은 또한 transformer 기반의 time series 모델링 테크닉에 흥미로운 연구들을 유발시키고 있다.
특히 많은 연구들이 LTSF task에 전념하고 있다. transformer model들의 long range dependency를 포착하는 능력을 고려하여 대부분이 덜 연구되고 있는 long term forecasting problem에 집중하고 있다?
보통의 transformer model을 LTSF 문제에 적용해볼때, 원래 self attention 메커니즘의 quadratic 시간, 메모리 복잡도를 포함한 여러 제한점이 있고, autoregressive decoder 설계때문에 에러 누적효과가 있다.
Informer은 이러한 이슈를 다루고 감소된 복잡도를 가지는 새로운 transformer 아키텍처를 제안했고, DMS forecasting 전략을 사용했다.
후에 더 많은 transformer의 변형들이 다양한 모델의 성능, 효율성 개선을 위한 time series feature를 도입했다.
우리는 그림1에 현존하는 transformer 기반의 LTSF solution의 디자인들을 요약했다.
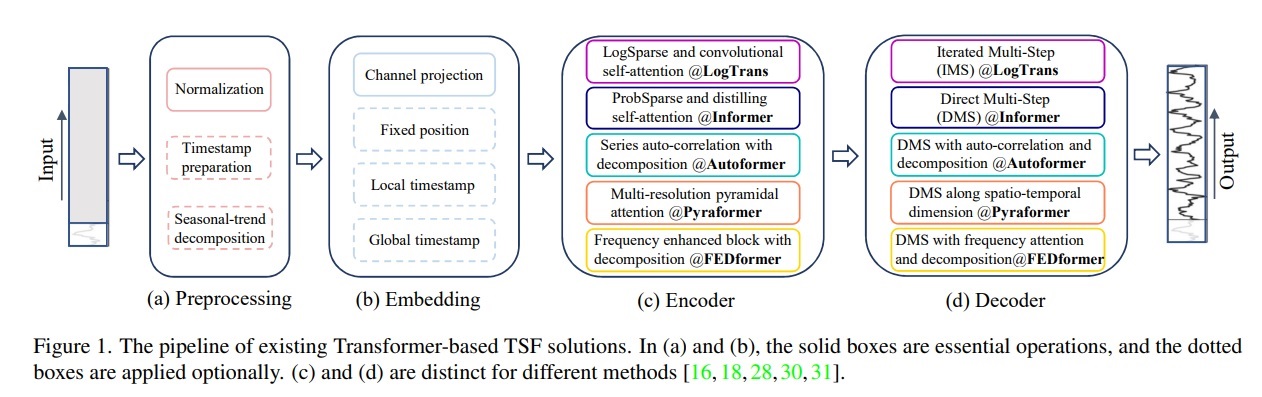
4-1) time series decomposition
데이터 전처리에서 zero mean으로 normalization하는 것이 TSF에서 공통적이다.
게다가 autoformer은 가장 먼저 seasonal trend decomposition을 각 neural block에 적용하여 raw data를 더 잘 예측할 수 있도록 time series 분석에서의 standard한 방법을 만들어냈다
특히 그들은 input sequence에서 moving average kernel을 사용하여 time series의 cyclical trend component를 추출해냈다
원래 sequence와 trend component의 차이는 seasonal component로 간주되느냐이다.
Autoformer의 decomposition 방식 위에 FEDformer은 expert 전략의 mixture를 제안하여 다양한 kernel size로부터 moving average kernel에 의해 추출된 trend component를 혼합시켰다.
4-2) input embedding strategies
transformer 아키텍처에서 self attention layer가 time series의 positional information을 보존할 수 없다.
그러나 local positional information, 즉 time series의 순서는 중요하다.
게다가 global한 시간적 정보 예를 들어 week, month, year과 holiday event같은 것도 또한 정보를 담고 있다.
time series의 시간적 문맥을 높이기 위해 SOTA transformer 기반의 방식의 실용적인 디자인은 몇가지 embedding을 주입하는 것이다.
예를 들어 fixed positional embedding, channel projection embedding, learnable temporal embedding
게다가 temporal convolutional layer?? 이런것도 있어??에서 temporal embedding과 learnable timestamp도 소개되었다.
4-3) self-attention scheme
transformer들은 self attention 메커니즘에 의존하여 pair된 원소들 사이 semantic dependency를 추출한다.
원래 transformer의 $O(L^{2})$ 시간, 메모리 복잡도를 줄이는데 영감을 받아 최근 연구들이 효율성을 위한 두가지 전략을 제안했다.
LogTrans와 Pyraformer은 self attention에 sparsity bias를 넣는다. 특히 LogTrans는 Logsparse mask를 사용하여 계산복잡도를 O(LlogL)로 줄였고
Pyraformer은 pyramidal attention을 적용하여 O(L)만에 계층적인 다양한 스케일의 temporal dependency를 포착했다.
다른 한편으로는 Informer와 FEDformer은 self attention matrix에서 low rank 속성을 사용한다.
Informer은 ProbSparse self attention 메커니즘과 O(LlogL)로 계산복잡도를 줄이기 위한 self attention distilling 연산을 사용하였다.
FEDformer은 O(L)복잡도를 얻기 위해 Fourier enhanced block과 wavelet enhanced block을 디자인하여 random 으로 선택했다
최근에 Autoformer은 원래 self attention layer를 대체하기 위해 series wise auto correlation을 디자인하였다.
4-4) Decoder
원래 transformer decoder은 autoregressive 방식으로 sequence를 내서 특히 long term prediction에서 inference speed를 줄이고 error 누적 효과를 낸다.
Informer은 DMS forecasting을 위해 generative style의 decoder를 디자인하였다.
다른 transformer 변형은 비슷한 DMS 전략을 냈다.
예를 들어 Pyraformer은 decoder로서 Spatio temporal axes를 fully connected layer에 concatentation하였다.
Autoformer은 trend cyclical component로부터 얻은 2개의 잘 정제된 decomposed feature를 합쳤고 seasnonal component를 위해 stacked auto correlation 메커니즘을 사용하여 마지막 prediction을 사용하였다.
FEDformer은 decomposition을 사용하여 마지막 결과를 decoding하기 위해 frequency attention block을 사용하여 decomposition을 수행했다.
transformer model의 전제는 pair된 원소 사이의 semantic correlation이다. 그렇지만 self attention이 순열 불변(permutation invariant)이고 그것의 시간적 관계를 모델링하는 능력이 전적으로 input token들 사이의 positional encoding에 의존한다.
time series의 raw numerical data를 고려하면(예를 들어 주가, 전기값) 그들 사이에 semantic한 관계는 찾기 어렵다.
time series modeling에서 우리는 paired 관계 대신에 원소들 사이의 순서, 연속된 점의 집합 사이에 시간적 관계가 주된 핵심 역할이다.
positional encoding과 sub series embedding은 어느정도 순서 정보를 보존하지만, 순열 불변의 self attention이 불가피하게 시간적 정보 손실을 낳는다
위의 관찰덕분에 우리는 transformer 기반의 LTSF 솔루션의 효과에 대해 재검토하는 것에 흥미를 가지게 되었다.
5. an embarrassingly simple baseline
현존하는 transformer 기반의 LTSF 솔루션의 실험에서 모든 non-transformer로 비교되는 비교군들이 IMS forecasting 테크닉을 사용하였는데, 이 테크닉은 상당한 에러 누적 효과를 보인다는 것으로 알려져있다.
우리는 그들에 DMS 전략을 사용하면 상당한 성능향상이 있을 것이라고 가정했다.
이런 가설을 입증하기 위해 우리는 가장 단순한 DMS 모델로 LTSF-Linear로 이름 붙인 temporal linear layer를 제안하고 비교를 위한 베이스라인으로 사용하고자 한다.
LTSF-linear의 기본 formulation은 직접적으로 미래 예측을 위한 time series를 가중합 연산을 이용해 regression한다.
아래 그림이 이를 보여준다
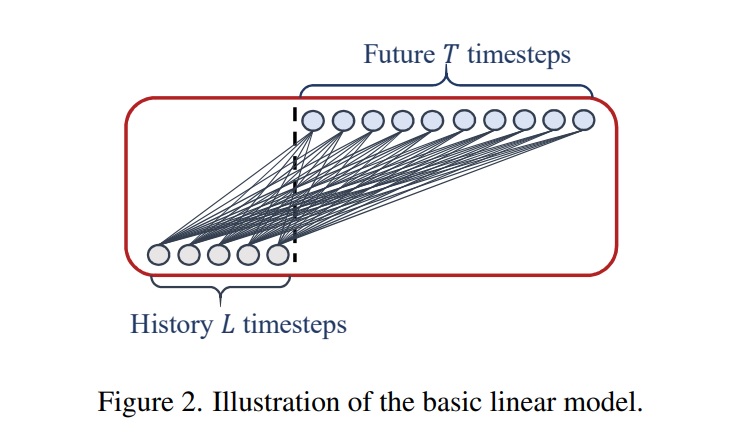
수학적인 표현은 $W\in R^{T\times L}$이 시간 축에서의 linear layer라고 할 떄, $\hat{X_{i}} = WX_{i}$이다.
$\hat{X_{i}}$과 $X_{i}$은 각각 prediction과 i번째 변량의 input이다.
LTSF-Linear은 서로 다른 변량끼리 weight를 공유하고 어떠한 spatial correlation을 모델링하지 않는다
오직 temporal만 모델링한다는 소리
LTSF-Linear은 linear model의 집합이다.
Vanilla Linear은 1층 linear 모델이다. 서로 다른 분야의 time series를 다루기 위해(예를 들어 경제, 교통, 에너지 등) 우리는 2가지 전처리 방법으로 DLinear, NLinear을 소개한다.
구체적으로 DLinear은 Autoformer와 FEDformer에서 사용한 decomposition의 조합을 linear layer에서 사용하는 것이다.
먼저 raw data input을 moving average를 이용하여 trend component로 decompose하고 나머지는 seasonal component로 분해한다.
그때 2개의 1층 linear layer는 각각의 component에 적용되어 2개의 feature를 sum하여 마지막 prediction을 만들어낸다.
명백히 trend를 다룸으로써 DLinear은 data에 trend가 있을 때 vanilla linear의 성능을 높여준다.
한편 LTSF-Linear의 성능을 높이기 위해 데이터셋의 분포이동(distribution shift)이 있을 때, NLinear은 먼저 input에 sequence의 마지막 값(last value)을 빼준다.
그때 input은 linear layer로 들어가고 빼진 부분(subtract part)은 마지막 prediction 전에 다시 더해진다(add back)
(residual connection이랑 좀 비슷한듯)
NLinear에서 subtraction과 addition은 input sequence를 위한 단순한 normalization이다.
6. experiments
6.1 experimental settings
1) dataset
우리는 광범위하게 사용되는 9가지 현실세계 데이터셋, ETT(Electricity Transformer Temperature, ETTh1, ETTh2, ETTm1, ETTm2), Traffic, Electricity, Weather, ILI, Exchange-Rate 등을 사용하여 실험을 수행하였다.
그들은 모두 다변량 시계열 자료이다. 우리는 Appendix에 데이터 설명을 남겨두었다.
2) Evaluation metric
이전 연구들을 따라 우리는 Mean Squared Error(MSE)와 Mean Absolute Error(MAE)를 성능 비교를 위한 핵심 지표로 사용했다.
3) Compared methods
우리는 5개의 현재 transformer 기반의 방법인 FEDformer, Autoformer, Informer, Pyraformer, LogTrans를 포함시켰다.
게다가 우리는 naive DMS 방법으로 Closest Repeat로 window에서 마지막 값을 반복하는 방법인데 또 다른 단순 베이스라인으로 포함시켰다.
FEDformer의 2가지 변형이 있기때문에 우리는 Fourier transform을 사용한 더 나은 성능을 보이는 FEDformer을 가지고 비교를 수행했다.
6.2 comparison with transformer
1) quantitative result

우리는 위 표에서 모든 언급된 transformer들을 이전 연구들의 세팅에 따라 9개의 벤치마크에서 평가를 수행했다.
놀랍게도 LTSF-Linear의 성능이 SOTA인 FEDformer을 대부분의 케이스에서 다변량 예측에서 20%~50% 향상이 있다
LTSF-Linear은 심지어 변량간의 correlation을 모델링하지 않음에도 불구하고 말이다.
다른 time series 벤치마크에서 NLinear, DLinear은 분포이동(distribution shift)과 추세 계절성(trend-seasonality feature)을 다루는데 우수하다는 것을 보여준다.
우리는 또한 ETT 데이터셋의 단일변량 예측을 appendix에 제공하였는데, LTSF-Linear이 여전히 transformer 기반의 LTSF 솔루션보다 큰 격차로 성능을 뛰어넘고 있다.
FEDformer은 ETTh1에서 경쟁력 있는 예측 정확도를 보여주고 있다.
이것은 왜냐하면 FEDformer이 고전적인 time series 분석 기법으로 frequency processing(time series에 inductive bias를 주입)같은 방법을 사용하여 시간 성분을 추출하는데 이점이 있기 때문이다.
요약하자면, 이런 결과들이 복잡한 transformer 기반의 LTSF 솔루션이 현존하는 9개의 벤치마크에서 겉보기에는 효과가 없다는 것이며 반면 LTSF-Linear은 강력한 베이스라인이 될 수 있다는 것이다.
다른 흥미로운 관찰은 naive Repeat방법이 long term seasonal data(예를 들어 electricity, traffic)에서 최악의 결과를 보여준다고 할지라도 놀랍게도 Exchange-Rate(약 45%)에서는 모든 transformer 기반의 방법보다 성능이 좋다는 것을 볼수 있다.
이것은 transformer 기반의 솔루션에서 trend에 대한 잘못된 prediction이 주된 원인이고, training 데이터에서 급격한 변화에 대한 overfitting이 있는 것 같아서 , 상당한 정확도 degradation을 낳기 때문이다.
대신에 Repeat는 bias를 가지고 있지 않다.
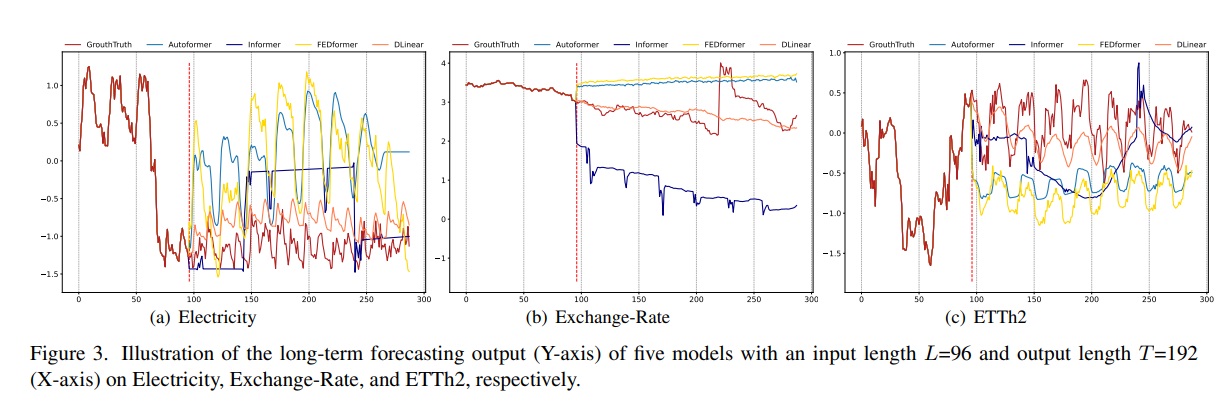
2) qualitative result
위 그림에서 볼 수 있듯이 우리는 3개의 선택된 time series 데이터에 대해 transformer 기반의 솔루션과 LTSF-Linear에 대해 prediction을 그려보았다.
Electricity, Exchange Rate, ETTh2는 각각 서로 다른 temporal pattern을 보인다.
input 길이는 96 step, output은 336 step이고, transformer은 Electricity, ETTh2에서 미래 데이터의 scale, bias를 예측하지 못했다.
게다가 그들은 Exchange Rate같은 비주기적인 데이터에서 적절한 트렌드를 예측하기 어려워한다.
이러한 현상은 LTSF task에서 현존하는 transformer 기반의 솔루션의 부정확성을 보여준다.
6.3 more analyses on LTSF-Transformers
1) can existing LTSF-Transformers extract temporal trelations well from longer input sequence?(LTSF-Transformer들은 긴 input sequence에서 시간적 관계를 잘 추출할 수 있는가?)
###
window는 딥러닝 NLP에서 sliding window할때 그 window를 말하는듯
따로 정리해놔야겠다
###
look back window의 크기가 시계열 데이터에서 얼마나 많이 배울 수 있을지를 결정하기 때문에 예측 정확도에 크게 영향을 미친다.
일반적으로 말하자면, 강력한 TSF model의 강력한 시간 관계 추출 능력은 더욱 큰 look back window size에서 더 나은 결과를 달성할 수 있어야한다.
input의 look back window size의 영향을 연구하기 위해 우리는 T=720인 long term forecasting에서
$L\in \{24,48,72,96,120,144,168,192,336,504,672,720\}$의 window size로부터 실험을 수행했다.
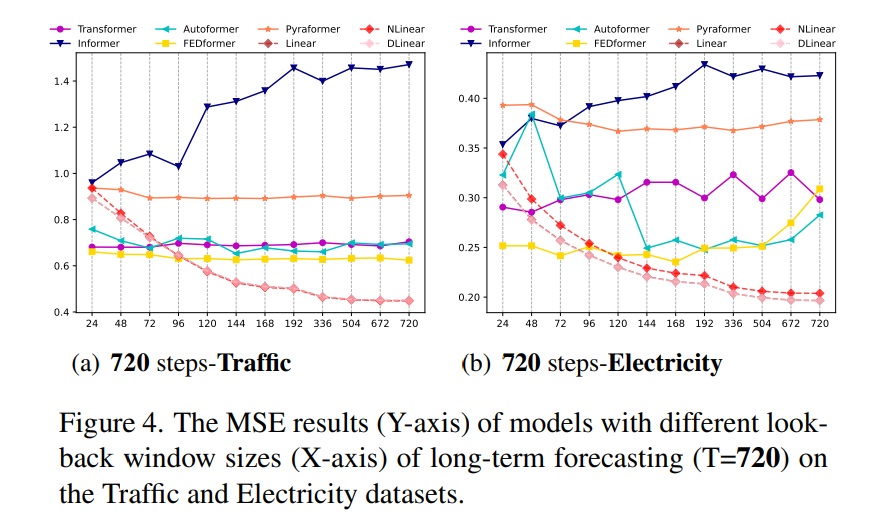
위 그림은 2가지 데이터셋에 대하여 MSE 결과를 보여준다.
이전 연구와 비슷하게 현존하는 Transformer 기반의 모델들의 look back window의 크기가 성능이 악화되거나 안정적이다.
대조적으로 LTSF-Linear의 성능은 look back window의 크기가 커질수록 모두 상당히 증가했다.
그러므로 현존하는 솔루션들은 더욱 긴 sequence가 주어진다면, 시간적 정보를 추출하는 대신에 시간적 noise에 overfitting 되는 경향이 있고 size 96에 대부분의 transformer 모델들이 적합하다.
추가적으로 우리는 Appendix에 더욱 양적인 결과를 제공했고, 거의 모든 케이스에서 우리 결론이 맞다는 것을 보여준다.
2) What can be learned for long-term forcasting?(long term forecasting을 위해 무엇을 배울 수 있는가?)
look back window에서 시간적인 dynamics가 short term series forecasting의 예측 정확도에 상당히 영향을 미치는 반면에 우리는 long term forecasting은 모델이 주기적인 성분을 잘 포착할 수 있는가에 의존한다고 가정했다.
그것은 예측 길이가 길어질수록 look back window 그 자체는 덜 영향을 미친다는 것이다.
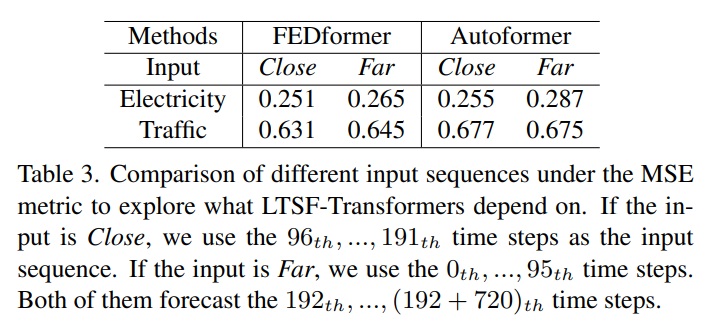
우리 가설을 입증하기 위해 위 표3은 동일한 720 step에서 서로 다른 look back window로 예측 정확도를 비교한 것이다.
Close라고 써진 것은 원래 input L=96 세팅이고 Far이라고 써진 것은 원래 96 time step 이전에 나오는 더 긴 input L=96 세팅이다.
실험 결과 SOTA transformer들의 성능이 약간 떨어졌고 이는 이런 모델들이 인접한 time series에서 비슷한 시간적 정보만을 포착한다는 것을 보여준다.
데이터셋의 고유한 특성을 포착하는 것이 일반적으로 많은 수의 parameter를 요구하지 않기 때문에 다시 말하면 하나의 parameter가 주기성을 표현할 수 있다는 것이다.
너무 많은 parameter가 overfitting을 낳고 이는 부분적으로 왜 LTSF-Linear들이 transformer 기반의 방법보다 더 나은지를 설명한다.
3)Are the self attention scheme effective for LTSF?(self attention들이 long term series forecasting에 효과적인가?)
우리는 현존하는 transformer에 있는 이런 복잡한 디자인이 정말 중요한지 아닌지 입증했다.
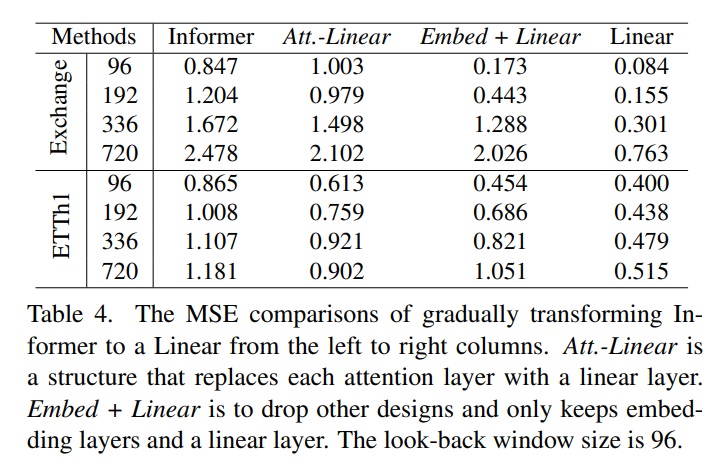
위 표 4는 우리가 점진적으로 Informer에서 Linear로 바꿔가는 과정을 보여준다.
먼저 우리는 각각의 self attention을 linear layer로 대체하였고 이를 att-linear로 썼다. 왜냐하면 weight를 동적으로 바꿔서 self attention layer를 fully connected layer로 간주할 수 있기 때문이다.
게다가 우리는 다른 보조 디자인(예를 들어 FEN)을 Informer에서 버려서 embedding layer와 linear layer를 남겼고 이를 Embed+Linear라고 썼다.
마지막으로 우리는 하나의 linear layer만 남겨 단순화하였다.
놀랍게도 Informer의 성능이 단순해질수록 좋아졌고, 이는 현존하는 LTSF benchmark에서는 적어도 self attention이나 다른 복잡한 모듈은 필요없다는 것을 보여준다.
4) Can existing LTSF-Transformers preserve temporal order well?(현존하는 LTSF-Transformer들이 시간적 순서를 잘 보존하는가?)
self attention은 본질적으로 순열불변(permutation-invariant)이라서, 다시말하면 순서에 무관하다.
그러나 time series forecasting에서는 sequence의 순서가 종종 핵심적인 역할을 한다.
우리는 현존하는 transformer 기반의 방법들이 positional embedding, temporal embedding이 있더라도 여전히 시간적 정보를 잃어버린다고 주장한다.
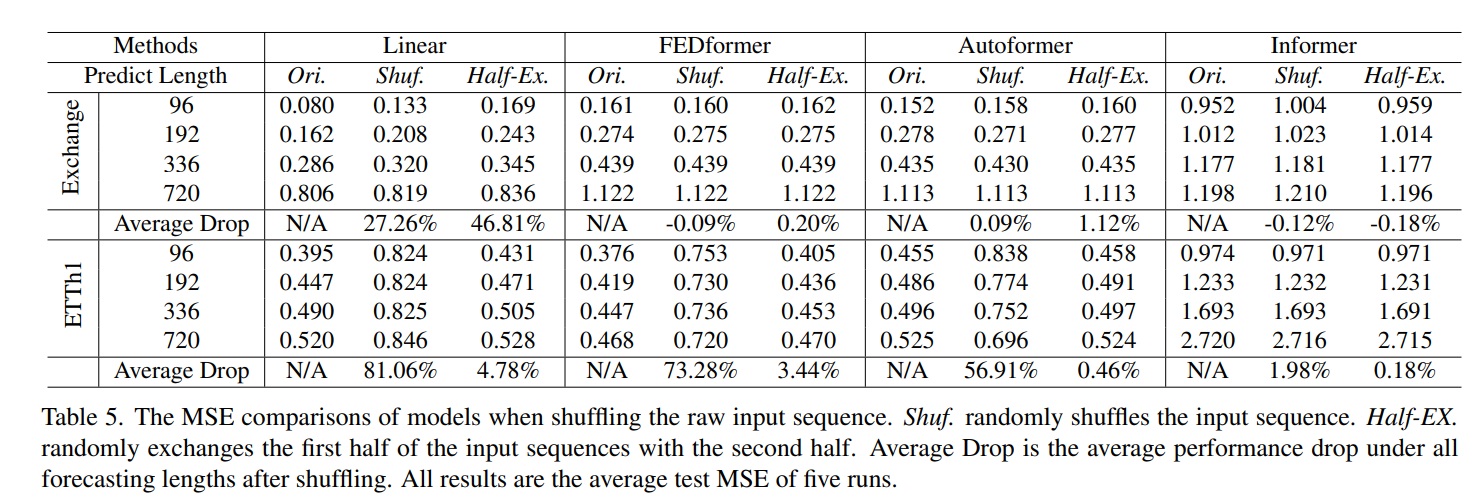
2가지 shuffle 전략이 있는데 Shuf.는 전체 input을 랜덤하게 shuffle한것이고 Half-EX.는 input sequence의 첫 절반을 두번째 절반으로 바꾼 것이다.
흥미롭게도 Exchange Rate에서 원래 세팅과 비교할 때 모든 transformer 기반의 방법의 성능은 input sequence를 랜덤하게 섞더라도 떨어지지 않았다.
대조적으로 LTSF-Linear은 상당히 손실을 입었다.
이것은 서로 다른 positional, temporal embedding을 가지는 LTSF-Transformer들이 제한적인 시간적 관계를 보존하며 noisy financial data에 overfitting되는 경향이 있다는 것을 보여주고
반면 LTSF-Linear은 순서를 자연스럽게 모델링하고 더 적은 parameter로 overftting을 피하고 있음을 보여준다.
순서를 섞었는데도 성능이 그대로라는 것은 순서를 생각하고 있지 않다는 얘기겠지..
ETTh1 데이터셋에서는 FEDformer와 Autoformer가 time series inductive bias를 모델에 도입했고 그들이 Exchange Rate보다 데이터셋이 주기성같은 분명한 시간적 패턴을 가지고 있을 때 특정한 시간적 정보를 잘 추출할 수 있다.
그러므로 2개의 transformer들이 Shuf에서 73.28%, 56.91%의 성능이 떨어졌다는 것을 보여주고 있다. 이는 전체적인 순서 정보를 잃어버렸다는 것을 보여준다.
게다가 Informer은 여전히 Shuf와 Half-Ex에서 덜 떨어지고 있다. 왜냐하면 시간적인 inductive bias를 가지고 있지 않아서 그렇다.
전반적으로 LTSF-Linear의 성능이 평균적으로 모든 경우에 transformer 기반의 방법보다 더 떨어졌으며 이는 현존하는 transformer들이 시간적인 순서를 잘 보존하지 못한다는 것을 보여준다.
5) How effective are different embedding strategies?(서로 다른 embedding 전략이 얼마나 효과적인가?)
우리는 transformer 기반의 방법들에 사용된 position, timestamp embedding들의 이점을 연구했다.
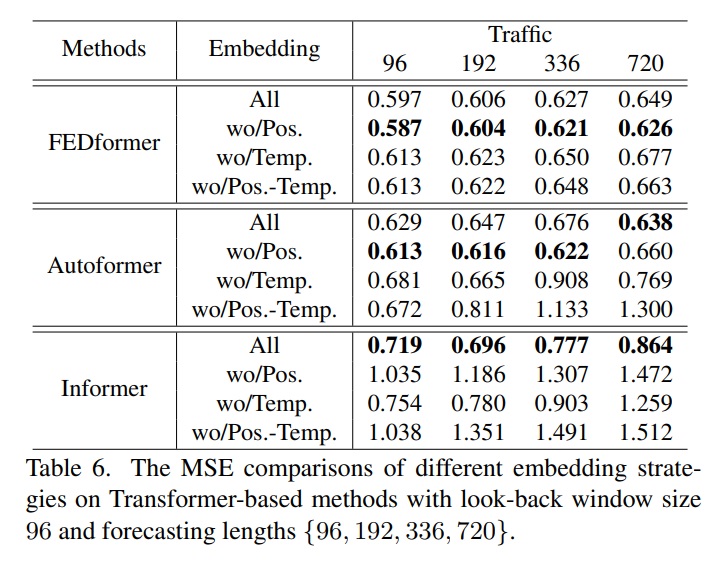
표 6은 Informer의 예측 오차가 positional embedding이 없을 때 상당히 증가했음을 보여준다
timestamp embedding이 없을 때는 예측 길이가 길어질수록 성능에 점진적으로 데미지를 입힌다는 것을 보여준다.
Informer은 각 token마다 single time step을 사용하기 때문에 토큰에 시간적 정보를 도입하는 것이 필수적이다.
반대로 토큰에 single time step을 사용하는 것보다 FEDformer와 Autoformer에서는 timestamp의 input sequence에 시간적 정보를 embedding한다.
그러므로 그들은 fixed positional embedding이 없을 때 더 나은 성능을 보여준다.
그러나 timestamp embedding이 없을 때는 Autoformer은 전체 시간적 정보를 잃어버리기 때문에 급격하게 성능이 떨어진다
대신에 FEDformer에 소개된 frequency-enhanced module덕분에 시간적 inductive bias를 도입하여 position, timestamp embedding을 제거하는 것에서 덜 성능 손해를 입는다.
6) Is training data size a limiting factor for existing LTSF-Transformer?(training data 사이즈가 현존하는 LTSF-Transformer들에 제한요소인가?)
누군가는 transformer 기반의 솔루션의 안좋은 성능들이 벤치마크 데이터셋의 크기가 작기때문이라고 주장한다.
computer vision이나 NLP와는 다르게 TSF는 모아진 time series에서 수행되고 training data size를 증가시키기 어렵다.
사실상 training data size가 실제로 모델 성능에 상당히 영향을 미치는 것은 분명하다.
따라서 우리는 Traffic에서 실험을 수행하여 전체 데이터셋 (17544*0.7시간, Ori)에서 training한 모델의 성능과 더 적은 데이터셋 (8760시간, 즉 1년?, Short)에서 training한 모델의 성능을 비교했다.

위 표 7은 예측 오차를 보여주는데 감소된 training data에서 오히려 대부분 오차가 적다는 것을 알 수 있다.
이것은 아마도 전체 데이터가 불완전한 데이터 크기보다 더 분명한 시간적 정보를 보존하기 때문이다.
우리는 training을 위해 더 적은 데이터를 사용해야 한다는 것에 결론을 내릴 수는 없었지만 이는 training 데이터의 크기가 Autoformer와 FEDformer의 성능을 제한하는 이유가 아니라는 것을 입증한다.
7) Is efficiency really a top-level priority?(효율성이 정말 최우선순위인가?)
현존하는 LTSF-transformer들이 원래 transformer의 $O(L^{2})$복잡도가 LTSF 문제에 감당할 수 없다고 주장한다.
비록 그들이 이론적인 시간,메모리 복잡도를 $O(L^{2})$에서 $O(L)$으로 개선했다고 할지라도
장치에서 실제 시간복잡도와 메모리 복잡도가 개선되었는지
메모리 이슈가 오늘날의 GPU(예를 들어 NVIDIA Titan XP here)에서 받아들일수없고 시급한 문제인지
가 불분명하다.
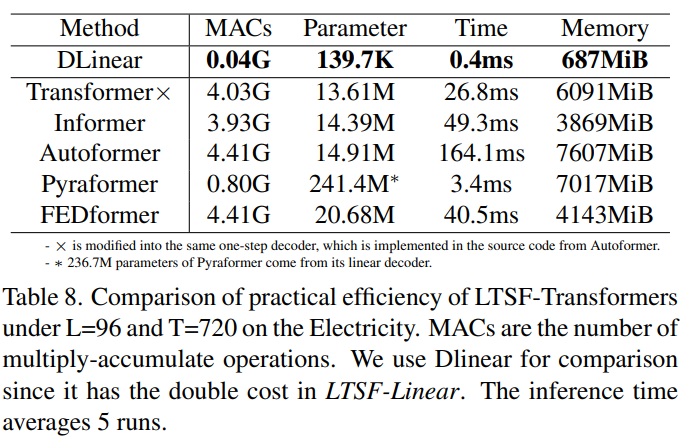
위 표 8은 5번 inference하여 평균적인 효율성을 비교했다.
흥미롭게도 원래 transformer(DMS decoder를 사용)와 비교해서 대부분의 transformer의 변형들이 비슷하거나 더 안좋은 inference time, parameter를 실제로 보여주고 있다.
이것은 실제 추가한 여러 디자인들이 실제 비용을 더 높인다는 것을 보여준다.
게다가 원래 transformer 의 메모리 비용은 output L=720이더라도 실제로 받아들일만하다. 이는 적어도 현존하는 벤치마크에서는 transformer의 메모리효율성의 중요성을 약화시킨다.
7. Conclusion and Future work
1)conclusion
이 논문은 long term time series 예측 문제에서 선호되는 transformer 기반의 솔루션의 효율성에 의문을 제기했다.
우리는 정말 단순한 linear model인 LTSF-Linear을 우리 주장을 입증하기 위해 DMS forecasting의 베이스라인으로 사용했다.
우리의 기여점이 제안한 linear model에 있지 않고 오히려 중요한 의문인 놀라운 비교, 그리고 왜 LTSF-transformer가 이 논문에서 주장한 것처럼 다양한 측면에서 효율적이지 않은지를 주장한 것에 있다.
우리는 정말로 우리의 포괄적인 연구들이 이 분야에서 미래의 연구에 이점을 줄 수 있기를 바란다.
2) Future work
LTSF-Linear은 제한된 모델 능력을 가지고 있고 정말 단순하지만 미래 연구를 위해 강력한 해석가능성을 가지고 있는 경쟁력 있는 베이스라인일 뿐이다.
예를 들어 1층 linear network는 변화하는 점에 의한 temporal dynamics를 포착하기 어렵다.
그 결과로 우리는 새로운 모델 디자인, 데이터 처리, LTSF 문제를 다루는 벤치마크의 등장에 대한 잠재력이 있음을 믿는다.
#############
누구나 의심하지 않을 정도로 훌륭한 transformer에 의문을 품고 놀라운 통찰을 보여준 논문?
오히려 단순하고 기본적인 모델이 더 성능이 좋음을 입증한 논문
https://paperswithcode.com/paper/are-transformers-effective-for-time-series
Papers with Code - Are Transformers Effective for Time Series Forecasting?
🏆 SOTA for Time Series Forecasting on ETTh2 (720) (MAE metric)
paperswithcode.com

