1. GRU(Gated Recurrent Unit)
LSTM의 경량화, 적은 메모리와 빠른 계산시간
LSTM의 cell state와 hidden state를 하나의 hidden state로 일원화
하나의 input gate만 활용함

이전 hidden vector $h_{t-1}$과 input gate에서 계산한 $\tilde{h_{t}}$의 가중평균 형태로 새로운 hidden vector $h_{t}$가 업데이트되어 나감
하나는 다음 step의 hidden vector $h_{t}$로 나가고 예측이 필요하다면 똑같은 hidden vector $h_{t}$가 output layer로 들어가 예측을 수행
흐름과 식을 잘 봐야함
이전 hidden vector $h_{t-1}$가 input gate로 그대로 들어가서 input x와 적절하게 섞이면서 $z_{t}$, $r_{t}$를 내놓는다
LSTM과 GRU는 성능이 비슷비슷하다. 상황에 맞게 적절하게 사용
2. backpropagation in LSTM,GRU
LSTM의 backpropagation은 cell state로 gradient가 흘러들어간다.
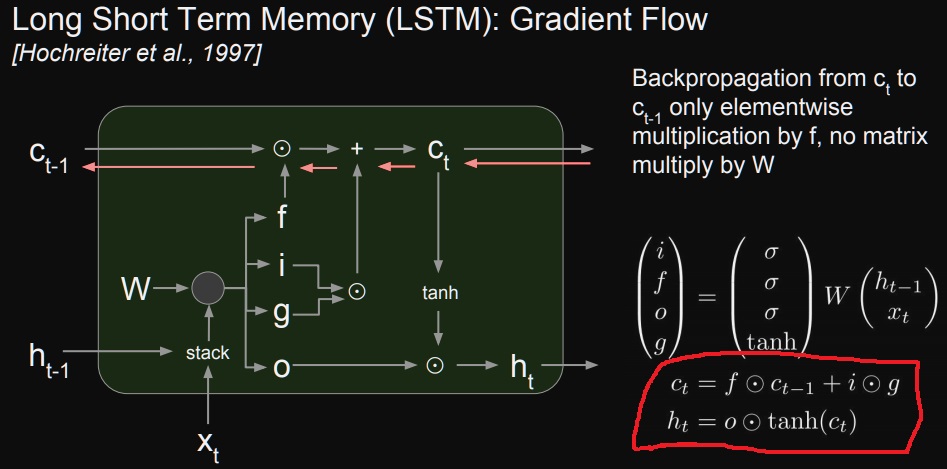
LSTM의 식을 보면 loss를 가중치로 미분하는데 hidden vector $h_{t}$를 이용해서 prediction을 하므로 hidden vector $h_{t}$를 미분하면 된다.
그러면 이제 cell state의 미분을 수행해야하는데 식을 다시 써보면

Vanilla RNN에서 동일한 가중치 행렬 $W_{hh}$가 계속 곱해지는 형태가 나오는 반면에 cell state는 forget gate의 값이 계속 곱해진다.
forget gate의 값은 시점마다 달라지는 값이다.
동일한 값의 합성곱이 아니라서 gradient vanishing/gradient exploding 현상이 상대적으로 덜 일어난다.

수식으로부터 알 수 있는 점은 cell state로 gradient가 계속 흐르게 된다는 것
수식으로도 알 수 있지만 gradient vanishing이나 exploding이 vanilla RNN에 비해 안 일어날 가능성이 높은거지 일어날수도 있다는게 중요하다
그리고 위에서 주어진 cell state를 이전 cell state에 대해 미분하면 forget gate값의 곱으로 나타난다.
forget gate값은 sigmoid로 인해 (0,1)의 값이므로 계속 곱해지면 gradient vanishing이 언젠가는 일어날것이긴 함.
그러나 이 값이 1에 가깝다는 것은 그만큼 정보를 오래도록 전달한다는 의미다
(왜 인지 모르겠다면 forget gate가 무엇을 구하는지 의미를 다시한번 봐보아라)
>> cell state의 1-f만큼 버리고 f만큼 가져가거든
오래도록 전달할수록(f가 1에 가까울수록) gradient(f의 곱)도 오래도록 소멸하지 않는다는 점에서 모형의 이름이 LSTM(Long Short Term Memory)으로 되게 잘 붙었다

'딥러닝 > NLP' 카테고리의 다른 글
| seq2seq model이란? (0) | 2022.04.05 |
|---|---|
| RNN을 이용한 글자 수준의 언어 모델(Character-level language model) (0) | 2022.04.01 |
| RNN을 개선한 LSTM과 GRU 구조 알아보기 (0) | 2022.03.16 |
| Word2Vec의 sliding window 완벽하게 이해하기 (0) | 2022.02.28 |
| RNN의 기본 구조 이해하기 (0) | 2022.02.19 |

