RNN의 기울기 소실(gradient vanishing) 문제

1. RNN의 역전파(Backpropagation through time)

 

빨간색은 그래디언트가 흘러들어가는 방향이다.

 

그림으로 직관적으로 나타낸 RNN의 역전파과정

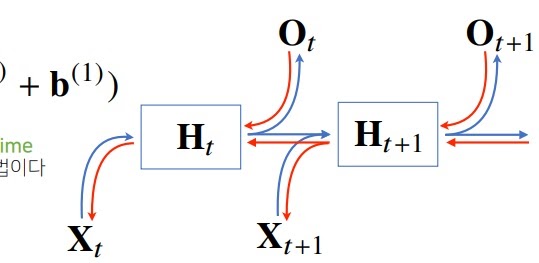
Hidden layer에 대한 그래디언트 하나를 직접 계산해보면

 

 

빨간색 부분에 주목해보자.

 

f의 미분값이 1보다 크면 곱해지면서 점점 커질 것이고 gradient exploding 현상이 일어난다.

 

즉 그래디언트가 매우 커져서 학습이 전혀 안된다는 것.

 

반대로 f의 미분값이 1보다 작으면 곱하면서 점점 작아질 것이고 gradient vanishing 현상이 일어난다.

 

gradient가 0이 되어버리니 학습이 안된다는 소리임.

 

수식으로 더 써보면 그림과 같다.

 

 

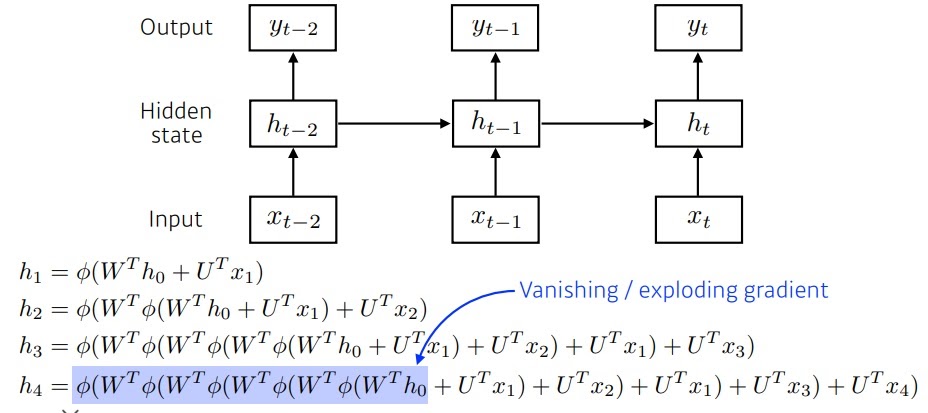
잠재변수가 가중치행렬과 활성화함수의 반복적인 곱으로 이루어진다.

 

직관적으로 활성화함수가 시그모이드라면 정보를 압축하는 역할을 하는데(0과 1 사이)

 

계속 곱하면서 너무 압축해버리면 정보가 없어지잖아.

 

만약 활성화함수가 ReLU라면 가중치행렬 WT이 양수인 경우 그대로 뱉어나오니까 이게 계속 곱해지면서

 

너무 커지니까 gradient exploding현상이 일어남 학습이 안돼 

 

 

2. RNN의 기울기 소실 문제

 

기울기가 소실되면 특히 시퀀스가 긴 데이터의 경우 정보 업데이트가 안되니까 문제가 심각하다.

 

기울기 소실 문제의 해결책으로 일부 길이를 적절하게 끊어서 계산하는 truncated BPTT가 고안되었다

 

truncated BPTT를 직관적으로 나타낸 그림

 

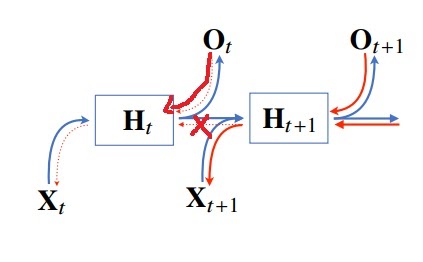
그러나 이것도 완전한 해결책은 아니다. 이것을 극복하기 위해 LSTM, GRU 등이 고안되었다.