1. 순열 사이클
1부터 n까지 정수 n개로 이루어진 배열을 순열이라고 부른다.
예를 들어 [3,2,4,5,1]은 길이가 5인 순열이다.
배열의 인덱스를 '현재 위치', 배열의 값을 '다음에 갈 곳'으로 생각하고 인덱스 > 값으로 향하는 방향 그래프를 만들 수 있다.
즉, [3,2,4,5,1]은 1 > 3, 2 > 2, 3 > 4, 4 > 5, 5 > 1로 간선을 이으면 다음과 같이 방향 그래프를 만들 수 있다.

위 그래프는 2개의 사이클 1 > 3 > 4 > 5, 2 > 2가 있다.
이 사이클들을 순열 사이클이라고 부른다.
전체 순열을 여러개의 독립적인 순열 사이클로 분할하는 것을 '순열 사이클 분할'이라고 부른다.
길이 n인 순열에는 반드시 사이클이 생긴다.
왜냐하면 먼저 1부터 n까지 1개씩만 존재하기 때문이다.
각 노드는 오직 하나의 다른 곳만 가리키며, 어떤 곳에서 시작해서 n+1번 이동하면 비둘기집 원리에 의하여
적어도 한번은 반드시 이미 방문했던 곳을 또 방문하게 된다.
그리고 반드시 출발점으로 돌아오게 되어있다.
왜냐하면 순열이기 때문에 각 노드는 반드시 하나의 노드만을 가리키기 때문이다.
다음과 같이 A > B > C > D > B로 돌아오는게 가능할까?
이 경우는 B에 들어오는 간선이 2개인데 이것은 불가능하다.
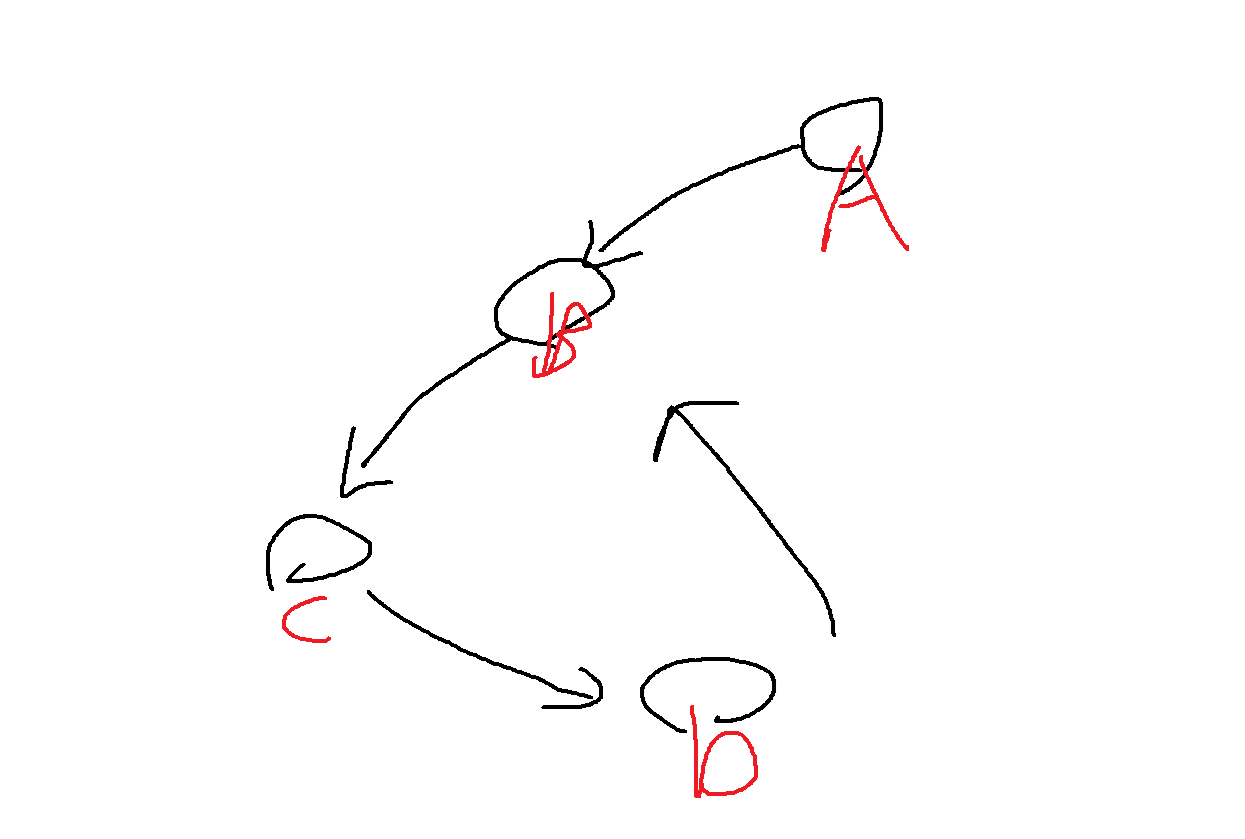
A,B,C,D가 각각 1,2,3,4 인덱스라고 한다면,
위 그림은 1 > 2, 2 > 3, 3 > 4, 4 > 2이므로 [2, 3, 4, 2]로 순열이 아니다.
즉 각 노드 번호는 인덱스이며, 인덱스 > 배열의 값으로 만드는 순열의 그래프인데...
순열의 원소들은 모두 중복되지 않고 1,2,3,..,N 각각 1개씩이므로, 각 값이 2개의 들어오는 간선이 존재하면 모순이다.
따라서 순열에서 인덱스 > 값 그래프를 만들면 반드시 사이클이 생긴다.
------------------------------------------------------------------------------------------------------------------------------------------------
2. 순열 사이클 분할
순열 사이클 분할은 O(N)에 가능하다.
https://www.acmicpc.net/problem/10451
순열에서 인덱스 > 값 그래프를 만들때 순열 사이클의 개수를 구하는 문제
visited 배열을 만들고, 1번부터 n번까지 순회하면서, 아직 방문하지 않으면,
현재 번호 curr = i로 두고, visited[curr] = 1이 될때까지 visited를 체크함
다음 번호는 curr = A[curr]
이 과정이 끝나면 한 사이클을 돈 것이므로 사이클 개수를 +1
from sys import stdin
t = int(stdin.readline())
for _ in range(t):
n = int(stdin.readline())
A = [0] + list(map(int,stdin.readline().split()))
visited = [0]*(n+1)
count = 0
for i in range(1,n+1):
if visited[i] == 0:
curr = i
while visited[curr] == 0:
visited[curr] = 1
curr = A[curr]
count += 1
print(count)
3. 기본 연습문제
https://www.acmicpc.net/problem/8636
1번부터 n번까지 각 사람이 왼쪽에 앉은 사람의 번호를 지적할때, 테이블이 몇개인지 구하는 문제
각 사람을 인덱스, 왼쪽에 앉은 사람의 번호를 배열의 값으로 해서 순열 그래프를 만들고,
이 순열 그래프의 사이클 개수를 구하면 된다.
https://www.acmicpc.net/problem/22144
순열 P와 특수한 순열 Z = [2,1,3,4,...,N]이 주어진다.
각 순열은 i는 P[i]로 옮기거나, Z[i]로 옮길 수 있다는 뜻
P와 Z를 무한히 원하는 순서대로 적용했을때 A위치를 B 위치로 옮길 수 있는지 체크하는 문제
조금? 생각을 해야하는데
P를 순열 사이클 분할하여 각 사이클을 하나의 그룹으로 만들면 각 사이클 내의 원소들은 서로 이동할 수 있다는 뜻
그런데 순열 Z는?
그냥 1번과 2번만 바뀐 순열이다. Z를 어느 순간에 적용한다는 것은 결국 1번과 2번은 서로 왔다갔다 할 수 있다는 뜻
따라서 P의 순열 사이클들을 모두 구하고, 1번이 포함된 사이클과 2번이 포함된 사이클을 합치면 된다.
from sys import stdin
n,m = map(int,stdin.readline().split())
P = [0] + list(map(int,stdin.readline().split()))
#P의 순열 사이클 분할
visited = [0]*(n+1)
g = 1
for i in range(1,n+1):
curr = i
while visited[curr] == 0:
visited[curr] = g
curr = P[curr]
g += 1
#1번이 포함된 사이클과 2번이 포함된 사이클을 합치기
g1 = visited[1]
g2 = visited[2]
for i in range(1,n+1):
if visited[i] == g2:
visited[i] = g1
#A,B의 사이클 번호가 서로 같으면 서로 이동 가능하다는 뜻
for _ in range(m):
a,b = map(int,stdin.readline().split())
if visited[a] == visited[b]:
print('Yes')
else:
print('No')

