1. prime number theorem(소수 정리)
양의 실수 x 이하에 존재하는 소수의 개수를 $\pi(x)$라고 한다면 다음이 성립한다.
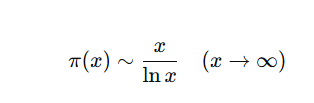
양수 x이하의 소수의 개수는 근사적으로 x/logx개라는 소리다.
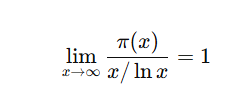
로그 적분 함수 li(x)는 다음과 같이 정의한다.
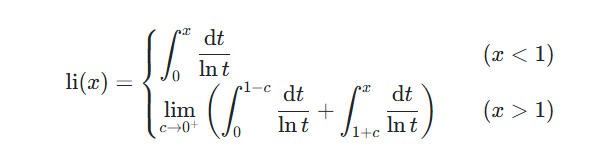
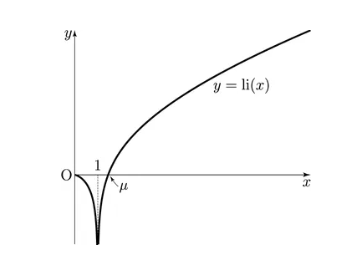
그래프가 다음과 같다.
구간 [0,x]가 아닌 [2,x]에서 로그 적분 함수를 Li(x)로 나타내기도 한다
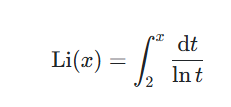
이를 이용해서 다음과 같이 나타내기도 한다.
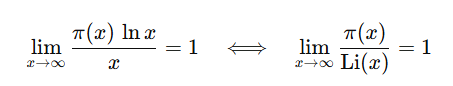
즉, $\pi(x)$는 Li(x)에 근사할 수 있고, 현대에는 이게 더 정확하다고 알려져있다.
2. 소수의 밀도
직관적으로 큰 숫자에서 소수 사이 간격이 점점 커진다는 것을 알 수 있다.
에라토스테네스의 체로 구해보면 알수 있다
그렇게 차이나지는 않네 흠..

양수 x에 대하여 x 근방에서 소수가 나타날 확률은
$\pi(x+1) - \pi(x) \approx \frac{1}{logx}$이므로, x가 커질수록 logx도 커져서, 점점 소수가 등장할 가능성이 희미해진다.
3. n번째 소수
소수 정리로부터 n번째 소수는 nlogn에 근사한다는 것을 알 수 있다.
prime counting function $\pi(x)$는 x 이하의 소수의 개수이므로, n번째 소수를 $p_{n}$이라고 한다면,
$\pi(p_{n}) = n$
$\pi(x) \approx \frac{x}{logx}$에 $x = p_{n}$을 대입하면, $\pi(p_{n}) = n \approx \frac{p_{n}}{logp_{n}}$이다.
따라서, $p_{n} \approx nlogp_{n} \approx nlogn$
664579번째 소수는 9999991인데

그렇게 비슷하진 않네..
조금 더 정확한 근사가 n(logn + log(logn))-1)이라고 함..
4. 특정 구간 내의 소수의 개수
segmented sieve는 특정 구간 내의 소수를 찾는 알고리즘인데
에라토스테네스의 체 변형 segmented sieve 배우기
에라토스테네스의 체 변형 segmented sieve 배우기
https://deepdata.tistory.com/393 소수를 빠르게 구하는 에라토스테네스의 체 알고리즘1. 소수를 구하는 방법 컴퓨터가 주어진 수 n이 소수인지 판단할려면 어떻게 해야할까? 1부터 n까지 n에 나눠보면서
deepdata.tistory.com
그러면 특정 구간내의 소수는 대략적으로 몇개나 있을까?
알고리즘 문제에 등장할 수 있는 [L,R]에 대하여, R-L이 $10^{7}$정도라면 몇개나 있을까?
소수 밀도는 x가 작을 수록 소수가 더 많이 등장한다는 것을 알려주므로, R에 대하여 소수가 가장 많이 포함될 수 있는 구간은...
[2,R]이다.
$R = 10^{7}$정도라면... 664579개 있으니까 많아야 $10^{5}$개에서 $10^{6}$개 정도?
$R = 10^{6}$정도면 78498개 이 구간 길이면 70000개 정도 있다는거네
5. 연습 문제
[L,U] 구간 내의 소수들에 대하여, 인접한 소수끼리 거리가 가장 가까운 두 소수, 가장 먼 두 소수를 찾는 문제
L,U는 최대 2147483647까지인데, 구간의 길이 U-L이 $10^{6}$
-----------------------------------------------------------------------------------------------------------------------------------
segment sieve의 아이디어를 이용하자.
2147483647의 제곱근은 약 46341정도이며 46341 이하의 소수들을 먼저 찾는다.
그리고 이 소수들을 이용해서 [L,U] 구간 내에 이 소수들의 배수를 모두 지우고 남은 수들이 [L,U]구간 내의 소수가 된다.
구간 길이가 $10^{6}$인 구간 내의 소수는 70000개 정도 있다는 것을 알고 있다.
그래서 이 구간을 전부 순회해서 인접한 소수간 거리를 모두 찾아봐도 시간은 충분하다
max_v = 2147483647
n = int(max_v**(1/2))
result = [1]*(n+1)
result[0] = 0
result[1] = 0
for i in range(2,int(n**(1/2))+1):
if result[i] == 1:
for j in range(i*i,n+1,i):
result[j] = 0
prime = [i for i in range(2,n+1) if result[i] == 1]
def segment_sieve(l,u):
segment = [1]*(u-l+1)
result = []
for p in prime:
if l % p == 0:
i = l//p
else:
i = l//p+1
i = i * p
if i == p:
i += p
for j in range(i,u+1,p):
segment[j-l] = 0
if l == 1:
segment[0] = 0
for j in range(u-l+1):
if segment[j] == 1:
result.append(j+l)
return result
while 1:
try:
l,u = map(int,input().split())
segment = segment_sieve(l,u)
min_d = 10**18
c1,c2 = -1,-1
max_d = 0
d1,d2 = -1,-1
for i in range(len(segment)-1):
p1,p2 = segment[i],segment[i+1]
if p2-p1 > max_d:
max_d = p2-p1
d1,d2 = p1,p2
if p2-p1 < min_d:
min_d = p2-p1
c1,c2 = p1,p2
if c1 == -1 and c2 == -1 and d1 == -1 and d2 == -1:
print('There are no adjacent primes.')
else:
print(f'{c1},{c2} are closest, {d1},{d2} are most distant.')
except:
break
'정수론' 카테고리의 다른 글
| 에라토스테네스의 체 변형 segmented sieve 배우기 (0) | 2025.06.30 |
|---|---|
| 의외로 모르는 어떤 분수가 유한소수가 될 수 있는 조건 (0) | 2025.04.29 |
| 모든 양의 유리수는 단위분수의 합으로 나타낼 수 있다 (0) | 2025.04.28 |
| 정수의 임의의 거듭제곱들의 합을 바라보는 놀라운 방법 (0) | 2025.02.11 |
| 나눗셈 실수오차가 생긴다면 직접 나눗셈을 구현하기 (0) | 2024.09.26 |

