i번째 놀이기구 이용권의 횟수가 A[i]로 주어진다
모든 놀이기구를 이용하고 싶은데 연속으로 같은 놀이기구를 사용하지 않는다
최대 몇번 사용가능한가?
A = [1,1,3]이면 3번, 2번, 3번, 1번, 3번으로 5번 가능하다
처음에 생각하기에는 무조건 큰 값끼리 모아서 쌍으로 이용하면 된다고 생각을 했는데
A = [1,2,3,4,5]라고 한다면
5번 이용가능한거랑 4번 이용가능한거 모아서
5 4 5 4 5 4 5 4 이렇게 하면 8번 쓰는거고 5가 1번 남고
[1,2,3,0,1]에서
3,5 해서 3번이 2번 남고
[1,2,2,0,0]에서 3번 2번 가져와서 3,2,3,2 해서 [1,0,0,0,0] 해서 1번을 쓰면 된다는 식으로
n = int(input())
A = list(map(int,input().split()))
A.sort()
count = 0
a = A.pop()
while A:
b = A.pop()
if a < b:
a,b = b,a
count += 2*b
a -= b
if a == 0:
if len(A) > 0:
a = A.pop()
if a > 0:
count += 1
print(count)
근데 틀렸더라 반례가 있나
그래서 우선순위 큐로 매번 두 수를 비교할때 최댓값끼리만 가져오도록
A = [1,2,3,4,5]에서 4번과 5번을 비교해서 [1,2,3,0,1]로 만들고
다음번에는 2번과 3번을 비교해서 [1,0,1,0,1]로 만들어서
다음에는 1번 3번 가져와서 [0,0,0,0,1]로 만들고
마지막 5번 쓰면 끝
import heapq
n = int(input())
A = list(map(int,input().split()))
queue = []
for i in range(n):
heapq.heappush(queue,-A[i])
count = 0
while queue:
a = heapq.heappop(queue)
a = -a
if len(queue) > 0:
b = heapq.heappop(queue)
b = -b
count += 2*b
a -= b
heapq.heappush(queue,-a)
else:
count += 1
break
print(count)
근데 얘도 안되더라 무슨 반례가 있는지는 모르겠지만
이거 해법은 문제를 다르게 생각해서 인덱스를 나열하는거로 생각하는거
A = [1,1,3]이라면
인덱스 기준으로 3,2,3,1,3번 순서대로 사용하면 되니까
이 문제는 인덱스를 서로 연속되지 않게 일렬로 나열할때 얼마나 길게 나열 가능한가?와 같다
그러면 A의 원소중 최댓값 A[m] = max_A을 기준으로 먼저 나열하고 다음에는 다른 원소 A[n1], A[n2], ...를 나열
m, n1, m, n1, m, n1, ....
이렇게 나열하다가 최댓값을 다 썼는데 다른 원소들이 남았다면?
m, n1, m, n1, m, n1, ...., n1, m
만약에 m이 k개 있다면 m과 m 사이의 공간은 k-1개
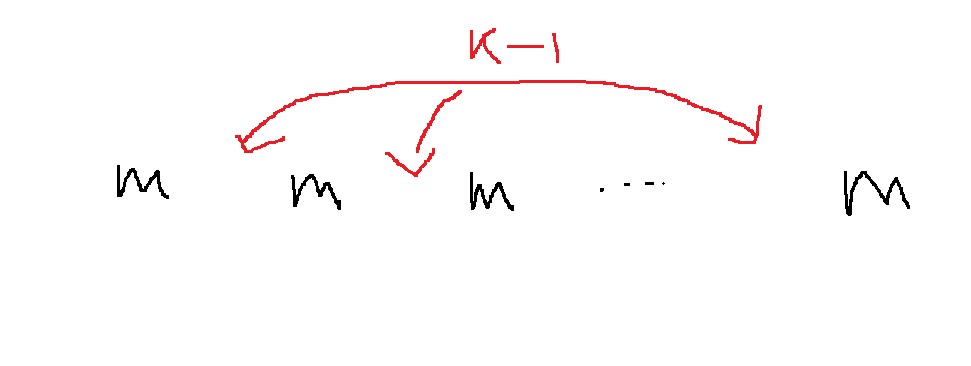
m번이 k개니까 그 사이에 A[m]보다 더 작거나 같은 개수의 n1은 최대 k개 나열할 수 있는데
m,n1,m,n1,....,n1,m에서 만약에 n1이 k개 있다면
m,n1,m,n1,...,n1,m,n1까지 나열할 수 있고 다음에 쓸 수 있는건 n2,n3,...
사실상 m,n1,m,n1,...,n1,m,n1는 초기화나 마찬가지니까 n2부터 차례대로 다시 나열하면 될것
n2,n3,n2,n3,...,n2
마찬가지로 n2가 k개 있다면 n3은 최대 k개 있으므로 k-1개 있다면 n2 사이에 집어넣어서 n2,n3,...,n3,n2
k개 있다면 n2,n3,....,n3,n2,n3으로 하면 끝
또 나머지 n4,n5,... 이렇게도 똑같이 가능
최댓값인 원소의 개수가 x개 있고 나머지 원소의 개수는 r = sum(A) - x
최댓값인 원소의 개수보다 나머지 원소들의 개수가 더 많으면 전부다 일렬로 나열할 수 있다는 관찰을 얻었는데
1) r = x이 정확히 같다면
m,n1,m,n1,...,m으로 최댓값 원소를 다 쓰면 최댓값 사이는 x-1개인데 여기에 나머지 원소들 x-1개를 썼고
나머지 원소 하나 n1을 m 다음에 배치하면 전부 다 쓸 수 있다
r = x+1로 최댓값 원소의 개수보다 1개 더 많다면
m,n1,m,n1,...,m까지 최댓값 원소를 다 쓰고 최댓값 원소 사이는 x-1개인데
나머지 원소는 2개 남았다는거임
그 사이에 들어가는 n1은 최대 x개 있을 수 있으므로 x-1개를 m 사이에 전부 배치하면 1개 남는데
m,n1,m,n1,...,n1,m다음에 n1을 배치하고 그 다음 원소 n2를 n1 다음에 배치해서
m,n1,m,n1,...,n1,m,n1,n2하면 끝
당연하지만 n1이 x개가 아니고 더 적다고 하더라도 m 사이에는 m이 아닌 아무거나 x-1개를 배치하고
나머지 2개는 서로 같든 다르든 상관이 없다
m,n1,....,nk,m에서 나머지 2개가 nx로 같다고 하더라도 m,n1 사이에 넣어도 되고... 적당히 공간을 찾아서 넣을 수 있다는거임
즉 r = x,x+1,x+2,... 면 무조건 일렬로 전부 배치할 수 있다
2) r = x-1은 어떨까
최댓값인 원소의 개수 x개보다 나머지 원소들의 개수 r개가 더 적은 경우
m,n1,m,n1,... 나열하다가 m을 다 쓰기도 전에 n1을 다 써버리는
그래도 m이 x개 있다면 m 사이 공간에는 x-1개 있으므로 r = x-1까지는 다행히 전부 배치할 수 있다
m 사이 공간에 r = x-1개의 나머지 원소들을 배치하면 전부 일렬로 배치할 수 있으니까
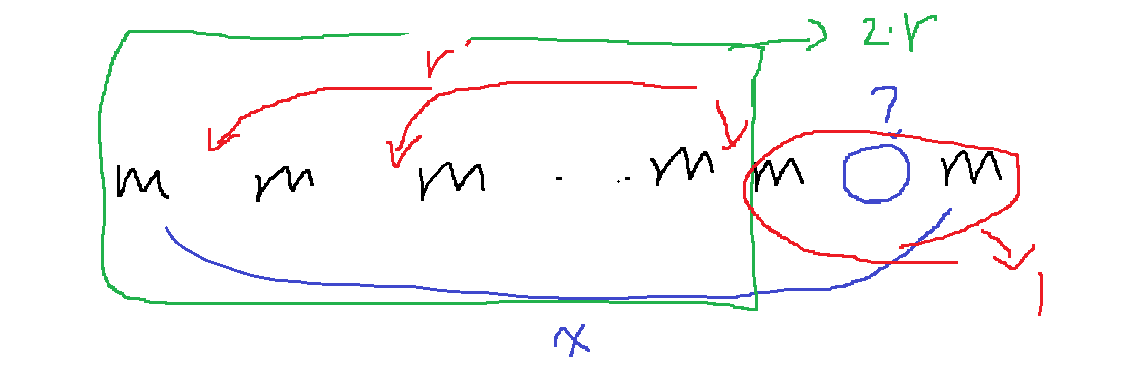
3) 근데 문제는 r = x-2,x-3,...으로 더 적어진다면?
m 사이 공간은 x-1개의 공간이 있는데 r = x-2개이면 x-2개는 채울 수 있는데.. 결국 m 2개가 서로 붙어버리게 된다

따라서 최댓값인 원소 m의 개수 <= 나머지 원소의 개수 r + 1이면 전부 일렬로 배치 가능하므로
전체 원소의 개수만큼 사용 가능
반대로 최댓값인 원소 m의 개수 > 나머지 원소의 개수 r+1이면 최댓값인 원소 m이 결국 붙어버리게 되므로
최댓값이 아닌 나머지 원소 r개의 2배만큼 일렬로 배열할 수 있고
나머지 최댓값인 원소는 1개만 사용가능하게 되므로... 2r+1번 사용 가능
n = int(input())
A = list(map(int,input().split()))
m = max(A)
s = sum(A)
r = s - m
if m <= r+1:
print(s)
else:
print(2*r+1)
'알고리즘 > 그리디 알고리즘' 카테고리의 다른 글
| 올바른 괄호 문자열을 만드는 알고리즘 (0) | 2025.05.26 |
|---|---|
| 인접한 원소의 곱의 합이 최대가 되도록 수열을 만드는 방법 (0) | 2025.02.20 |
| 재배열 부등식(rearrangement inequality)을 이용한 내적의 최대 최소 (0) | 2024.11.22 |
| 기간 제한이 있는 과제들에서 최대 가치를 얻는 그리디 알고리즘 (0) | 2024.06.04 |
| 1부터 n까지 각각 1번씩 정확히 k개의 정수만 사용해서 합을 s로 만드는 그리디 알고리즘 (0) | 2024.05.29 |

