1. overview
matrix가 2차원에서 데이터를 모델링했으면 tensor는 3차원 이상에서 주어진 데이터를 모델링하고자함
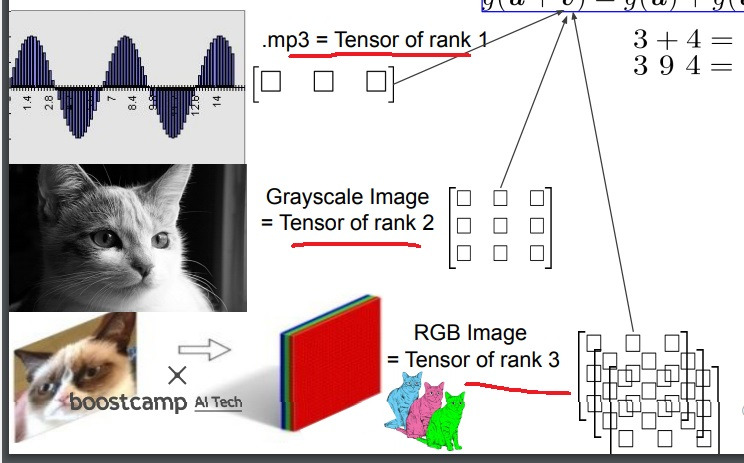
mp3 음성 데이터는 rank1 tensor로 모델링할 수 있고 grey image는 rank2 tensor로 모델링할 수 있고
RGB 이미지는 rank3 tensor로 모델링할 수 있음
2. spectral decomposition
두 벡터 a ∈ $R^{m}$ , b ∈ $R^{n}$에 대하여 a와 b의 outer product는 하나의 m*n행렬 X = a ⊙ b를 나타낸다.
바꿔말해서 하나의 m*n행렬이 두개의 0이 아닌 벡터의 outer product X = a ⊙ b 로 나타낼 수 있으면
행렬 X를 rank one matrix라고 부른다.

비슷하게 3개의 벡터 a ∈ $R^{m}$ , b ∈ $R^{n}$, c ∈ $R^{p}$를 이용하여 outer product를 하면 3차원 tensor x = a ⊙ b ⊙ c를 얻는다.
바꿔말해 3차원 tensor를 0이 아닌 세개의 벡터의 outer product x = a ⊙ b ⊙ c 로 나타낼 수 있으면 x를 rank one tensor라고 부른다

더욱 일반적으로 d개의 벡터 $a_{k} ∈ R^{n_{k}}$ ,k=1,2,...,d를 이용해 outer product를 하면 d차원 tensor x = a1 ⊙ a2 ⊙ a3 ⊙ ... ⊙ ad를 얻는다
반대로 d차원 tensor를 0이 아닌 d개의 벡터의 outer product x = a1 ⊙ a2 ⊙ a3 ⊙ ... ⊙ ad 로 나타낼 수 있으면 rank one tensor라고 부른다.

3. neural network로의 응용
low rank decomposition은 CNN layer에서 low-rank 성질을 가지고 가자는 것으로
fully connected layer를 효율적으로 compressed할 수 있고 low-rank decomposition으로 발전되었지만
convolutional layer에서는 할 수 없었다.?????
CNN에서 fully connected layer부분만 압축하는데 쓸 수 있었다는 이야기인가
spatial decomposition은 h*w filter를 1*w와 h*1 filter로 decomposition하는 방법
channel decomposition은 하나의 convolutional layer를 2개의 convolutional layer로 분해하는데
첫번째는 동일한 filter size를 갖지만 적은 channel을 가지고 두번째는 1*1 convolution을 한다???
depthwise separable convolution은 depthwise convolution을 하고 pointwise convolution을 하는 것이다.
depthwise convolution은 2d channel-wise convolution으로 spatial relationship에 집중하고
pointwise convolution은 1*1 convolution across channel을 통해 cross channel relationship에 주목한다.
channel pruning이란 structured pruning의 일종으로 pruning단위를 channel단위로 하는 방법
필요없는 filter channel을 prune하는 training-free method
network decoupling이란 pretrained CNN을 mobilenet같은 depthwise separable convolution architecture로 transfer하여 CNN을 가속화시키는 training free 방법이다.
accuracy를 손해볼것을 어느정도 감수하고 속도를 높이는데 중점을 둔다
regular convolution을 depthwise separable convolution으로 분리하는 tensor decomposition을 통해 이루어진다.
4. CP decomposition
Canonical Polyadic decomposition
singular value decomposition의 tensor version이 CP decomposition
rank one tensor의 합에 의해 하나의 tensor를 근사시키는 방법
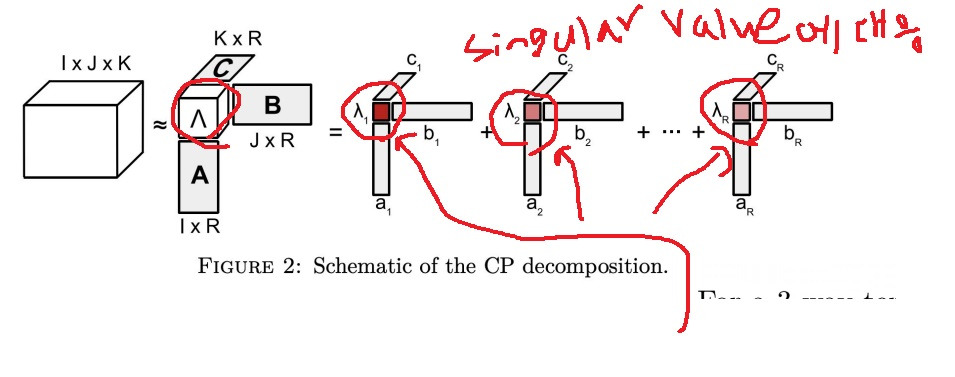
수학적으로 $x \approx \sum_{r = 1}^{R} \lambda a_{r} \circ b_{r} \circ c_{r}...$
5. Tucker decomposition
CP decomposition의 일반화된 version
주어진 tensor의 작은 core tensor와 원래 tensor보다 low-rank인 sub-tensor로 decomposition하는 방법

6. 어떻게 decomposition할 수 있나
matrix decomposition의 경우 characteristic equation을 풀어서 eigenvalue와 eigenvector를 구하는 closed form이 존재해서 대각화를 하면 쉬운데
tensor decomposition은 optimization을 통한 iterative search를 한다
3차원 tensor의 경우 다음과 같은 optimization 문제를 푸는 것과 같다

frobenius norm은 euclidean norm을 tensor에서 구한거
근데 closed form이 없어서 iterative하게 찾는다는 것인데 a,b,c에 initial value를 각각 주고
$|X - \hat{X}|$을 통한 loss를 계산해서 gradient descent 방식으로 근사적으로 찾는거
더욱 근사시키기 위해서 principal한 singular value부분만 남기고 나머지는 모두 버리기도 함

예를 들어 분할된 tensor중에 나머지는 버리고 앞에 singular value가 큰 2개만 사용해서 approximation을 한다
7. CP decomposition과 Tucker decomposition 비교
CP decomposition은 주어진 tensor를 vector들의 outer product인 rank one tensor의 linear combination으로 나타내는것
CP decomposition은 해석에 있어서 유용하다
그런데 rank one tensor들의 일부분만 사용하는 principal component analysis방법을 사용하여
원래 tensor에 approximation한다면 compression에서도 유용할 수 있다

CP decomposition은 해석에 유용하지만 truncation을 하여 일부 rank one tensor의 합으로 근사시킬때 compression에 유용할 수 있다
Tucker decomposition은 core tensor와 원래 tensor보다 low rank인 sub tensor들의 곱으로 나타내는 것
tucker decomposition은 해석보다는 compression에 유용하다
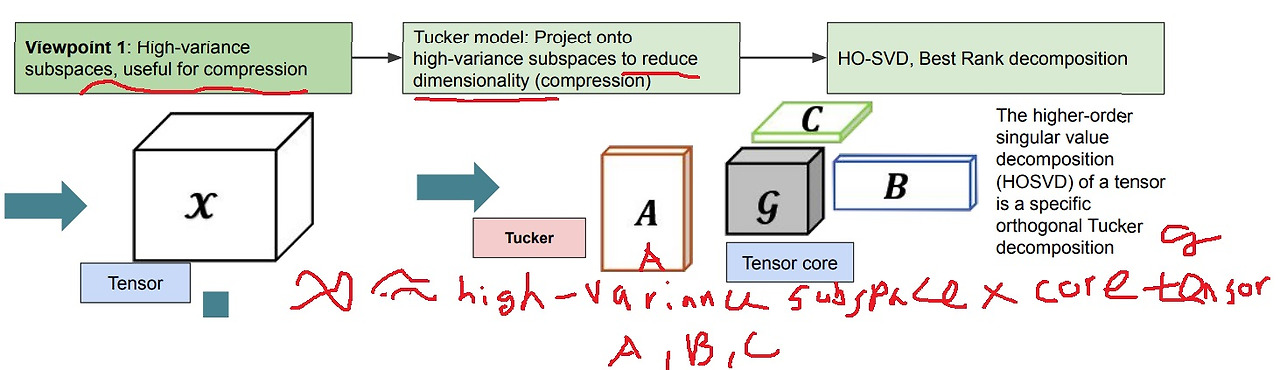
tucker decomposition은 dimension을 줄여 compression을 하기 위해 high variance subspace로 projection한 것이다.
8. CP decomposition의 활용
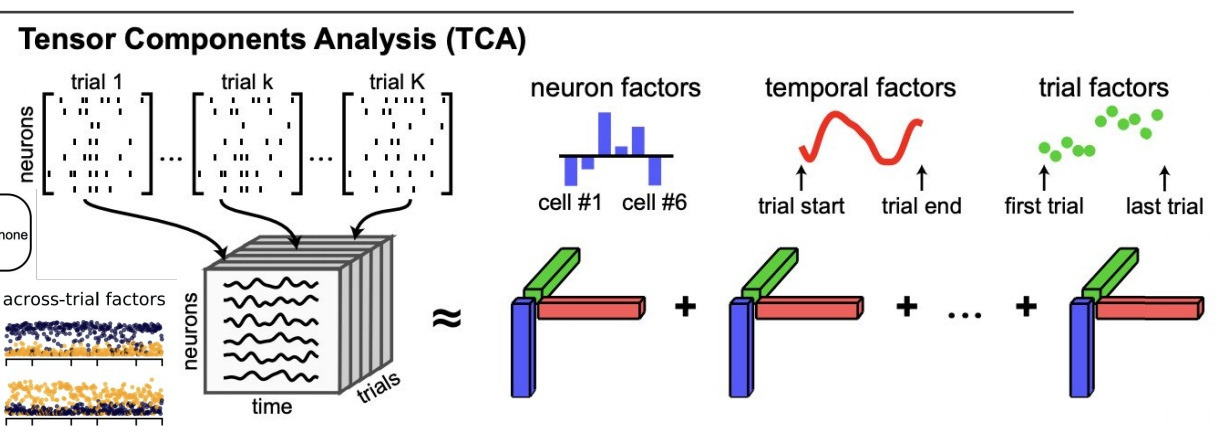
쥐에 기계장치를 꽂아 미로를 찾게하는 실험에서
neuron factor, time factor, trial factor로 데이터를 모델링하면 3차원 tensor로 modeling가능

이 때 각 factor가 어떻게 영향을 미치는지 알고 싶으면 tensor를 CP decomposition을 통해 분해해서 분석할 수 있다고함
neural network의 weight decomposition이 아니라 주어진 데이터를 decomposition하여 feature를 분석하는거라고 볼 수 있을까
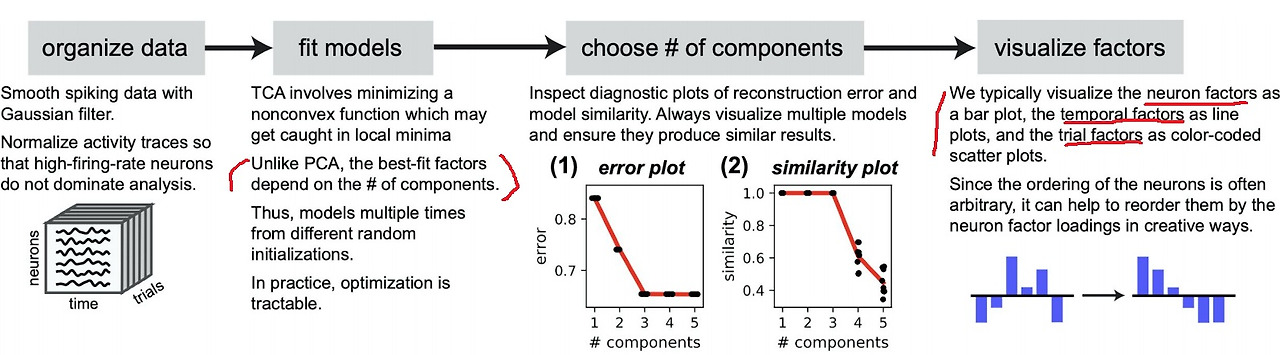
구체적으로 데이터를 구성하고 데이터를 model에 fitting한 다음에 PCA에서 component 수를 결정하듯이
분석하여 주요 component를 결정하고 결정한 component 수에 따른 factor를 visualize하여 분석
9. tensor decomposition은 유일한 해를 가지는가?
주어진 tensor를 유일하게 어떤 tensor들의 곱이나 합으로 분해할 수 있을까?
많은 경우 유일하게 분해하기 어렵다고 볼 수 있는데
예를 들어 full rank decomposition을 하더라도 스칼라배를 해서 A=KL을 해도 A=(1/2)K * 2L 여러가지 만들 수 있어서
유일하다고 보기는 어렵다
이론적으로 CP decomposition이나 Tucker decomposition은 non-convex optimization 문제로 유일한 해를 갖지는 않는다
실험적으로 real-life image data에 대해 CP decomposition은 유일한 해를 갖지 않지만
Tucker decomposition은 global unique solution을 가질 수 있는 경우가 있다는 것을 밝힌 논문이 있다
'딥러닝 > light weight modeling' 카테고리의 다른 글
| hardware-software codesign 개념 (0) | 2024.08.27 |
|---|---|
| AutoML의 개념 알아보기 (0) | 2024.08.23 |
| network pruning이란 (0) | 2024.08.18 |
| MobileNet과 network decoupling (0) | 2024.08.18 |
| tensor decomposition 간단한 설명 (0) | 2024.08.17 |

