https://atcoder.jp/contests/abc362/tasks/abc362_c
C - Sum = 0
AtCoder is a programming contest site for anyone from beginners to experts. We hold weekly programming contests online.
atcoder.jp
n개의 구간 (Li,Ri)가 주어질때, 이 구간들 각각에서 정수 Xi를 하나 골라 n개 합쳐서 0을 만들 수 있는지?
그렇다면 그러한 정수 배열을 하나 찾는 문제
먼저 그러한 정수 배열이 존재하는지 알 수 있을까?
이것부터 어렵더라고 근데 생각보다 간단했다
$$L_{1} <= X_{1} <= R_{1}$$
$$L_{2} <= X_{2} <= R_{2}$$
...
$$L_{n} <= X_{n} <= R_{n}$$
이들을 합해도 부등식이 유지되므로,
$$\sum_{i = 1}^{n} L_{i} <= \sum_{i = 1}^{n} X_{i} <= \sum_{i = 1}^{n} R_{i}$$
따라서, $\sum_{i = 1}^{n} L_{i} <= 0 <= \sum_{i = 1}^{n} R_{i}$여야 그러한 정수 배열 X가 존재한다
그러면 이제 어떻게 X를 찾을 수 있을까가 더 어려운 문제다
모든 i = 1,2,3...,n에 대해 $X_{i} = L_{i}$으로 초기화해두면 반드시 $\sum_{i = 1}^{n} X_{i} <= 0$이다.
이 상태에서 i = 1,2,3...,n에 대해 Li,Ri를 순회하면서, Xi < Ri이고 $\sum_{i=1}^{n} X_{i} < 0$이면,
Xi가 Ri가 될때까지 가능한만큼 Xi를 1씩 증가시키면 된다
근데 1씩 증가시키기에는 Li와 Ri가 10^18차이라 시간이 부족하다
현재 $\sum_{i = 1}^{n} X_{i}$이고 이것을 0으로 만들려면 $D = - \sum_{i = 1}^{n} X_{i}$만큼 상승시켜야한다.
매 구간마다 $X_{i}$는 최대 $R_{i} - L_{i}$ 올릴 수 있는데, 올려도 0이 안된다면 이 최댓값만큼 올리면 된다.
근데 이 최댓값만큼 올리면 0을 넘을 수 있는데 그러면 남은 양인 $- \sum_{i=1}^{n} X_{i}$만큼 올리면 된다.
즉 $R_{i} - L_{i}$와 $- \sum_{i=1}^{n} X_{i}$중 더 작은 값만큼 올리면 된다.
그리고 이렇게 올린 양만큼, $- \sum_{i=1}^{n} X_{i}$를 갱신시켜주면 된다
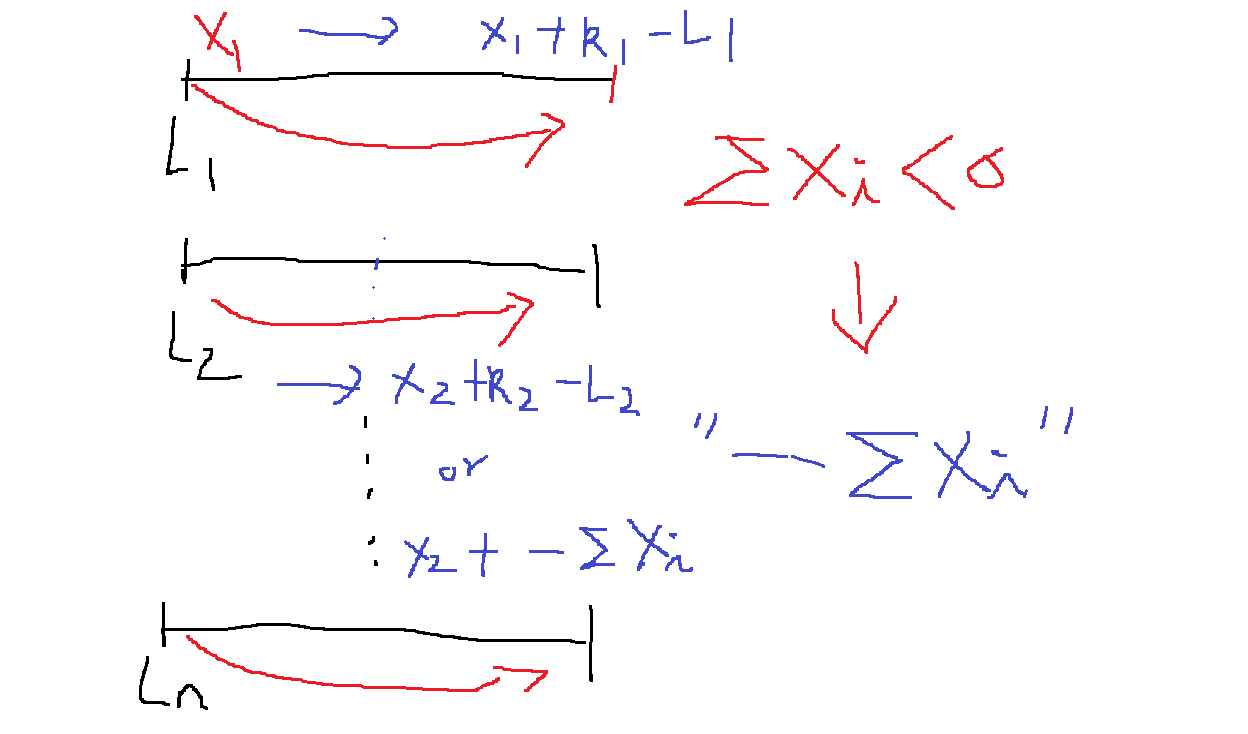
#n개의 구간 (l,r) 사이 정수를 하나씩 골라 합해서 0이 될 수 있는가?
from sys import stdin
n = int(stdin.readline())
L = 0
R = 0
interval = []
result = []
for _ in range(n):
l,r = map(int,stdin.readline().split())
interval.append((l,r))
result.append(l)
L += l
R += r
#l의 합 <= 0 <= R의 합이면, X배열을 찾을 수 있다
if L <= 0 and R >= 0:
print('Yes')
#최초 Xi들을 Li로 초기화(result)
#올려야하는 양은 -L만큼(Li들의 합)
diff = -L
for i in range(n):
l,r = interval[i]
#각 구간마다 Xi는 r-l만큼 최대로 올리거나,
#diff만큼 올리거나 할 수 있다
incre = min(diff,r-l)
result[i] += incre
diff -= incre
#올려야하는 양 diff가 0이 되면 합이 전부 0이 된다는 뜻
if diff == 0:
break
print(*result)
else:
print('No')
'알고리즘 > 애드 혹 알고리즘' 카테고리의 다른 글
| 맨 위 정수가 주어질때, 아래 두 수의 합이 위 정수가 되는 피라미드 만들기 (0) | 2024.09.06 |
|---|---|
| 특정한 정점들을 반드시 포함하는 최소 정점 트리 만들기 - list말고 반드시 set을 사용해야하는 경우 (0) | 2024.08.31 |
| n,m이 매우 클 때 (a1a2a3...an)/(b1b2b3...bm) 분수를 계산하는 마법같은 방법 (0) | 2024.07.25 |
| n번째로 작은 팰린드롬 수를 찾는 놀라운 방법 (0) | 2024.07.23 |
| 문자열 수를 10진법으로 바꾸는 테크닉 - 배열에서 모든 가능한 순서쌍의 두 수를 이어붙여 만든 수의 합 (0) | 2024.06.11 |

