neural network의 weight나 activation을 연속적으로 정밀하게 미세한 값으로 표현하는 것보다
정밀도가 떨어지더라도 sparse하게 드문드문 떨어지는 덩어리 quantization으로 표현
1. 왜 하는가?
가장 중요한 부분은 training을 더 빠르게 하기위함보다는 inference 과정에서 속도를 빠르게 하고 싶어서 quantization을 하는 것
model size가 작아짐
32bit의 $2^{32}$에서 16bit로 $2^{16}$으로 8bit에서 $2^{8}$로 절반씩 표현능력과 size가 감소하나
그만큼 메모리양을 절약할 수 있음
저장된 데이터를 얼마나 읽어올 수 있는지 memory bandwidth의 필요량을 줄일 수 있다?
이게 무슨 말인지 생각해봤는데 큰 size 32bit짜리는 최소한 32bit를 한번에 불러올 수 있는 수준의 memory bandwidth를 가진 memory가 필요한데
8bit로 줄이면 1/4의 memory bandwidth를 가진 memory가 있으면 된다 이런 느낌인듯?
on device에서는 32bit float보다 8bit int가 계산이 더 빠르다고함
2. 예시로 이해하는 quantization 방법
y축 위에 연속적으로 표현된 실수를 3bit로 quantization하여 표현하려면
$2^{3} = 8$이니까 -4부터 3까지 8덩어리로 표현하면 된다(n bit이면 $-2^{n-1}$ , $2^{n-1}-1$까지 표현 가능)

-4~3까지 연속적으로 표현한 실수를 3bit quantization하면
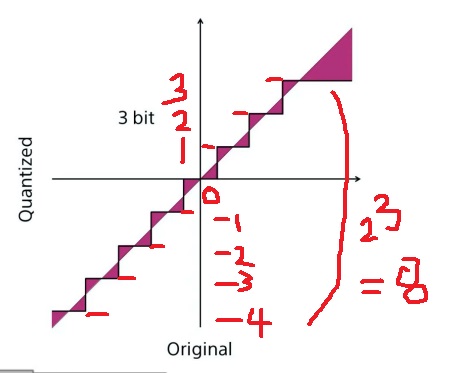
[-4,3]까지 실수를 3bit quantization하여 8덩어리로 표현함
3. lossy conversion
float32에서 int8로 quantization을 하면 int8이 표현하지 못하는 것이 많을 수 있다
int8은 255개의 채널을 가지므로 float32의 작은 범위를 int8로 mapping하면 정보의 엄청난 손실이 일어나는 lossy conversion
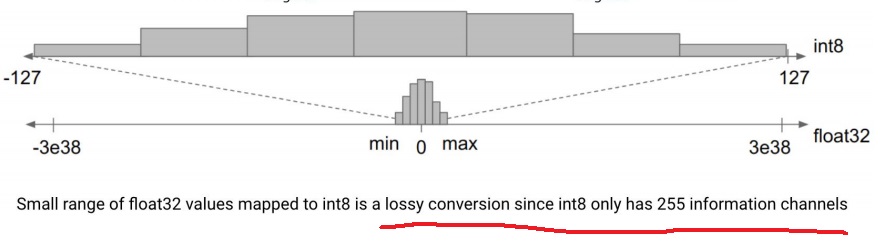
정보를 엄청 잃음에도 불구하고 이렇게 quantization하는 이유는 inference time에서 이득을 얻고자 하는 것
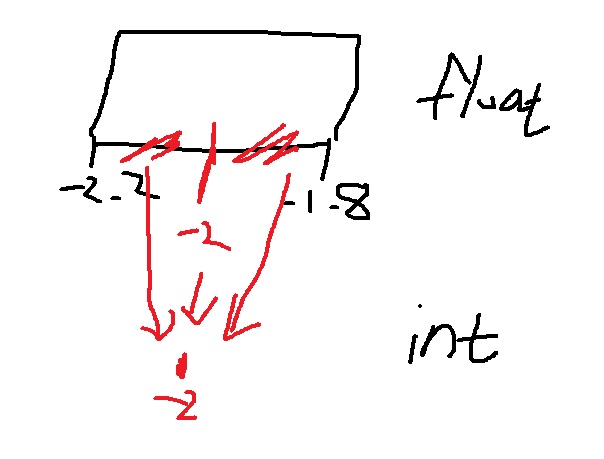
정보를 잃는 이유는 너무나 당연한 것이 [-2.2,-1.8]의 모든 실수를 -2로 mapping시키는데 -2.1 , -1.9 이런거 다 -2로 해서 무시해버리는데… 당연
4. quantization error
quantization을 하면 직선이 모든 실수를 나타내는데 정수만 취하는 계단함수로 바뀜
원래 직선과 계단함수가 이루는 면적들의 합이 quantization error라고 할 수 있음

색칠한 부분만큼 error가 생긴다고 할 수 있다
quantization을 해도 큰 차이가 없어보일수는 있지만..
A는 일반 floating point vector이고 B는 quantization해서 integer로 얻은 벡터

이렇게 아주 작아보이는 오차도 neural network는 그 parameter가 너무 많아 quantization을 쉽게 해버리면 그만큼 누적되어 문제가 생길 수 있다
저렇게 적게 quantization을 해도 문제 있을 수 있는데 엄청나게 큰 quantization을 쉽게 해버리면 상상도 못할 오차가 생기는거
5. low precision의 필요성
quantization의 주요 목적은 neural network에서 inference time의 이득을 보기 위해서다
기본적인 CNN만해도 들어가는 계산비용이 어마어마하다

위 그림에서 M이랑 N만 해도 128이어서 16354나 되는데 거기에 몇개 곱해진다면…?
아무리 요새 컴퓨팅 파워가 좋다고해도 network 복잡도가 상상할 수 없을 정도로 커지는 시대에 도저히 감당이 안됨
그래서 precision을 낮추고서 정보를 잃는 대가를 지불하고서라도 계산비용의 이득을 보고 싶은 것임
6. affine transformation
모든 x,y ∈ X에 대하여 $m_{f}(x-y) = f(x) - f(y)$를 만족시키는 linear mapping $m_{f}$:V → W가 존재한다면
linear mapping f:X→ Z를 affine transformation이라고 부른다
euclidean space는 affine space의 특별한 형태
transformation이 점은 점으로 선은 선으로 평면은 평면으로 보내며 평행선의 길이비를 유지함
평행선은 변환 후에도 여전히 평행
길이 비는 보존해야하지만 선 사이의 각이나 점 사이의 길이를 반드시 보존할 필요는 없다.
전체적인 모양은 유지하고 크기만 키우거나 줄이는 변환
7. 딥러닝에서 affine transform
딥러닝에서는 weight sum에 bias를 더하고 activation을 한 것이 affine transformation

데이터 x의 차원은 그대로 유지하면서 단순한 scale을 키우는 변환
8. affine quantization이란
딥러닝에서 affine transformation으로 예측값을 구하는 과정 중간 중간에 floating point를 integer로 바꿔서 연산을 함

위 그림에서 보면 input 들어갈 때는 floating이었다가 int8로 바꿔서 합치고 int32로 activation했다가.. 나중에 float16으로 바꾸고
'딥러닝 > light weight modeling' 카테고리의 다른 글
| Efficient Architecture design이란 (0) | 2024.08.14 |
|---|---|
| 왜 경량화인가? 딥러닝 모델의 경량화가 필요한 이유 (0) | 2024.08.14 |
| 값싼 비용으로 최대 효율을 낼 수 있을까 - lottery ticket hypothesis (0) | 2022.12.31 |
| iterative pruning의 여러가지 변형 버전 알아보기 (0) | 2022.11.14 |
| pruning을 하는 여러가지 방법들 (0) | 2022.11.12 |

