1. 구조
binary indexed tree는 이름에서부터 2진법 인덱스 구조를 이용해서 구간 합 문제를 효과적으로 처리하기 위한 자료구조
point update, range sum을 효과적으로 처리하기 위한 자료구조
다음 그림이 binary indexed tree의 구조를 잘 보여주고 있다.
1) zero index가 아니라 binary indexed tree에서는 편의상 one index로 바꿔서 생각함
2) 데이터가 N개면 tree의 크기도 N이다.

3) tree의 각 index에는 어떤 값들이 저장되어 있는가?
1번 index에는 0번째 원소 1이 있고, 2번 index에는 0번 + 1번째 원소의 합 1+3 = 4가 저장
마찬가지로 3번 index에는 2번째 원소 11이 저장
4번 index에는 0,1,2,3번째 원소들의 합 1+3+11+6 = 21이 저장..
빨간색 화살표대로 저장되어 있는 자료구조
------------------------------------------------------------------------------------------------------------------------------------------------------------
2. 0이 아닌 마지막 비트
정수는 컴퓨터에서 내부적으로 2진수로 저장하는데
예를 들어 정수 7은 2진법으로 나타내면 '0000111'이다.
-7은 7의 모든 bit를 뒤집어서 '1111000'으로 하고 1을 더해준 '1111001'이다.
이를 이용해서 정수 K의 0이 아닌 마지막 비트는 K & -K를 하면 바로 구할 수 있다.
예를 들어 몇가지를 생각해보자.
정수 4는 '0000100'이다. 0이 아닌 마지막 비트는 '100' 부분의 4이다.
-4는 '1111011'에서 1을 더한 '1111100'이다.
'0000100' & '1111100'을 하면 '0000100'이다. 이는 4와 동일하다.
다른 예로 6은 '0000110'인데, 0이 아닌 마지막 비트는 '10'의 2이다.
-6은 '1111001'에서 1을 더한 '1111010'이다.
'0000110' & '1111010'은 '0000010'으로 2가 나온다.
3. binary indexed tree의 핵심 특징
binary indexed tree의 각 인덱스 i의 0이 아닌 마지막 비트가 k이면, 해당 index는 0~k-1번째 원소까지의 합을 저장한다.

예를 들어 4는 0이 아닌 마지막 비트가 4여서 0,1,2,3번째 4개 원소의 합을 저장한다.
6은 0이 아닌 마지막 비트가 2여서 4,5번째 2개 원소의 합을 저장한다.
7은 0이 아닌 마지막 비트가 1이여서 6번째 1개 원소의 합을 저장하고 있다.
4. point update
특정 원소의 값을 바꾼다면?
예를 들어 다음 그림에서 3번째 원소의 값을 바꾼다면?
그러면 3번째 원소를 포함하고 있는 1~4번째 원소 합(4번째 index), 1~8번째 원소 합(8번 index), 1~16번째 원소 합(16번)
도 모두 바꿔줘야한다.
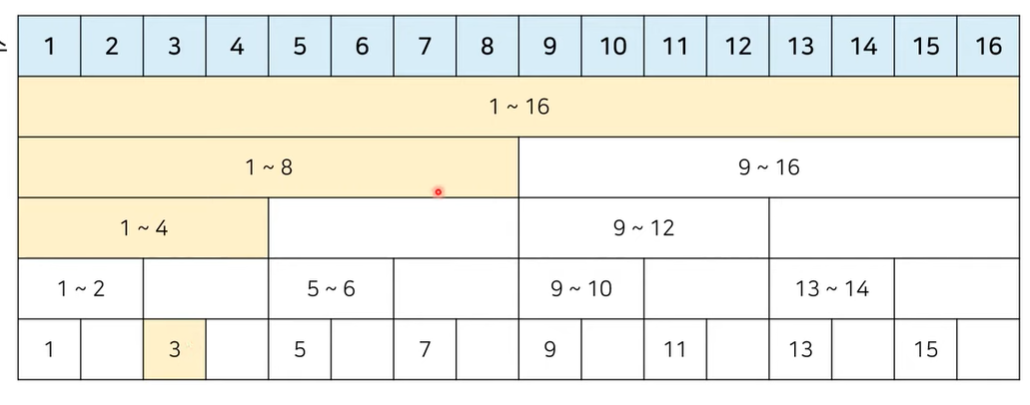
이 때는 놀랍게도 바꾸고자하는 원소의 index의 0이 아닌 마지막 비트 만큼 더해가면서 모든 index들의 원소를 바꾸면 된다.
여기서는 3번 index의 0이 아닌 마지막 비트를 구하면 1인데,
3번 index를 바꾸고 >>> 3번 index + 1 = 4번 index의 값을 바꾼다
>> 4번 index의 0이 아닌 마지막 비트는 4이고, 4를 더한 8번 index의 원소 값을 바꾼다.
>> 8번 index의 0이 아닌 마지막 비트는 8이고 8을 더한 16번 index의 원소 값을 바꾼다.
따라서 3 > 4 > 8 > 16번 index의 원소들에 value만큼 더해주면 된다.
최악의 경우에도 바꾸는 시간은 O(logN)이다.

알고리즘 그대로 구현하면 다음과 같다
#i번째 수에 value만큼 더하는 함수
def point_update(i,value):
#현재 i에 value를 더하고,
#0이 아닌 마지막 비트 (i & -i)만큼 이동하여 그곳에 value를 더해줌
#i가 마지막 인덱스를 넘어가면 종료
while i <= n:
tree[i] += value
i += (i & -i)
5. range sum
1번 원소부터 n번 index까지 원소의 누적합을 구하는 방법?
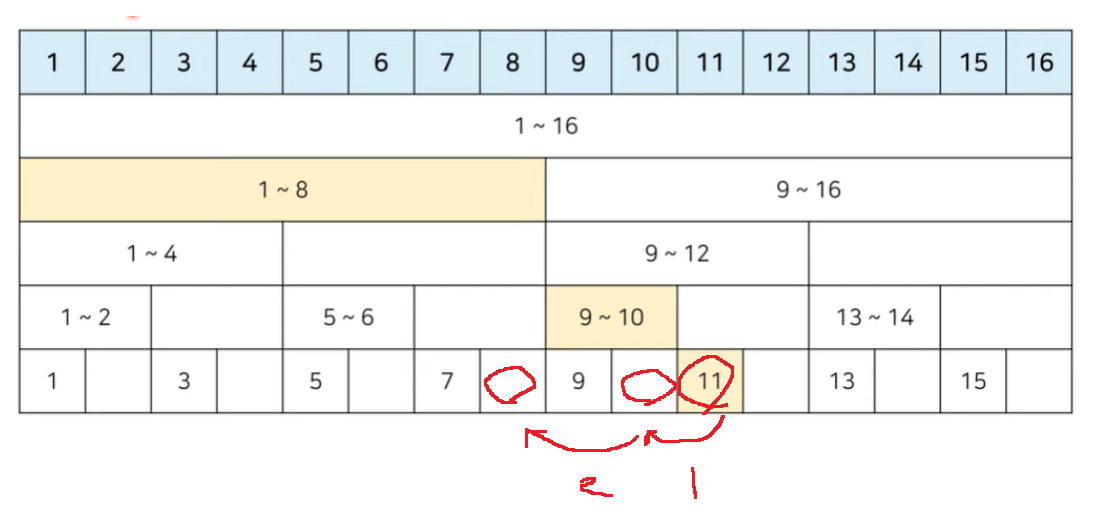
예를 들어 1번~11번 원소의 합을 구하고 싶다.
그러면 tree 구조 상 1~8번까지 누적합 + 9~10 누적합 + 11번, 3개 원소 합을 구하면 된다.

놀랍게도 11번부터 시작해서 해당 index의 0이 아닌 마지막 비트만큼 빼가면서 해당 위치의 원소들을 합하면 된다.
11번 index 원소를 더해주고, 11은 0이 아닌 마지막 비트가 1이므로
>> 1을 뺀 10번 index의 원소를 더해준다. 10은 0이 아닌 마지막 비트가 2이므로
>> 2를 뺀 8번 index의 원소를 더해준다.
따라서 11번 + 10번 + 8번 원소의 합을 구하면 된다.
이렇게 하면 최악의 경우에도 O(logN)의 연산으로 1~N번까지 누적합을 구할 수 있다.
알고리즘 그대로 구현하면 다음과 같다
#1~i번 index까지 누적합을 구하는 함수
def range_sum(i):
result = 0
#현재 i번의 값을 더해주고
#0이 아닌 마지막 비트 (i & -i)만큼 빼주면서 다음 i로 이동
#i가 첫번째 인덱스보다 밑으로 넘어가면 종료
while i > 0:
result += tree[i]
i -= (i & -i)
return result
6. 연습문제
2042번: 구간 합 구하기
첫째 줄에 수의 개수 N(1 ≤ N ≤ 1,000,000)과 M(1 ≤ M ≤ 10,000), K(1 ≤ K ≤ 10,000) 가 주어진다. M은 수의 변경이 일어나는 횟수이고, K는 구간의 합을 구하는 횟수이다. 그리고 둘째 줄부터 N+1번째 줄
www.acmicpc.net
7. 풀이
1번 쿼리가 주어지면 b번째 원소를 c로 바꾸고, 2번 쿼리가 주어지면 b번부터 c번까지 누적합을 구하는 문제
point update, range sum query의 경우 fenwick tree를 이용하면 일반 segment tree보다 간단하게 해결할 수 있다.
먼저 binary indexed tree를 구성해야하는데, tree의 index 번호는 1번부터 n번까지로 하는게 좋다.
그래서 tree = [0] * (n+1)로 초기화하고, 현재 모든 tree에는 0으로 되어 있다.
이는 사실 원래 array가 [0,0,0,0,...,0]인 상태에서 만든 tree와 같다.
이 상태에서 각 i번 인덱스에 A[i]를 더해주면 [A[0],A[1],..., A[n-1]]이다.
이 과정은 i번째 index에 A[i]를 더해준 것과 같다.
따라서 tree에 A[i]의 원소를 넣을려면 i+1번째를 A[i]로 update하면 된다(zero index 기준)
A배열을 one index로 생각한다면 i번째를 A[i]로 update하면 된다
#binary indexed tree를 만드는 방법
#1번부터 n번 index
tree = [0]*(n+1)
for i in range(1,n+1):
a = int(input())
A.append(a)
point_update(i,a) #i번째 index를 a로 바꿔줌
여기서 A배열은 zero index로 생각하고 tree는 one index로 생각하다보니
"i번째 index를 a로 바꿔줌"이 헷갈릴 수 있는데...
그냥 A[0] = 0로 하고 A배열도 one index로 생각한다면 헷갈릴게 없다.
그러면 i번째 원소는 무조건 A[i]이다.
아무튼 b번째 원소를 c로 바꾸는 쿼리는 어떻게 할까?
point_update는 i번째 수에 value를 더해주는 함수이다.
#i번째 수에 value만큼 더하는 함수
def point_update(i,value):
#현재 i에 value를 더하고,
#0이 아닌 마지막 비트 (i & -i)만큼 이동하여 그곳에 value를 더해줌
#i가 마지막 인덱스를 넘어가면 종료
while i <= n:
tree[i] += value
i += (i & -i)
하지만 b번째 원소를 c로 바꾸는 것은 A[b] = k이면, A[b] = c로 바꾸는 것이다.
즉, A[b]에 c - k를 더해주면 A[b] = c가 된다.
for _ in range(m+k):
a,b,c = map(int,input().split())
if a == 1:
#b번째 원소를 c로 바꾼다
#A[b-1] = k이면, A[b-1] = c로 바꿀려면?
#A[b-1]에 c-k를 더한다.
point_update(b,c-A[b-1])
A[b-1] = c
2번째 쿼리인 b번째 원소부터 c번째 원소까지의 합은 어떻게 구할까?
range_sum(i)는 1번부터 i번까지 합이다.
#1~i번 index까지 누적합을 구하는 함수
def range_sum(i):
result = 0
#현재 i번의 값을 더해주고
#0이 아닌 마지막 비트 (i & -i)만큼 빼주면서 다음 i로 이동
#i가 첫번째 인덱스보다 밑으로 넘어가면 종료
while i > 0:
result += tree[i]
i -= (i & -i)
return result
따라서 누적합 배열 이용할때처럼 1번부터 c번까지 합 - (1번부터 b-1번까지 합) = b~c번 구간합을 구하면 된다.
여기서 tree[0] = 0이므로, i = 0이면, 0이 나오니까 예외 처리는 신경쓰지 않아도 된다.
print(range_sum(c) - range_sum(b-1))
그래서 기본적인 point update, range sum fenwick tree는..
from sys import stdin
#i번째 수에 value만큼 더하는 함수
def point_update(i,value):
#현재 i에 value를 더하고,
#0이 아닌 마지막 비트 (i & -i)만큼 이동하여 그곳에 value를 더해줌
#i가 마지막 인덱스를 넘어가면 종료
while i <= n:
tree[i] += value
i += (i & -i)
#1~i번 index까지 누적합을 구하는 함수
def range_sum(i):
result = 0
#현재 i번의 값을 더해주고
#0이 아닌 마지막 비트 (i & -i)만큼 빼주면서 다음 i로 이동
#i가 첫번째 인덱스보다 밑으로 넘어가면 종료
while i > 0:
result += tree[i]
i -= (i & -i)
return result
n,m,k = map(int,stdin.readline().split())
A = [0]
#binary indexed tree를 만드는 방법
#1번부터 n번 index
tree = [0]*(n+1)
for i in range(1,n+1):
a = int(stdin.readline())
A.append(a)
point_update(i,a) #i번째 index를 a로 바꿔줌
for _ in range(m+k):
a,b,c = map(int,stdin.readline().split())
if a == 1:
#b번째 원소를 c로 바꾼다
#A[b-1] = k이면, A[b-1] = c로 바꿀려면?
#A[b-1]에 c-k를 더한다.
point_update(b,c-A[b])
A[b] = c
else:
print(range_sum(c) - range_sum(b-1))
'알고리즘 > 세그먼트 트리' 카테고리의 다른 글
| 세그먼트 트리 응용단계 - 이분탐색과 콜라보1 (0) | 2023.05.09 |
|---|---|
| 세그먼트 트리 기본문제로 연습하며 재활(반복문, 재귀 연습) (0) | 2023.05.05 |
| 반복문으로 구현하는 세그먼트 트리(iterative segment tree) 배우기 (0) | 2023.05.04 |
| 세그먼트 트리 응용 - 2개의 쿼리를 동시에 수행할 수 있는 2차원 세그먼트 트리 (0) | 2022.12.15 |
| 세그먼트 트리 응용 - XOR 연산을 수행하는 트리 (0) | 2022.12.15 |

