1. exhaustive search
decoding의 매 스텝마다 모든 가능한 경우에 대해 확률분포를 따져보겠다는 것이다.
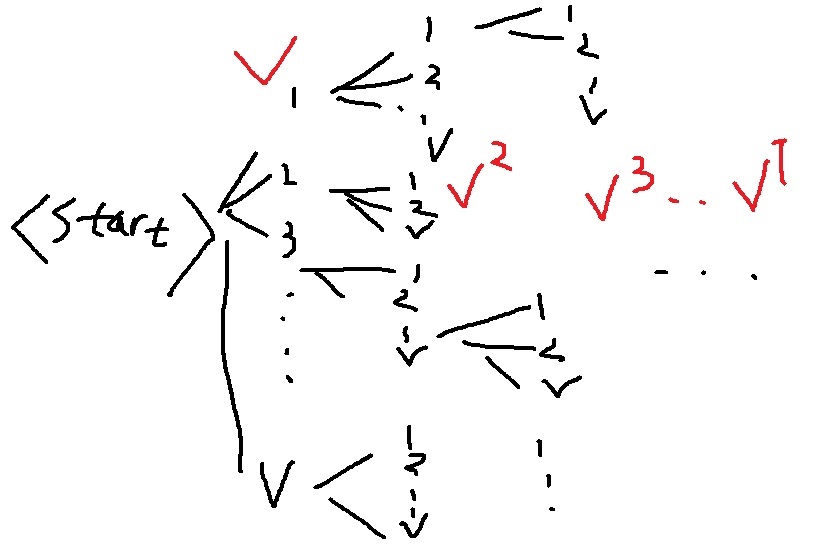
모든 가능한 경로에 대해 확률을 계산하여 최종적으로 가장 확률이 높은 1가지를 선택한다
근데 이제 보면 알겠지만 계산비용이 $O(V^{T})$로 T가 조금만 커져도 말도 안되게 커진다
참고로 greedy decoding은 매 스텝마다 가장 확률이 높은 1가지만 뽑으니까

2. beam search
greedy는 계산이 쉽지만 최적을 항상 보장하지 않는다는 점,
exhaustive search는 계산 비용이 너무 많이 든다는 점에서 중간책을 선택하고 싶다는 것이다.
그렇다면 매 step마다 beam size=k개만 고려하겠다.
최종적으로 고려한 적절한 수의 후보들 중 가장 확률이 높은 후보를 선택하겠다.
beam size는 고려하는 대상의 개수로 보통 5~10을 선택한다고 한다.
각각의 완성된 후보를 completed hypothesis라고 한다.
각 스텝마다 나오는 hypothesis를 y1,y2,y3,....yt라고 한다면
완성된 hypothesis의 최종 score는 각 step마다 계산되는 로그확률 logP(yt|y1,y2,...,yt-1,x)의 총합으로 구해진다.

로그로 계산하는 이유는 곱연산을 합연산으로 바꿔주기 위해서 그렇다.
확률은 1보다 작으니까 계속 곱하면 컴퓨터연산은 쉽게 0으로 만들어버리니까
로그 안쓴 값을 최대화하나 로그 쓴 값을 최대화하나 동일하다
확률은 0과 1 사이여서 로그를 취하면 score는 음수인데 그래도 score가 클수록 확률이 크다
3. 예시로 이해하는 beam search
beam size=2인 경우를 생각해보자.
첫 스텝에서 vocab에서 가장 확률이 높은 두 단어를 뽑는다.
이들의 로그를 취한 값을 score로 계산하는 것
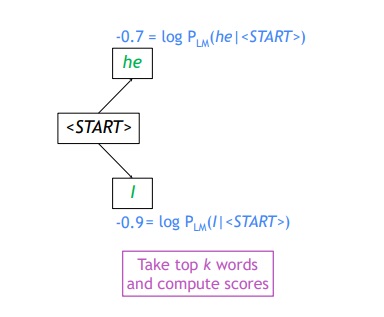
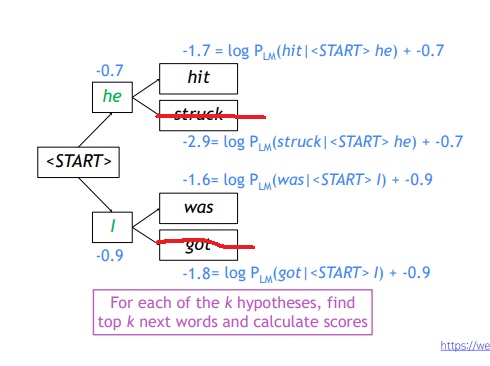
두번째 step에서 각 he와 i의 경우에서 2가지씩 확률이 가장 높은 단어를 뽑아내는 것이다.

각각의 score가 계산되는데 각 4가지 hypothesis의 score는 그 경로에 나타나는 모든 로그확률의 합으로 -1.7,-2.9,-1.6,-1.8이다.
예를 들어 he hit은 score가 -0.7 + -1.0 = -1.7을 가진다
근데 이제 이 4가지를 모두 고려하면서 각각에서 또 2가지씩 뽑느냐? 그것은 아니다.
4가지중 score가 가장 낮은 2가지는 없애면서 결국에는 매 step마다 k개를 항상 고려하게 된다.
확률이 낮은 2가지 struck, got는 제거함
2번째 step에서도 결국엔 2개만 고려함
위 step을 계속 반복해 나간다. 최종적으로 완성된 hypothesis에서 가장 확률이 높은 1가지만 선택하면 그것이 최종 번역문이다.

나는 근데 무조건 위 2가지 아래 2가지에서 나눠서 최대를 봐야하는줄 알았는데 아니네
4가지 중에서 2가지를 뽑는거네
-------------------------------------------------------------------------------------------
위 그림에서 보면 첫 스텝에서 he(-0.7), I(-0.9)
두번째 스텝에서 he hit(-1.7), I was(-1.6)
세번째 스텝에서 he hit me(-2.5), he hit a(-2.8)
네번째 스텝에서 he hit me with(-3.3), he hit a pie(-3.4)
다섯번째 스텝에서 he hit me with a(-3.7), he hit me with one(-4.3)
여섯번째 스텝에서 he hit me with a pie(-4.3), he hit me with a tart(-4.6)
......
-------------------------------------------------------------------------------------------
당연하지만 결과가 반드시 최적은 아니다.
그러나 고려한 경우의 수가 greedy보다는 많으니 더 최적에 가까울것이고 exhaustive search보다 계산비용에서 효율적이다.
'딥러닝 > NLP' 카테고리의 다른 글
| NLP에서 한 획을 그은 transformer은 왜 등장했는가 + bidirectional RNN의 특징 (0) | 2022.04.20 |
|---|---|
| length normalization을 이용한 beam search의 종료조건 (0) | 2022.04.19 |
| greedy decoding(greedy search)은 왜 최적이 아닐까? (0) | 2022.04.17 |
| attention 구조는 NLP를 어떻게 바꾸었는가 (0) | 2022.04.15 |
| teacher forcing 기법 (0) | 2022.04.15 |

